Download.vn Học tập Lớp 12
Bạn đang đọc: 14 tính chất thường gặp trong hình học phẳng
14 tính chất thường gặp trong hình học phẳng Tài liệu chinh phục hình học tọa độ phẳng
Giới thiệu Tải về Bình luận
- 1
Mua tài khoản Download Pro để trải nghiệm website Download.vn KHÔNG quảng cáo & tải File cực nhanh chỉ từ 79.000đ. Tìm hiểu thêm Mua ngay
14 tính chất thường gặp trong hình học phẳng là tài liệu giúp các bạn lớp 10 ôn lại các tính chất trong hình học phẳng và vận dụng nó làm các bài tập dựa theo những tính chất đó.
Tài liệu bao gồm 33 trang kèm theo 36 bài tập minh họa có hướng dẫn giải, vận dụng 14 tính chất đã trình bày để minh họa cụ thể. Hi vọng tài liệu sẽ giúp bạn có được kiến thức tổng hợp và cách nhìn nhận tốt nhất để tư duy giải thành công câu hình học tọa độ phẳng Oxy trong kỳ thi sắp tới. Sau đây là nội dung chi tiết mời các bạn cùng tham khảo và tải tài liệu tại đây.
14 tính chất thường gặp trong hình học phẳng
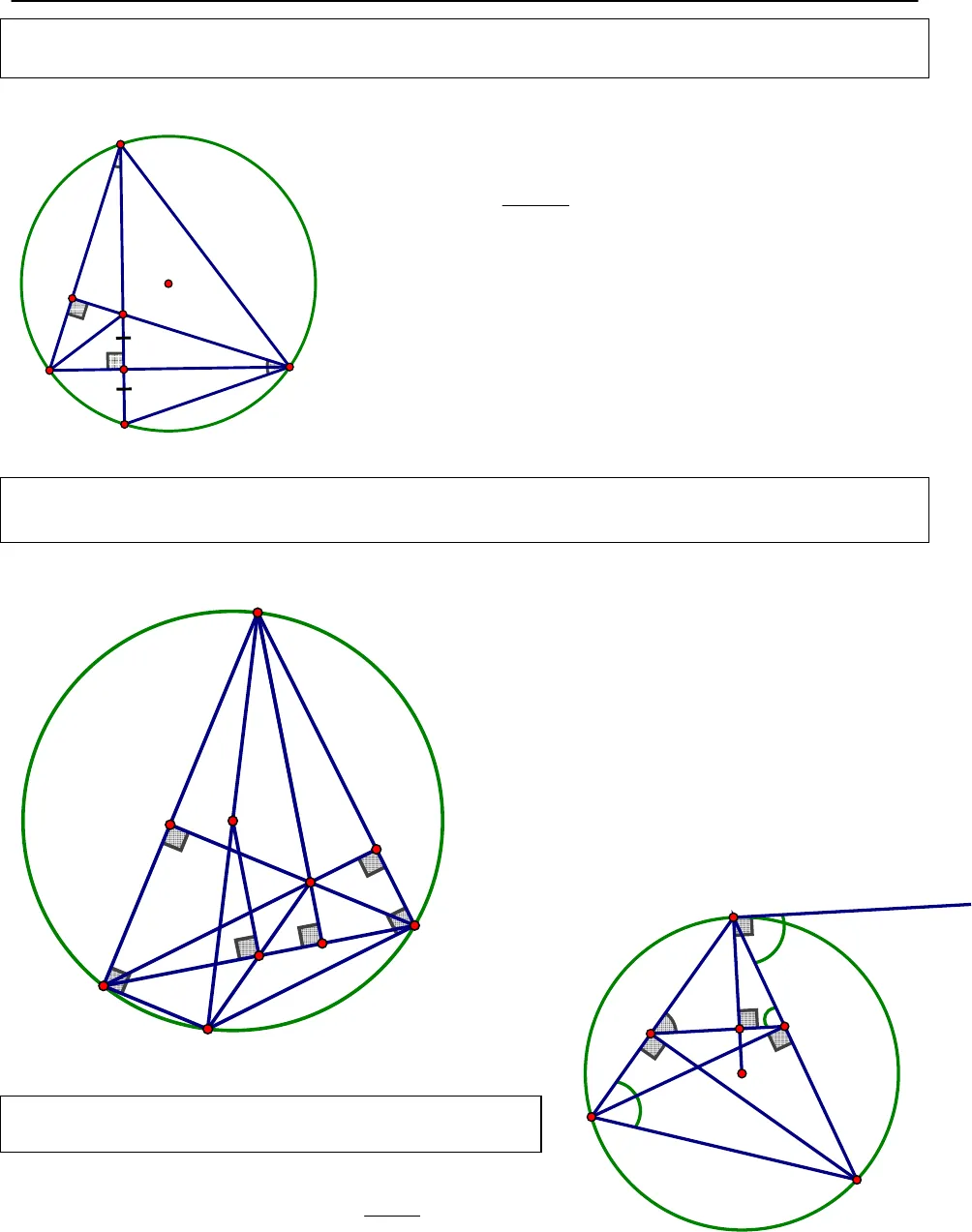CHINH PHỤCHÌNH HỌC TỌA ĐỘ PHẲNGTrang1Nguồn: http://www.toanmath.com/ Tính chất 1: Cho ABC∆nội tiếp đường tròn (O), H là trực tâm. Họi H’ là giao điểm của AH với đường tròn (O)H ‘⇒đối xứng với H qua BCHướng dẫn chứng minh:+ Ta có Gọi11A C====(cùng phụ vớiABC)+ Mà 12 1 2sdBH ‘A C C C2= == == == = ⇒⇒⇒⇒ ====HCH ‘⇒⇒⇒⇒ ∆∆∆∆cân tại C⇒⇒⇒⇒BC là trung trực của HH’H ‘⇒đối xứng với H qua BCTính chất 2: Cho ABC∆nội tiếp đường tròn (O), H là trực tâm, kẻ đường kính AA’, M là trungđiểm BC AH 2.OM⇒ = Hướng dẫn chứng minh:+ Ta có0ABA ‘ 90= (góc nội tiếp chắn nửa đường tròn tâm O) BA BA ‘⇒ ⊥, màBA CH BA ‘/ /CH⊥ ⇒(1).+ Chứng minh tương tự ta cũng cóCA ‘/ /BH(2)+ Từ (1) và (2)⇒tứ giác BHCA’ là hình bìnhhành, mà M là trung điểm đường chéo BC⇒M là trung điểm của đường chéo A’HOM⇒là đường trung bình của’H AH 2.OMAA∆ ⇒ = Tính chất 3: Cho ABC∆nội tiếp đường tròn (O), BHvà CK là 2 đường cao củaABC∆AO KH⇒ ⊥Hướng dẫn chứng minh:+ Kẻ tiếp tuyến AxsdACxAC ABC2⇒ = =+ MàABC AHK= (do tứ giá KHCB nội tiếp)xAC AHK⇒ = , mà 2 góc này ở vị trí so le trong/ /HKAx⇒+ Lại cóAx AO⊥(do Ax là tiếp tuyến)AO HK⇒ ⊥O211H’CBAHKHOxCBAMA’CBAOH
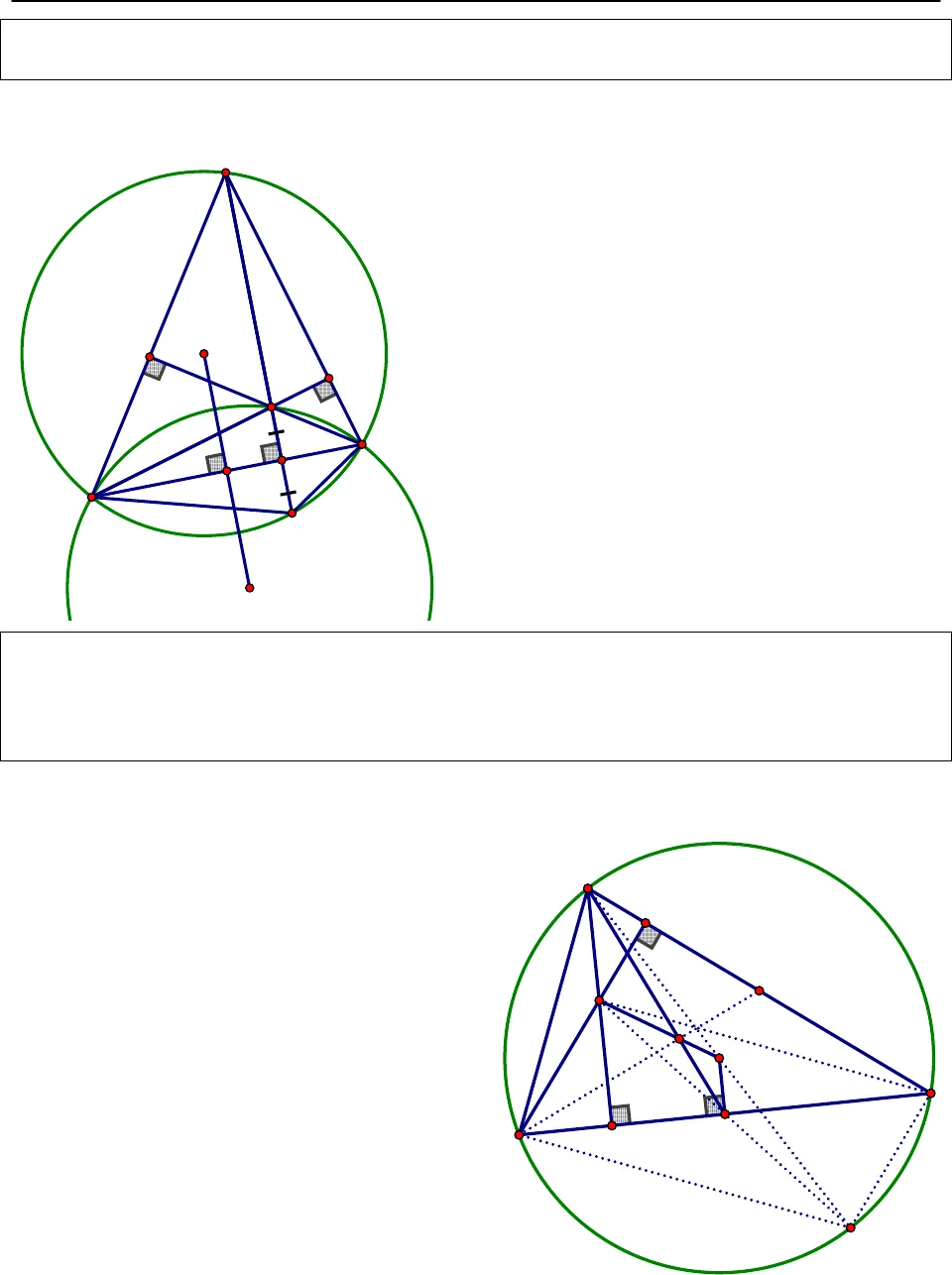CHINH PHỤCHÌNH HỌC TỌA ĐỘ PHẲNGTrang2Nguồn: http://www.toanmath.com/ Tính chất 4: Cho ABC∆nội tiếp đường tròn (O), H là trực tâm, gọi I là tâm đường tròn ngoạitiếp HBC∆ ⇒O và I đối xứng nhau qua BC.Hướng dẫn chứng minh:+ Gọi H’ là giao điểm của AH với đường tròn (O)⇒tứ giác ACH’B nội tiếp đường tròn (O) ⇒Ođồng thời là tâm đường tròn ngoại tiếp BH ‘C∆.+ Mặt khác H và H’ đối xứng nhau qua BC (tínhchất 1 đã chứng minh)HBC⇒ ∆đối xứng vớiH ‘BC∆qua BC, mà O, I lần lượt là tâm đườngtròn ngoại tiếpH ‘BC∆vàHBC∆I⇒và O đốixứng nhau qua BC.Tính chất 5: (Đường thẳng Ơ – le) Cho ABC∆, gọi H, G, O lần lượt là trực tâm, trọng tâm vàtâm đường tròn ngoài tiếpABC∆. Khi đó ta có:1).OH OA OB OC= + + 2). 3 điểm O, G, H thẳng hàng vàOH 3.OG= Hướng dẫn chứng minh:1). Ta đã chứng minh đượcAH 2.OM= (đãchứng minh ở tính chất 2) + Ta có :OA OB OC OA 2.OM OA AH OH+ + = + = + = 2). Do G là trọng tâmABC∆OA OB OC 3.OG⇒ + + = OA 2.OM 3.OGOA AH 3.OGOH 3.OG⇒ + =⇒ + =⇒ = Vậy 3 điểm O, G, H thẳng hàng IH’CBAOHOA’CMBAHG
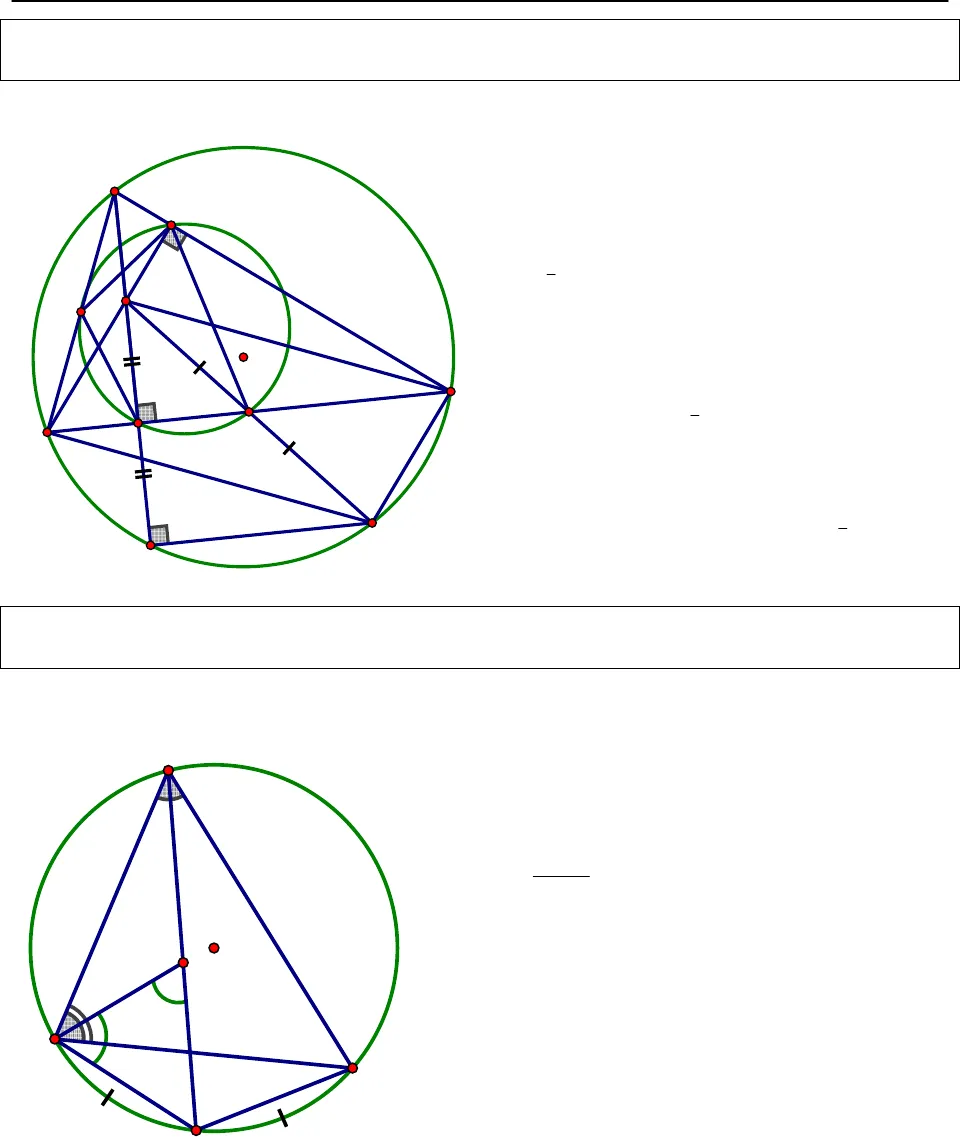CHINH PHỤCHÌNH HỌC TỌA ĐỘ PHẲNGTrang3Nguồn: http://www.toanmath.com/ Tính chất 6: Cho ABC∆nội tiếp đường tròn (O). Gọi D, E theo thứ tự là chân các đường cao từA, B. Các điểm M, N theo thứ tự là trung điểm BC và AB. ⇒tứ giác MEND nội tiếp.Hướng dẫn chứng minh:+ Ta có D là trung điểm HH’ (tính chất 1), Mlà trung điểm HA’ (do HCA’B là hình bìnhhành – tính chất 2). Như vậy ta có phép vị tự :1H;2(A ‘) MV ?H ‘) D ==+ Mà 2 điểm A’, H’ thuộc đường tròn ngoạitiếpABC∆⇒ 2 điểm M, D thuộc đườngtròn (C’) là ảnh của đường tròn (C) tâm Oqua phép vị tự 1H;2V (1)+ Chứng minh tương tự ta cũng có 2 điểm N,E thuộc đường tròn (C’) là ảnh của đườngtròn (C) tâm O qua phép vị tự1H;2V (2)+ Từ (1) và (2)⇒4 điểm D, M, E, N thuộcđường tròn (C’).Tính chất 7: Cho ABC∆, gọi O và I lần lượt là tâm đường tròn ngoại tiếp, tâm đường tròn nội tiếpABC∆, AI cắt đường tròn (O) tại DDB DI DC⇒ = =Hướng dẫn chứng minh:+ Ta có11 1I A B= +ɵ(do1Ilà góc ngoàiABI∆)+ Mà1 2B B=(Do BI là phân giácABC∆),1 2A A=(Do AI là phân giácABC∆), mà2 3sdBCA B2= =1 2 3I B B IBD IBD⇒ = + = ⇒ ∆ cântại DDI DB⇒ =(1)+ Ta lại có1 2A A=BD DC BD DC⇒ = ⇒ = (2)+ Từ (1) và (2)DB DI DC⇒ = =NEDH’OA’CMBAH132121IOCDBA