Download.vn Học tập Lớp 12

Bạn đang đọc: 1971 bài tập trắc nghiệm chuyên đề hàm số

1971 bài tập trắc nghiệm chuyên đề hàm số Bộ câu hỏi trắc nghiệm chuyên đề hàm số có đáp án

Giới thiệu Tải về Bình luận

• 1

Mua tài khoản Download Pro để trải nghiệm website Download.vn KHÔNG quảng cáo & tải File cực nhanh chỉ từ 79.000đ. Tìm hiểu thêm Mua ngay

Dưới đây Download.vn xin giới thiệu đến quý thầy cô và các em học sinh, đặc biệt là học sinh lớp 12 tài liệu 1971 bài tập trắc nghiệm chuyên đề hàm số.

Tài liệu gồm 272 trang tổng hợp 1971 bài tập trắc nghiệm chuyên đề hàm số mức độ cơ bản trong các đề thi thử THPT Quốc gia. Đây là tài liệu vô cùng hữu ích, giúp thầy cô giáo có thêm nhiều tư liệu ra đề thi cũng như ôn luyện cho các em. Đồng thời giúp các em học sinh luyện và nâng cao kỹ năng giải toán. Mời các bạn cùng tham khảo và tải tài liệu tại đây.

1971 bài tập trắc nghiệm chuyên đề hàm số

Câu 1. (THPT Chuyên Amsterdam – Hà Nội – 2017) Hàm số 3234yx x đạt cực tiểu tại điểm: A. 0x  B.2x  C.4x  D.0x và2xCâu 2. (THPT Chuyên Amsterdam – Hà Nội – 2017) Đồ thị hàm số 232xyxxcó bao nhiêu đường tiệm cận đứng: A. 0 B.1 C.2 D.3Câu 3. (THPT Chuyên Amsterdam – Hà Nội – 2017) Giả sử tiếp tuyến của đồ thị hàm số 322 6 18 1yx x x song song với đường thẳng ( ) : 12 0d xy có dạng là .y ax bKhi đó tổng của ablà:A. 15 B.27 C.12 D.11Câu 4. (THPT Chuyên Amsterdam – Hà Nội – 2017) Tìm GTLN và GTNN của hàm số 54 3551yx x x  trên 1; 2 ?A. 1;2 1;2min 10, max 2xxyy     B.1;2 1;2min 2, max 10xxyy    C. 1;2 1;2min 10, max 2xxyy     D.1;2 1;2min 7, max 1xxyy    Câu 5. (THPT Chuyên Amsterdam – Hà Nội – 2017) Hàm số 3234yx x đồng biến trên:A.  0; 2B. ( ; 0)và(2; )C. ( ;2) D.(0; )Câu 6. (THPT Chuyên Amsterdam – Hà Nội – 2017) Số điểm cực trị của đồ thị hàm số 12xyxlà: A. 0 B.1 C.2 D.3Câu 7. (THPT Chuyên Amsterdam – Hà Nội – 2017) Cho hàm số ()y fxcó bảng biến thiên như sau. Khẳng định nào dưới đây là đúng? A. Hàm số nghịch biến trên ( ;2). B. Hàm số đạt cực đại tại 3.x C. ( ) 0, .fx x  D. Hàm số đồng biến trên  0; 3.Câu 8. (THPT Chuyên Amsterdam – Hà Nội – 2017) Gọi giá trị lớn nhất và nhỏ nhất của hàm số 4221yx x trên đoạn 1; 2lần lượt là Mvàm. Khi đó, giá trị của.Mmlà:A. 2 B.46 C.23 D. Một số lớn hơn 46Câu 9. (THPT Chuyên Amsterdam – Hà Nội – 2017) Cho hàm số ()y fxcó đồ thị như hình vẽ. Khẳng định nào sau đây là đúng? A. max ( ) 3xfxB. Hàm số đồng biến trên khoảng ( ; 3).C. Giá trị cực tiểu của hàm số bằng 2.x−∞2−02+∞y′−0+0−0+y+∞030+∞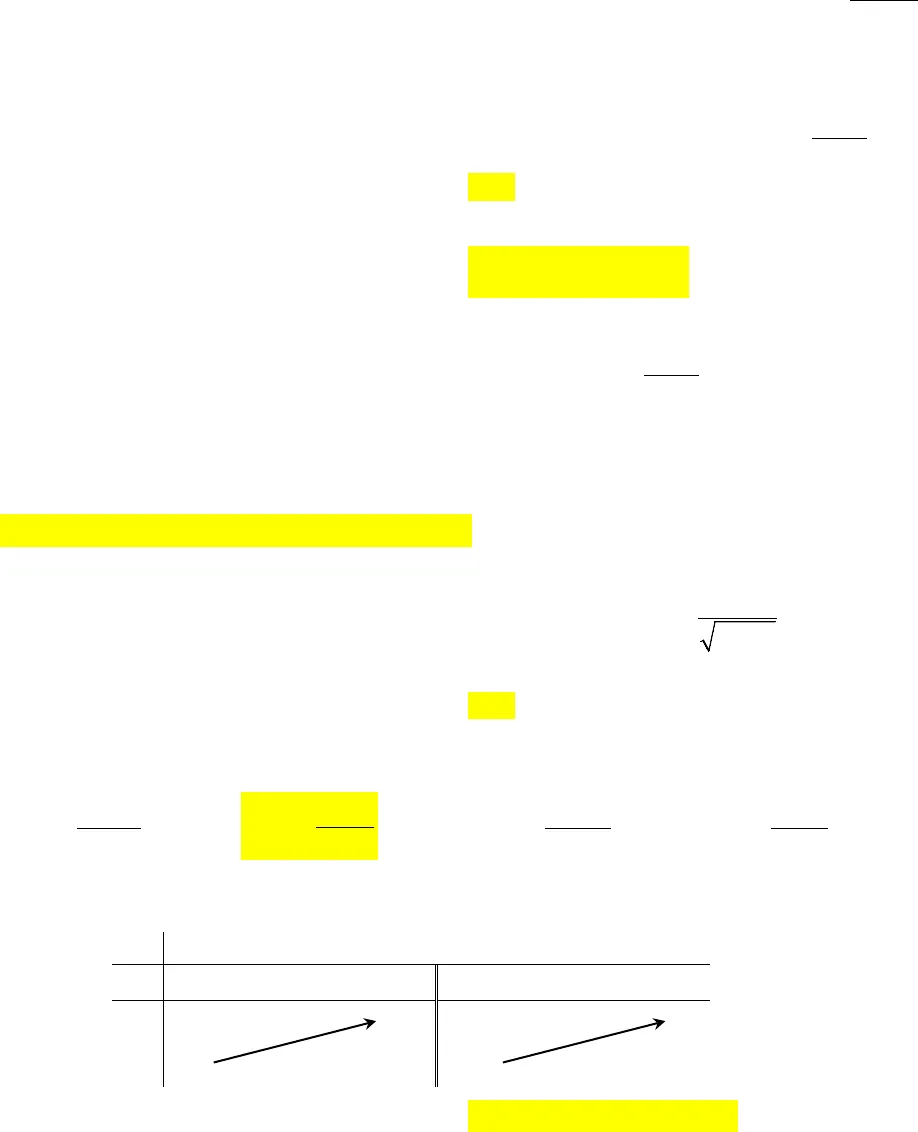D. 0;4min ( ) 1.xfxCâu 10. (THPT Chuyên Amsterdam – Hà Nội – 2017) Giá trị lớn nhất của hàm số 268()1xfxxtrên tập xác định của nó là: A. 15 B.27 C.12 D.11Câu 11. (THPT Chuyên Amsterdam – Hà Nội – 2017) Số tiệm cận của đồ thị hàm số 12xyxlà:A. 0 B.1 C.2 D.3Câu 12. (THPT Chuyên Amsterdam – Hà Nội – 2017) Hàm số 4223yxx  nghịch biến trên:A. ( ; 0) B.( ; 1) và 0; 1C. Tập số thực  D.(0; )Câu 13. (THPT Chuyên Amsterdam – Hà Nội – 2017) Cho hàm số 5.2yxKhẳng định nào dưới đây là đúng? A. Hàm số đồng biến trên {2}B. Hàm số nghịch biến trên ( 2; ) C. Hàm số nghịch biến trên ( ;2)và(2; )D. Hàm số nghịch biến trên Câu 14. (THPT Chuyên Amsterdam – Hà Nội – 2017) Đồ thị hàm số 21xyxcó bao nhiêu đường tiệm cận ngang: A. 0 B.1 C.2 D.3Câu 15. (THPT Chuyên Amsterdam – Hà Nội – 2017) Giao điểm của hai đường tiệm cận của đồ thị hàm số nào dưới đây nằm trên đường thẳng( ): ?dy xA. 213xyx B.41xyx C.212xyx D.13yxCâu 16. (THPT Chuyên Amsterdam – Hà Nội – 2017) Cho hàm số ()y fxcó bảng biến thiên như sau. Khẳng định nào dưới đây là đúng? A. Hàm số có tiệm cận đứng là 1.y  B. Hàm số không có cực trị.C. Hàm số có tiệm cận ngang là 2.x  D. Hàm số đồng biến trên .Câu 17. (THPT Chuyên Amsterdam – Hà Nội – 2017) Đồ thị bên là đồ thị của hàm số nào trong các hàm số sau? x−∞1+∞y′++y2+∞−∞2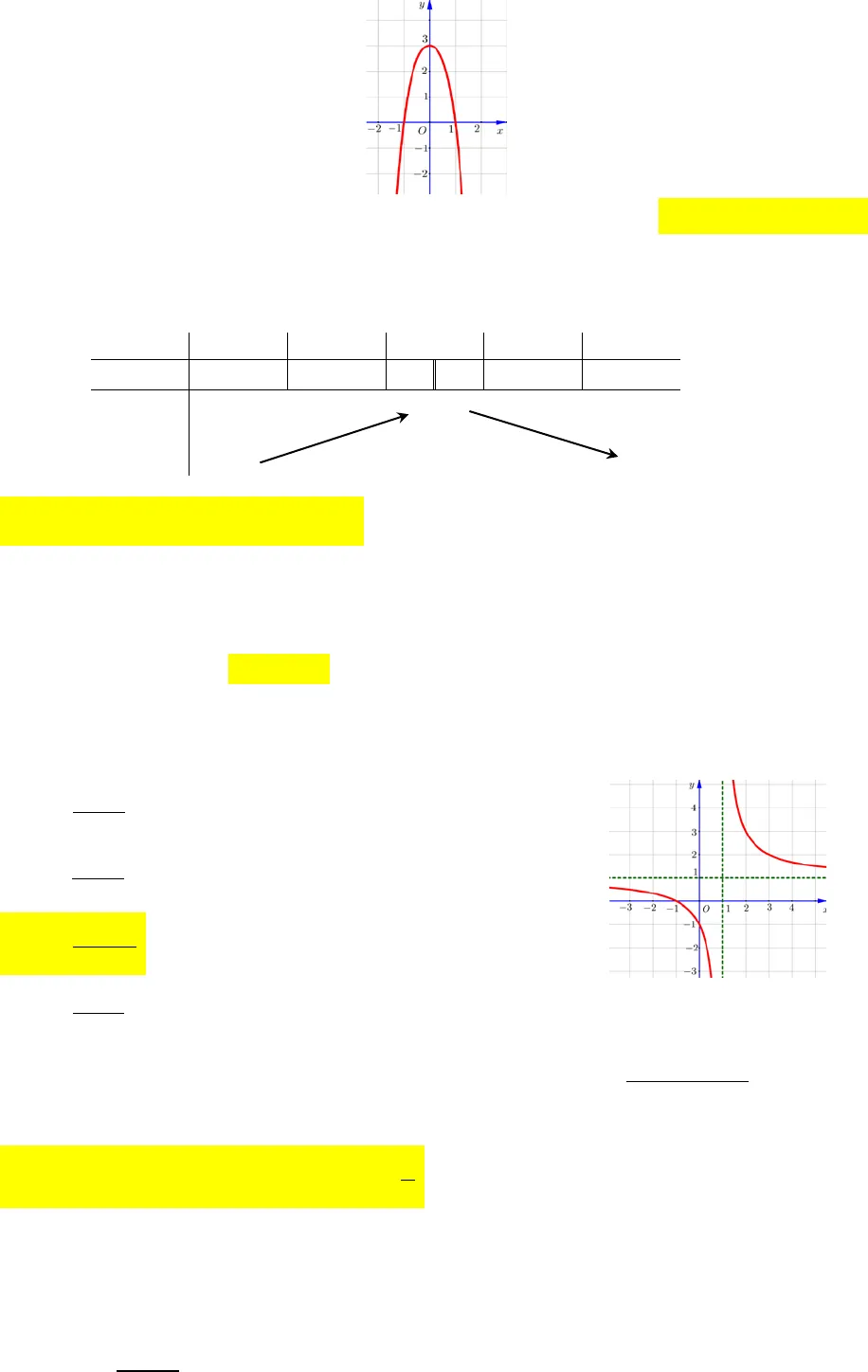A. 223yx x B.3233yx x  C.4223yx x  D.4223yxx  Câu 18. (THPT Chuyên Amsterdam – Hà Nội – 2017) Cho hàm số ()y fxcó bảng biến thiên trên khoảng 0; 2như sau. Khẳng định nào sau đây là đúng?A. Trên  0; 2, hàm số không có cực trị. B. Hàm số đạt cực đại tại1.x C. Hàm số đạt cực tiểu tại 1.x  D. Giá trị nhỏ nhất của hàm số là (0).fCâu 19. (THPT Chuyên Amsterdam – Hà Nội – 2017) Viết phương trình tiếp tuyến của đồ thị hàm số 4265yx x  tại điểm cực tiểu của nó?A. 5y  B.5y  C.0y  D.5yxCâu 20. (PTDTNT THCS&THPT An Lão – năm 2017) Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó làhàm số nào? A.11xyx.B.11xyx.C. 2122xyx.D.1xyx.Câu 21. (PTDTNT THCS&THPT An Lão – năm 2017) Cho hàm số 222 3223xxyxx. Khẳng địnhnào sau đây là khẳng định sai ? A. Đồ thị hàm số có tiệm cận ngang là 12y .B. Đồ thị hàm số có tiệm cận ngang là 2y .C. Đồ thị hàm số có ba đường tiệm cận. D. Đồ thị hàm số có hai tiệm cận đứng là 1x và3.x Câu 22. (PTDTNT THCS&THPT An Lão – năm 2017) Kết luận nào sau đây về tính đơn điệu của hàm số211xyxlà đúng?x−∞1+∞y′y( )1f( )0f( )2f