Download.vn Học tập Tài liệu Giáo viên
Bạn đang đọc: 28 Đề thi khảo sát giáo viên môn Toán THCS
28 Đề thi khảo sát giáo viên môn Toán THCS Đề kiểm tra khảo chất lượng giáo viên THCS môn Toán
Giới thiệu Tải về Bình luận
- 5
Mua tài khoản Download Pro để trải nghiệm website Download.vn KHÔNG quảng cáo & tải File cực nhanh chỉ từ 79.000đ. Tìm hiểu thêm Mua ngay
Có thể nói không chỉ có học sinh mới phải làm bài kiểm tra chất lượng mà giáo viên cũng sẽ phải thực hiện bài kiểm tra chất lượng. Chính vì vậy hôm nay chúng tôi xin mời quý thầy cô cùng tham khảo 28 Đề thi khảo sát giáo viên môn Toán THCS.
Đây là tài liệu vô cùng hữu ích giúp cho tất cả các thầy cô có thêm tài liệu ôn thi khảo sát chất lượng cấp THCS, tài liệu này sẽ bao gồ 28 đề tham khảo cùng với hướng dẫn cách làm, đã được chúng tôi sưu tầm và đăng tải tại đây. Sau đây chúng tôi xin mời các bạn cùng tham khảo nội dung của tài liệu này.
Đề kiểm tra khảo chất lượng giáo viên THCS môn Toán
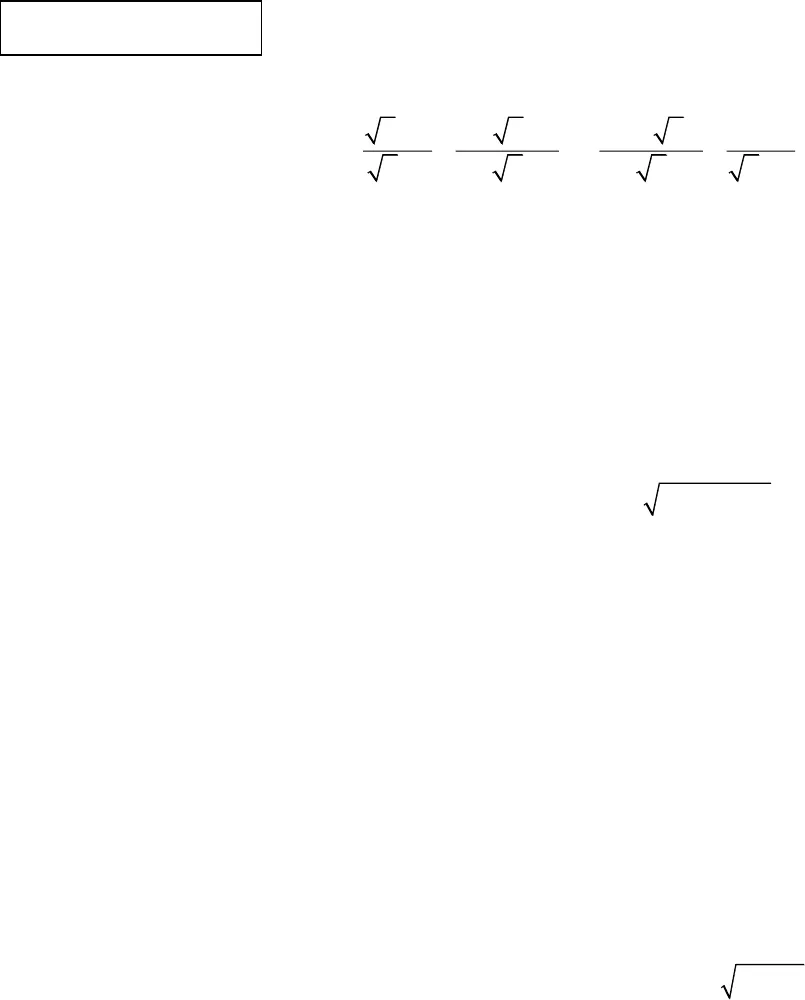 128 ĐỀ KHẢO SÁT GIÁO VIÊN MÔN TOÁN CÓ ĐÁP ÁN(8 đề minh họa)SỞ GD&ĐT VĨNH PHÚC KIỂM TRA CHẤT LƯỢNG CHUYÊN MÔN GIÁO VIÊN NĂM HỌC 2016 – 2017 MÔN: TOÁN – CẤP THCSThời gian làm bài: 180 phút, không kể thời gian giao đề Câu 1 (3,0 điểm). Cho biểu thức 2 3 2:1 2 2 2x x x x xPx x x x x x a) Rút gọn biểu thức P. b) Chứng minh1P.c) Tìm giá trị lớn nhất của P. Câu 2 (2,0 điểm). a) Cho hệ phương trình 3 2 112 3 2x y mx y m , trong đó x và y là ẩn, m là tham số. Tìm tất cả các giá trị của m để hệ phương trình (1) có nghiệm ;xysao cho22S x yb) Tìm các số thực x, y thỏa mãn22( 1) 2 2 2 3 3 0.x xy y y x y Câu 3 (1,0 điểm). Hai tổ cùng làm một công việc trong 15 giờ thì xong. Nếu tổ I làm trong 3 giờ và tổ II làm trong 5giờ thì họ làm được 25% công việc. Hỏi mỗi tổ làm riêng công việc đó trong bao lâu thì xong? Biết rằng năng suất mỗi tổ không thay đổi trong quá trình làm việc. Câu 4 (3,0 điểm). Cho đường tròn ;ORvà dây cung cố định AB . Gọi K là điểm chính giữa của cung nhỏ AB; N là điểm tùy ý trên đoạn thẳng AB (N khác A, B). Nối KN và kéo dài cắt ;ORtại điểm thứ hai là M. Chứng minh rằng a) Tam giác AKN và tam giác MKA đồng dạng. b) Đường thẳng AK tiếp xúc với đường tròn ngoại tiếp tam giác AMN.c) Tổng bán kính 2 đường tròn ngoại tiếp tam giác AMN và tam giác BMN không phụ thuộc vào vị trí điểm N. Câu 5 (1,0 điểm). Cho dãy số nađược xác định bởi 2111, 2 3 2 ,n n na a a a với n là số nguyêndương. Chứng minh rằng mọi số hạng của dãy số nađều là số nguyên.—————Hết —————Thí sinh không được sử dụng tài liệu. Cán bộ coi thi không giải thích gì thêm Họ và tên thí sinh:………………………………………………………… Số báo danh: .………………….. ĐỀ CHÍNH THỨC đạt giá trị nhỏnhất.
128 ĐỀ KHẢO SÁT GIÁO VIÊN MÔN TOÁN CÓ ĐÁP ÁN(8 đề minh họa)SỞ GD&ĐT VĨNH PHÚC KIỂM TRA CHẤT LƯỢNG CHUYÊN MÔN GIÁO VIÊN NĂM HỌC 2016 – 2017 MÔN: TOÁN – CẤP THCSThời gian làm bài: 180 phút, không kể thời gian giao đề Câu 1 (3,0 điểm). Cho biểu thức 2 3 2:1 2 2 2x x x x xPx x x x x x a) Rút gọn biểu thức P. b) Chứng minh1P.c) Tìm giá trị lớn nhất của P. Câu 2 (2,0 điểm). a) Cho hệ phương trình 3 2 112 3 2x y mx y m , trong đó x và y là ẩn, m là tham số. Tìm tất cả các giá trị của m để hệ phương trình (1) có nghiệm ;xysao cho22S x yb) Tìm các số thực x, y thỏa mãn22( 1) 2 2 2 3 3 0.x xy y y x y Câu 3 (1,0 điểm). Hai tổ cùng làm một công việc trong 15 giờ thì xong. Nếu tổ I làm trong 3 giờ và tổ II làm trong 5giờ thì họ làm được 25% công việc. Hỏi mỗi tổ làm riêng công việc đó trong bao lâu thì xong? Biết rằng năng suất mỗi tổ không thay đổi trong quá trình làm việc. Câu 4 (3,0 điểm). Cho đường tròn ;ORvà dây cung cố định AB . Gọi K là điểm chính giữa của cung nhỏ AB; N là điểm tùy ý trên đoạn thẳng AB (N khác A, B). Nối KN và kéo dài cắt ;ORtại điểm thứ hai là M. Chứng minh rằng a) Tam giác AKN và tam giác MKA đồng dạng. b) Đường thẳng AK tiếp xúc với đường tròn ngoại tiếp tam giác AMN.c) Tổng bán kính 2 đường tròn ngoại tiếp tam giác AMN và tam giác BMN không phụ thuộc vào vị trí điểm N. Câu 5 (1,0 điểm). Cho dãy số nađược xác định bởi 2111, 2 3 2 ,n n na a a a với n là số nguyêndương. Chứng minh rằng mọi số hạng của dãy số nađều là số nguyên.—————Hết —————Thí sinh không được sử dụng tài liệu. Cán bộ coi thi không giải thích gì thêm Họ và tên thí sinh:………………………………………………………… Số báo danh: .………………….. ĐỀ CHÍNH THỨC đạt giá trị nhỏnhất. 2SỞ GD&ĐT VĨNH PHÚC KIỂM TRA CHẤT LƯỢNG CHUYÊN MÔN GIÁO VIÊN NĂM HỌC 2016 -2017 HƯỚNG DẪN CHẤM MÔN TOÁN – CẤP THCS Câu 1 (3,0 điểm). Cho biểu thức 2 3 2:1 2 2 2x x x x xPx x x x x x a) Rút gọn biểu thức P. b) Chứng minh1P.c) Tìm giá trị lớn nhất của P. Nội dungĐiểm 04xx0,252 3 2:1 ( 1)( 2) ( 1)( 2) 2x x x x xPx x x x x x 0,254 3 2 2:( 1)( 2) ( 1)( 2)x x x x x xx x x x 0,2512xxx. Vậy 12xPxx0,25b)1,00Với 04xxta xét13-1= 122xxPx x x x 0,50Do0 3 0 xxmà32 0 02 xxxxx1 0 1 PP0,50c) 1,00TH 1: Nếu0 1 0 1 1 1 0x x x mà+ 2 0 0 (1)x x P 0,25TH 2:14xx1 2 1 1 4 4 41 1 1 31 1 1 1x x x xxxPx x x x 0,25Do1 à 4x v xnên10xvà401x.Áp dụng BĐT Côsi cho 2 số dương ta được: 4 1 11 3 2 4 3 7 (2)71xPPx Từ (1) và (2) ta suy ra17P 0,25Dấu”=” xảy ra41 1 2 91 x x xx. Vậy max197Px .0,25a) 1,00Điều kiện:
2SỞ GD&ĐT VĨNH PHÚC KIỂM TRA CHẤT LƯỢNG CHUYÊN MÔN GIÁO VIÊN NĂM HỌC 2016 -2017 HƯỚNG DẪN CHẤM MÔN TOÁN – CẤP THCS Câu 1 (3,0 điểm). Cho biểu thức 2 3 2:1 2 2 2x x x x xPx x x x x x a) Rút gọn biểu thức P. b) Chứng minh1P.c) Tìm giá trị lớn nhất của P. Nội dungĐiểm 04xx0,252 3 2:1 ( 1)( 2) ( 1)( 2) 2x x x x xPx x x x x x 0,254 3 2 2:( 1)( 2) ( 1)( 2)x x x x x xx x x x 0,2512xxx. Vậy 12xPxx0,25b)1,00Với 04xxta xét13-1= 122xxPx x x x 0,50Do0 3 0 xxmà32 0 02 xxxxx1 0 1 PP0,50c) 1,00TH 1: Nếu0 1 0 1 1 1 0x x x mà+ 2 0 0 (1)x x P 0,25TH 2:14xx1 2 1 1 4 4 41 1 1 31 1 1 1x x x xxxPx x x x 0,25Do1 à 4x v xnên10xvà401x.Áp dụng BĐT Côsi cho 2 số dương ta được: 4 1 11 3 2 4 3 7 (2)71xPPx Từ (1) và (2) ta suy ra17P 0,25Dấu”=” xảy ra41 1 2 91 x x xx. Vậy max197Px .0,25a) 1,00Điều kiện:  3Câu 2 (2,0 điểm).a) Cho hệ phương trình 3 2 112 3 2x y mx y m , trong đó x và y là ẩn, m là tham số. Tìm tất cả các giá trị của m để hệ phương trình (1) có nghiệm ;xysao cho22S x yđạt giá trị nhỏnhất.b) Tìm các số thực x, y thỏa mãn22( 1) 2 2 2 3 3 0x xy y y x y .Nội dungĐiểm a)1,00 3 2 13 2 12 3 2 1 3 22 3 2y x mx y mx x m mx y m 0,251xmym0,25Thay1xmymvào biểu thức 22 2 2 21 2 2 1S x y m m m m 0,25221 1 12 2 1 22 2 2S m m m Vậy min1122SmxyPT222 1 2 2 2 3 3 0 x x xy y y x y0,2522( ) 2( ).1 1 2 3 3 0( 1) 2 3 3 0.x y x y x yx y x y 0,25Do2( 1) 02 3 3 0xyxy 102 3 3 0xyxy 0,2501xyNội dungĐiểm Gọi thời gian tổ I làm một mình xong công việc là x (giờ,15x )Gọi thời gian tổ II làm một mình xong công việc là y (giờ,15y )Khi đó Năng suất của tổ I là 1x(công việc) Năng suất của tổ II là1y(công việc)Năng suất của cả 2 tổ là115(công việc)0,25b)1,00Điều kiện: 2 3 3 0(*)0,25 Nghiệm của phương trình là (0;1).0,25 Câu 3 (1,0 điểm). Hai tổ cùng làm một công việc trong 15 giờ thì xong. Nếu tổ I làm trong 3 giờ và tổ II làm trong 5 giờ thì họ làm được 25% công việc. Hỏi mỗi tổ làm riêng công việc đó trong bao lâu thì xong? Biết rằng năng suất mỗi tổ không thay đổi trong quá trình làm việc.
3Câu 2 (2,0 điểm).a) Cho hệ phương trình 3 2 112 3 2x y mx y m , trong đó x và y là ẩn, m là tham số. Tìm tất cả các giá trị của m để hệ phương trình (1) có nghiệm ;xysao cho22S x yđạt giá trị nhỏnhất.b) Tìm các số thực x, y thỏa mãn22( 1) 2 2 2 3 3 0x xy y y x y .Nội dungĐiểm a)1,00 3 2 13 2 12 3 2 1 3 22 3 2y x mx y mx x m mx y m 0,251xmym0,25Thay1xmymvào biểu thức 22 2 2 21 2 2 1S x y m m m m 0,25221 1 12 2 1 22 2 2S m m m Vậy min1122SmxyPT222 1 2 2 2 3 3 0 x x xy y y x y0,2522( ) 2( ).1 1 2 3 3 0( 1) 2 3 3 0.x y x y x yx y x y 0,25Do2( 1) 02 3 3 0xyxy 102 3 3 0xyxy 0,2501xyNội dungĐiểm Gọi thời gian tổ I làm một mình xong công việc là x (giờ,15x )Gọi thời gian tổ II làm một mình xong công việc là y (giờ,15y )Khi đó Năng suất của tổ I là 1x(công việc) Năng suất của tổ II là1y(công việc)Năng suất của cả 2 tổ là115(công việc)0,25b)1,00Điều kiện: 2 3 3 0(*)0,25 Nghiệm của phương trình là (0;1).0,25 Câu 3 (1,0 điểm). Hai tổ cùng làm một công việc trong 15 giờ thì xong. Nếu tổ I làm trong 3 giờ và tổ II làm trong 5 giờ thì họ làm được 25% công việc. Hỏi mỗi tổ làm riêng công việc đó trong bao lâu thì xong? Biết rằng năng suất mỗi tổ không thay đổi trong quá trình làm việc. 
