Đề thi tốt nghiệp THPT năm 2010 – môn Toán (Có hướng dẫn)

BỘ GIÁO DỤC VÀ ĐÀO TẠO Bạn đang đọc: Đề thi tốt nghiệp THPT năm 2010 – môn Toán (Có hướng dẫn) (Đề thi chính thức)

KỲ THI TỐT NGHIỆP TRUNG HỌC PHỔ THÔNG NĂM 2010 Môn thi: TOÁN − Giáo dục trung học phổ thông Thời gian làm bài: 150 phút, không kể thời gian giao đề

I. PHẦN CHUNG CHO TẤT CẢ THÍ SINH (7,0 điểm)

Câu 1 (3,0 điểm). Cho hàm số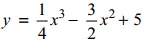

1) Khảo sát sự biến thiên và vẽ đồ thị của hàm số đã cho.

2) Tìm các giá trị của tham số m để phương trình x³ – 6x² + m = 0 có 3 nghiệm thực phân biệt.

Câu 2 (3,0 điểm).

1) Giải phương trình

2) Tính tích phân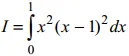

3) Cho hàm số 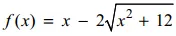. Giải bất phương trình f ‘(x) ≤ 0.

Câu 3 (1,0 điểm).
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với mặt phẳng đáy, góc giữa mặt phẳng (SBD) và mặt phẳng đáy bằng 60^o. Tính thể tích khối chóp S.ABCD theo a.

II. PHẦN RIÊNG – PHẦN TỰ CHỌN (3,0 điểm)

Thí sinh chỉ được làm một trong hai phần (phần 1 hoặc phần 2).

1. Theo chương trình Chuẩn

Câu 4.a (2,0 điểm). Trong không gian với hệ toạ độ Oxyz, cho 3 điểm A(1; 0; 0), B(0; 2; 0) và C(0; 0; 3).

1) Viết phương trình mặt phẳng đi qua A và vuông góc với đường thẳng BC.

2) Tìm toạ độ tâm mặt cầu ngoại tiếp tứ diện OABC.

Câu 5.a (1,0 điểm). Cho hai số phức z₁ = 1 + 2i và z₂ = 2 – 3i. Xác định phần thực và phần ảo của số phức z₁ – 2z₂

2. Theo chương trình Nâng cao

Câu 4.b (2,0 điểm). Trong không gian với hệ toạ độ Oxyz, cho đường thẳng Δ có phương trình: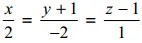

1) Tính khoảng cách từ điểm O đến đường thẳng Δ.

2) Viết phương trình mặt phẳng chứa điểm O và đường thẳng Δ.

Câu 5.b (1,0 điểm). Cho hai số phức và Xác định phần thực và phần ảo của số phức z₁ = 2 + 5i và z₂ = 3 – 4i. Xác định phần thực và phần ảo của số phức z₁.z₂

Download tài liệu để xem thêm chi tiết