Giải bài tập SGK Toán 8 Tập 1 trang 31, 32 giúp các em học sinh lớp 8 xem gợi ý giải các bài tập của Bài 12: Chia đa thức một biến đã sắp xếp. Thông qua đó, các em sẽ biết cách giải toàn bộ các bài tập của bài 12 Chương 1 phần Đại số trong sách giáo khoa Toán 8 Tập 1.
Bạn đang đọc: Giải Toán 8 Bài 12: Chia đa thức một biến đã sắp xếp
Giải bài tập Toán 8 tập 1 Bài 12 Chương I: Chia đa thức một biến đã sắp xếp
Lý thuyết bài 12: Chia đa thức một biến đã sắp xếp
Ta trình bày phép chia tương tự như cách chia các số tự nhiên. Với hai đa thức A và B của một biến, B ≠ 0 tồn tại duy nhất hai đa thức Q và R sao cho:
A = B . Q + R, với R = 0 hoặc bậc bé hơn bậc của 1
- Nếu R = 0, ta được phép chia hết.
- Nếu R ≠ 0, ta được phép chia có dư.
Giải bài tập Toán 8 trang 31 tập 1
Bài 67 (trang 31 SGK Toán 8 Tập 1)
Sắp xếp các đa thức theo lũy thừa giảm dần của biến rồi làm phép chia:
a) (x3 – 7x + 3 – x2) : (x – 3);
b) (2x4 – 3x2 – 3x2 – 2 + 6x) : (x2 – 2).
Gợi ý đáp án:
a) x3 – 7x + 3 – x2 = x3 – x2 – 7x + 3
Thực hiện phép chia:
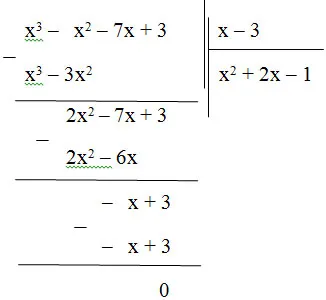
Vậy (x3 – x2 – 7x + 3) : (x – 3) = x2 + 2x – 1
b) 2x4 – 3x3 – 3x2 – 2 + 6x = 2x4 – 3x3 – 3x2 + 6x – 2
Thực hiện phép chia:
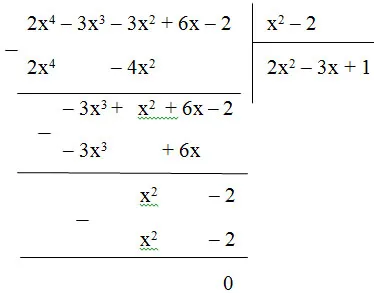
Vậy (2x4 – 3x3 – 3x2 + 6x – 2) : (x2 – 2) = 2x2 – 3x + 1.
Bài 68 (trang 31 SGK Toán 8 Tập 1)
Áp dụng hằng đẳng thức đáng nhớ để thực hiện phép chia:
a) (x2 + 2xy + y2) : (x + y);
c) (x2 – 2xy + y2) : (y – x).
b) (125x3 + 1) : (5x + 1);
Gợi ý đáp án:
a) (x2 + 2xy + y2) : (x + y) = (x + y)2 : (x + y) = x + y.
b) (125x3 + 1) : (5x + 1) = [(5x)3 + 1] : (5x + 1)
= (5x)2 – 5x + 1 = 25x2 – 5x + 1.
c) (x2 – 2xy + y2) : (y – x) = (x – y)2 : [-(x – y)] = – (x – y) = y – x
Hoặc (x2 – 2xy + y2) : (y – x) = (y2 – 2xy + x2) : (y – x)
= (y – x)2 : (y – x) = y – x.
Bài 69 (trang 31 SGK Toán 8 Tập 1)
Cho hai đa thức: A = 3x4 + x3 + 6x – 5 và B = x2 + 1. Tìm dư R trong phép chia A cho B rồi viết A dưới dạng A = B.Q + R
Gợi ý đáp án:
Thực hiện phép chia ta có:
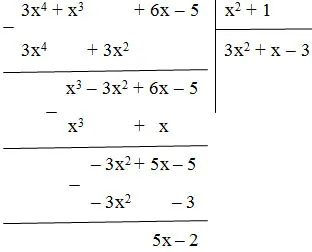
Vậy 3x4 + x3 + 6x – 5 = (x2 + 1).(3x2 + x – 3) + 5x – 2.
Giải bài tập Toán 8 trang 32 tập 1: Luyện tập
Bài 70 (trang 32 SGK Toán 8 Tập 1)
Làm tính chia:
a) (25x5 – 5x4 + 10x2) : 5x2 ;
b) (15x3y2– 6x2y – 3x2y2) : 6x2y
Gợi ý đáp án:
a) (25x5 – 5x4 + 10x2) : 5x2 = (25x5 : 5x2 ) – (5x4 : 5x2 ) + (10x2 : 5x2) = 5×3 – x2 + 2
b) (15x3y2 – 6x2y – 3x2y2) : 6x2y
= (15x3y2 : 6x2y) + (– 6x2y : 6x2y) + (– 3x2y2 : 6x2y)
= xy – 1 –
y =
xy –
y – 1.
Bài 71 (trang 32 SGK Toán 8 Tập 1)
Không thực hiện phép chia, hãy xét xem đa thức A có chia hết cho đa thức B hay không.
a) A = 15x4 – 8x3 + x2
B = x2
b) A = x2 – 2x + 1
B = 1 – x
Gợi ý đáp án:
a) Ta có 15x4 ; 8x3 ; x2 chia hết cho 1/2x2 nên đa thức A chia hết cho B.
b) A chia hết cho B, vì x2 – 2x + 1 = (1 – x)2, chia hết cho 1 – x
Bài 72 (trang 32 SGK Toán 8 Tập 1)
Làm tính chia:
(2x4 + x3 – 3x2 + 5x – 2) : (x2 – x + 1).
Gợi ý đáp án:
Thực hiện phép chia:
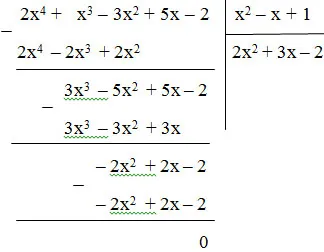
Vậy (2x4 + x3 – 3x2 + 5x – 2) : (x2 – x + 1) = 2x2 + 3x – 2
Bài 73 (trang 32 SGK Toán 8 Tập 1)
Tính nhanh:
a) (4x2 – 9y2) : (2x – 3y) ;
c) (8x3 + 1) : (4x2 – 2x + 1) ;
b) (27x3 – 1) : (3x – 1)
d) (x2 – 3x + xy – 3y) : (x + y)
Gợi ý đáp án:
a) (4x2 – 9y2) : (2x – 3y)
(Sử dụng HĐT để phân tích số bị chia thành tích)
= [(2x)2 – (3y)2] : (2x – 3y)
(Xuất hiện hằng đẳng thức (3))
= (2x – 3y)(2x + 3y) : (2x – 3y)
= 2x + 3y.
b) (27x3 – 1) : (3x – 1)
(Sử dụng HĐT để phân tích số bị chia thành tích)
= [(3x)3 – 1] : (3x – 1)
(Xuất hiện hằng đẳng thức (7))
= (3x – 1).[(3x)2 + 3x.1 + 12] : (3x – 1)
= (3x – 1).(9x2 + 3x + 1) : (3x – 1)
= 9x2 + 3x + 1
c) (8x3 + 1) : (4x2 – 2x + 1)
(Sử dụng HĐT để phân tích số bị chia thành tích)
= [(2x)3 + 1] : (4x2 – 2x + 1)
(Xuất hiện HĐT (6))
= (2x + 1).[(2x)2 – 2x.1 + 12] : (4x2 – 2x + 1)
= (2x + 1).(4x2 – 2x + 1) : (4x2 – 2x + 1)
= 2x + 1.
d) (x2 – 3x + xy – 3y) : (x + y)
(Nhóm hạng tử để phân tích số bị chia thành tích)
= [(x2 – 3x) + (xy – 3y)] : (x + y)
= [x.(x – 3) + y.(x – 3)] : (x + y)
= (x + y).(x – 3) : (x + y)
= x – 3.
Bài 74 (trang 32 SGK Toán 8 Tập 1)
Tìm số a để đa thức 2x3 – 3x2 + x + a chia hết cho đa thức x + 2.
Gợi ý đáp án:
Cách 1: Thực hiện phép chia:
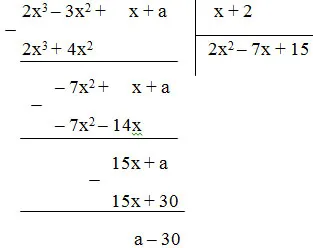
2x3 – 3x2 + x + a chia hết cho x + 2
⇔ số dư = a – 30 = 0
⇔ a = 30.
Cách 2: Phân tích 2x3 – 3x2 + x + a thành nhân tử có chứa x + 2.
2x3 – 3x2 + x + a
= 2x3 + 4x2 – 7x2 – 14x + 15x + 30 + a – 30
(Tách -3x2 = 4x2 – 7x2; x = -14x + 15x)
= 2x2(x + 2) – 7x(x + 2) + 15(x + 2) + a – 30
= (2x2 – 7x + 15)(x + 2) + a – 30
2x3 – 3x2 + x + a chia hết cho x + 2 ⇔ a – 30 = 0 ⇔ a = 30.

