Đề thi tuyển sinh lớp 10 THPT Chuyên tỉnh Đồng Tháp – Môn Toán (năm học 2012 – 2013)

Câu 1: (2,0 điểm)

a. Tính giá trị của biểu thức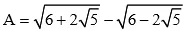

b. Với giá trị nào của x thì biểu thức sau có nghĩa: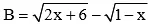

c. Chứng minh bất đẳng thức sau:

Câu 2: (2,0 điểm)

Cho hệ phương trình:

a. Giải hệ phương trình (I) khi a = 3.

b. Tìm a để hệ phương trình (I) có nghiệm duy nhất.

c. Với giá trị nào của a thì hệ phương trình (I) có nghiệm nguyên. Tìm nghiệm nguyên đó.

Câu 3: (1,5 điểm)

Cho hai hàm số y = (m + 1)x + 4 – m và y = x²

a. Xác định m để đồ thị hai hàm số cắt nhau tại điểm có hoành độ bằng -3 .

b. Vẽ đồ thị hai hàm số đã cho trên cùng một mặt phẳng tọa độ với giá trị m tìm được ở câu a.

Câu 4: (1,5 điểm)

Cho phương trình x² – 6x + 1 = 0 (1). Gọi x₁, x₂ là hai nghiệm của phương trình (1), đặt

a. Tính S₁; S₂; S₃

b. Chứng minh rằng: S_n+2 = 6S_n+1 – S_n

Câu 5: (3,0 điểm)

a. Tìm độ dài hai cạnh góc vuông của tam giác ABC vuông tại A, biết đường cao AH = 12/5 cm; BC = 5cm.

b. Cho đường tròn (O). Từ một điểm M nằm bên ngoài đường tròn vẽ tiếp tuyến MA (A là tiếp điểm). Tia MO cắt (O) tại B và C (B nằm giữa M và O); kẻ AH vuông góc BC (H thuộc BC) , tia AH cắt (O) tại D (D # A).
– Chứng tỏ AMDO là tứ giác nội tiếp.
– Chứng minh BM.CH = BH.CM

Download tài liệu để xem thêm chi tiết