|
SỞ GIÁO DỤC VÀ ĐÀO TẠO Bạn đang đọc: Đề thi học sinh giỏi lớp 12 THPT tỉnh Bắc Ninh môn Toán (năm học 2010 – 2011) ĐỀ CHÍNH THỨC |
KỲ THI CHỌN HỌC SINH GIỎI CẤP TỈNH LỚP 12 THPT ĐỀ THI MÔN: TOÁN |
Câu 1: (5 điểm)
1/ Cho hàm số y = x3 – 3x + 2 = 0 có đồ thị là (T). Giả sử A, B, C là ba điểm thẳng hàng trên (T), tiếp tuyến của (T) tại các điểm A, B, C lần lượt cắt (T) tại các điểm A’, B’, C’ (tương ứng khác A, B, C). Chứng minh rằng A’, B’, C’ thẳng hàng.
2/ Cho hàm số , chứng minh rằng y = x2n+1 + 2011x + 2012 (1) với mọi số nguyên dương n đồ thị hàm số (1) luôn cắt trục hoành tại đúng một điểm.
Câu 2: (5 điểm)
1/ Giải phương trình: 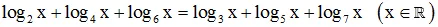
2/ Giải phương trình: 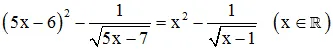
Câu 3: (3 điểm)
Kí hiệu Cknlà tổ hợp chập k của n phần tử 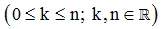 , tính tổng sau:
, tính tổng sau: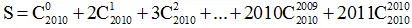
Câu 4: (5 điểm)
1/ Cho hình chóp tứ giác S.ABCD, có đáy ABCD là hình bình hành, AD = 4a (a > 0), các cạnh bên của hình chóp bằng nhau và bằng 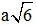 . Tìm cosin của góc giữa hai mặt phẳng (SBC) và (SCD) khi thể tích của khối chóp S.ABCD là lớn nhất.
. Tìm cosin của góc giữa hai mặt phẳng (SBC) và (SCD) khi thể tích của khối chóp S.ABCD là lớn nhất.
2/ Cho tứ diện ABCD có góc BAC = 600, CAD = 1200. Gọi E là chân đường phân giác trong góc A của tam giác ABD. Chứng minh rằng tam giác ACE vuông.
Câu 5: (2 điểm)
Cho hai số thực x, y thỏa mãn: 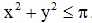 . Chứng minh rằng:
. Chứng minh rằng: 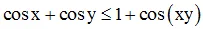
Download tài liệu để xem thêm chi tiết

