Giải Toán lớp 7 trang 87 tập 1 Cánh diều giúp các bạn học sinh có thêm nhiều gợi ý tham khảo để trả lời câu hỏi trong SGK Bài tập cuối chương 3 Hình học trực quan.
Bạn đang đọc: Toán 7 Bài tập cuối chương III – Cánh diều
Bài tập cuối chương 3 Toán 7 Cánh diều trang 87 được biên soạn với các lời giải chi tiết, đầy đủ và chính xác bám sát chương trình sách giáo khoa môn Toán lớp 7. Giải Bài tập cuối chương 3 lớp 7 là tài liệu cực kì hữu ích hỗ trợ các em học sinh trong quá trình giải bài tập. Đồng thời phụ huynh có thể sử dụng để hướng dẫn con em học tập và đổi mới phương pháp giải phù hợp hơn.
Giải Toán 7 Bài tập cuối chương III – Cánh diều
Đáp số Toán 7 trang 87 sách Cánh diều
Bài 1
|
Hình hộp chữ nhật |
Hình lập phương |
|
|
Các mặt bên đều là hình vuông |
S |
Đ |
|
Các mặt bên bằng nhau |
S |
Đ |
|
Các cạnh bằng nhau |
S |
Đ |
Bài 2
a) 150 (cm2)
b) 1352 (cm2).
Bài 3
a) V = 33 =27 (cm3)
b) 8 (lần)
Bài 4
V = 120 lít
Bài 5
V = 369 (m3).
Hướng dẫn giải bài tập cuối chương III Toán 7 – Tập 1
Bài 1
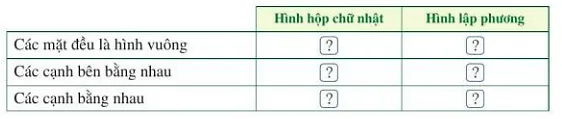
Chọn từ “đúng (Đ)”, “sai (S)” thích hợp cho ?? trong bảng sau:
Cách giải
Đặc điểm của hình hộp chữ nhật, hình lập phương
Gợi ý đáp án
|
Hình hộp chữ nhật |
Hình lập phương |
|
|
Các mặt bên đều là hình vuông |
S |
Đ |
|
Các mặt bên bằng nhau |
S |
Đ |
|
Các cạnh bằng nhau |
S |
Đ |
Bài 2
a) Cho một hình lăng trụ đứng có độ dài cạnh bên là 10 cm và đáy là tam giác. Biết tam giác đó có độ dài các cạnh lần lượt là 4 cm, 5 cm, 6 cm. Tính diện tích xung quanh của hình lăng trụ đứng đã cho.
b) Cho một hình lăng trụ đứng có độ dài cạnh bên là 20 cm và đáy là một hình thang cân. Biết hình thang cân đó có độ dài cạnh bên là 13 cm, độ dài hai đáy lần lượt là 8 cm, 18 cm và chiều cao là 12 cm. Tính diện tích toàn phần (tức là tổng diện tích các mặt) của hình lăng trụ đứng đã cho.
Cách giải
Diện tích xung quanh hình lăng trụ đứng: Sxq = Chu vi đáy. chiều cao
Diện tích toàn phần = diện tích xung quanh + diện tích 2 đáy
Gợi ý đáp án
a) Chu vi đáy của hình lăng trụ đứng tam giác là: 4 + 5 + 6 =15 (cm)
Diện tích xung quanh hình lăng trụ đứng tam giác là: Sxq = 15.10 = 150 (cm2)
b) Chu vi đáy của hình lăng trụ đứng tứ giác là: 13 + 13 + 8 + 18 = 52 (cm)
Diện tích xung quanh của hình lăng trụ đứng đó là: Sxq = 52.20 = 1040 (cm2)
Diện tích một đáy hình lăng trụ đứng đó là:
S= 1/ 2 ( 8 + 18 ) .12 = 1 /2 .26.12 =156 (cm2).
Diện tích toàn phần hình lăng trụ đứng đó là:
Stp = 156.2 + 1040 = 1352 (cm2).
Bài 3
a) Một hình lập phương có độ dài cạnh là 3 cm. Tính thể tích của hình lập phương đó.
b) Một hình lập phương mới có độ dài cạnh gấp đôi độ dài cạnh của hình lập phương ban đầu. Tính thể tích của hình lập phương mới và cho biết thể tích của hình lập phương mới gấp bao nhiêu lần thể tích của hình lập phương ban đầu.
Gợi ý đáp án
a) Thể tích hình lập phương đó là:
V = 33 =27 (cm3)
b) Cạnh của hình lập phương mới là: 2. 3 = 6 (cm)
Thể tích của hình lập phương mới là: V’ = 63 = 216 (cm3)
Thể tích hình lập phương mới gấp số lần thể tích của hình lập phương ban đầu là:
216 : 27=8 (lần)
Chú ý: Khi tăng độ dài cạnh hình lập phương lên a lần thì thể tích hình lập phương tăng lên a3 lần.
Bài 4
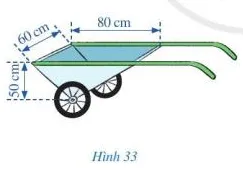
Hình 33 mô tả một xe chở hai bánh mà thùng chứ của nó có dạng lăng trụ đứng tam giác với các kích thước cho trên. Hỏi thùng chứa của xe chở hai bánh có kích thước là bao nhiêu?
Gợi ý đáp án
Ta biểu diễn thùng xe thành hình lăng trụ đứng tam giác như hình vẽ trên với hai đáy là ABC và DEF chiều cao của đáy là BH = 50 cm, độ dài cạnh bên là BE = 60 cm, cạnh đáy AC = 80 cm.
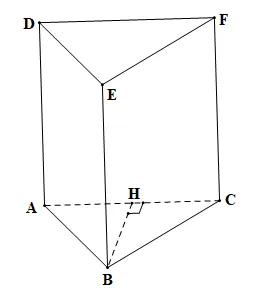
Thùng chứa là hình lăng trụ tam giác có cạnh bên là 60 cm, cạnh đáy là 80 cm, chiều cao ứng với đáy đó là 50 cm
Diện tích đáy của hình lăng trụ tam giác là: Sđáy = 50.80 : 2 = 2 000 (cm2)
Thùng chứa của xe chở hai bánh đó có thể tích bằng:
V = Sđáy . h = 2 000. 60 = 120 000 (cm3) = 120 lít
Bài 5
Một ngôi nhà có cấu trúc và kích thước như Hình 34. Tính thể tích phần không gian được giới hạn bởi ngôi nhà đó.
Hướng dẫn: Phần không gian của ngôi nhà đó có thể chia thành 2 phần: Phần không gian có dạng một hình hộp chữ nhật và phần không gian còn lại có dạng một hình lăng trụ đứng tam giác.
Gợi ý đáp án
Thể tích phần không gian của ngôi nhà có dạng hình hộp chữ nhật là:
V1 = 3,5.6.15 = 315 (m3)
Diện tích đáy phần không gian mái nhà có hình lăng trụ đứng là:
S = .1,2.6=3,6 (m2)
Thể tích phần không gian có hình lăng trụ đứng là:
V2 = 3,6 . 15 = 54 (m3)
Thể tích phần không gian được giới hạn bởi ngôi nhà đó là:
54 + 315 = 369 (m3).
Lý thuyết Hình học trực quan
I. Hình hộp chữ nhật
– Có 6 mặt, 12 cạnh, 8 đỉnh, 4 đường chéo.
– Các mặt đều là hình chữ nhật.
– Các cạnh bên bằng nhau.
II. Hình lập phương
– Có 6 mặt, 12 cạnh, 8 đỉnh, 4 đường chéo
– Các mặt đều là hình vuông
– Các cạnh đều bằng nhau
III. Hình lăng trụ đứng tam giác
– Hình lăng trụ đứng tam giác có 5 mặt, 9 cạnh, 6 đỉnh.
– Hai mặt đáy cùng là tam giác và nằm trong hai mặt phẳng song song với nhau; Mỗi mặt bên là hình chữ nhật;
– Các cạnh bên bằng nhau;
– Chiều cao của hình lăng trụ đứng tam giác là độ dài cạnh bên.

