Các bài Toán điển hình lớp 5 và phương pháp giảng dạy là tài liệu tham khảo hay dành cho quý thầy cô, quý phụ huynh và các em học sinh. Với tài liệu này các thầy cô giáo có thể hướng dẫn các em học sinh cách giải các dạng bài tập Toán lớp 5 khác nhau. Đồng thời giúp các em học sinh rèn luyện kỹ năng giải Toán với nhiều dạng bài tập, nhiều đề Toán khác nhau nhằm chuẩn bị cho các kỳ thi học sinh giỏi và kiểm tra trên lớp.
Bạn đang đọc: Các bài Toán điển hình lớp 5 và phương pháp giảng dạy
Toán điển hình lớp 5
1. Bài toán về tìm số trung bình cộng
a. Nội dung:
Bài toán về tìm số trung bình cộng đã được học ở lớp 4. Trong chương trình Toán 5 không có phần dành riêng cho toán trung bình cộng mà chỉ lồng ghép đan xen với các nội dung khác để ôn tập, củng cố, khắc sâu và mở rộng nhằm giúp học sinh rèn luyện kĩ năng giải loại toán này ở mức độ thành thạo hơn. Trong mỗi bài toán, nội dung cũng đan xen với các loại toán khác. Vì vậy, xét về mức độ liên quan thì dung lượng dành cho toán trung bình cộng ở Toán 5 là khoảng trên 10 bài.
b. Phương pháp giảng dạy:
Do dung lượng không nhiều, cũng không phân phối thành tiết dạy riêng biệt nên khi dạy, giáo viên cần chú ý nội dung tích hợp của các bài toán mà củng cố cho học sinh kịp thời, chính xác và đảm bảo mục tiêu bài dạy.
Khi dạy loại toán trung bình cộng này, để đạt kết quả cao hơn, giáo viên cần thực hiện theo 2 mức độ sau đây:
Mức độ 1: Củng cố về cách tìm số trung bình cộng
Ví dụ: Tìm số trung bình cộng của: 19 ; 34 và 46 (Toán 5 – trang 177).
Mục đích của bài toán này là giúp học sinh củng cố về cách tìm số trung bình cộng.
Vì vậy, khi dạy bài toán này, giáo viên cần yêu cầu học sinh nêu cách tìm số trung bình cộng của hai số, ba số, bốn số,…
Sau đó yêu cầu học sinh thực hành giải bài toán để nắm được cách giải:
Bài giải:
Trung bình cộng của 19 ; 34 và 46 là:
(19 + 34 + 46) : 3 = 33.
Đáp số: 33.
Mức độ 2: Giải bài toán có lời văn
Bài toán: Một người đi xe đạp trong 3 giờ, giờ thứ nhất đi được 12km, giờ thứ hai đi được 18km, giờ thứ ba đi được nửa quáng đường đi trong hai giờ đầu. Hỏi trung bình mỗi giờ người đó đi được bao nhiêu ki-lô-mét ? (Toán 5 – trang 170)
Bài toán này là dạng toán “Tìm số trung bình cộng”. Trước hết, yêu cầu học sinh tìm quãng đường xe đạp đi trong giờ thứ ba: (12 + 18) : 2 = 15 (km).
Từ đó tính được trung bình mỗi giờ xe đạp đi được quãng đường là:
(12 + 18 + 15) : 3 = 15 (km).
2. Bài toán về “Tìm hai số khi biết tổng và hiệu của hai số đó”
a. Nội dung:
Dạng toán “Tìm hai số khi biết tổng và hiệu của hai số đó” đã được học ở lớp 4. Vì vậy, trong chương trình Toán 5 gồm có 6 bài, không trình bày riêng mà chỉ phân bố rải đều trong chương trình và ở phần ôn tập cuối năm, mục đích là để củng cố kiến thức thường xuyên cho học sinh.
b. Phương pháp giảng dạy:
Khi dạy dạng toán này, giáo viên cần tập trung học sinh vào việc nhận dạng bài toán và nêu cách giải. Một trong những điểm cần lưu ý khi dạy bài toán này là việc tóm tắt bài toán bằng sơ đồ đoạn thẳng.
Việc hướng dẫn học sinh tóm tắt bài toán bằng sơ đồ đoạn thẳng là bước quan trọng nhất. Nếu tóm tắt đầy đủ và chính xác sẽ giúp cho các em dễ dàng nhận ra mối liên hệ giữa các yếu tố của bài toán đã cho. Từ đó, các em sẽ tìm ra được cách giải thuận lợi hơn.
Chẳng hạn: Một mảnh đất hình chữ nhật có chu vi 120m. Chiều dài hơn chiều rộng 10m. Tính diện tích mảnh đất đó.
Điều then chốt ở đây là học sinh phải hiểu được Tổng của chiều dài và chiều rộng chính là nửa chu vi; chiều dài chính là số lớn; chiều rộng chính là số bé. Khi nhận biết được điều này, học sinh sẽ dễ dàng tìm ra được chiều dài và chiều rộng. Khi đó, giáo viên cần lưu ý thêm là: Sau khi tìm được chiều dài, chiều rộng thì còn phải tính diện tích mảnh đất.
Tóm tắt:

Bài giải:
Chiều dài mảnh đất hình chữ nhật là:
(60 + 10) : 2 = 35 (m).
Chiều rộng mảnh đất hình chữ nhật là:
35 – 10 = 25 (m).
Diện tích mảnh đất hình chữ nhật là:
35 25 = 875 (m2).
Đáp số : 875 m2.
3. Bài toán về “Tìm hai số khi biết tổng và tỉ số của hai số đó”
a. Nội dung:
Dạng toán này cũng đã được học ở lớp 4. Trong chương trình Toán 5, dạng toán “Tìm hai số khi biết tổng và tỉ số của hai số đó” chỉ gồm có 5 bài và được phân bố rải đều và trong chương trình ôn tập cuối năm, mục đích là giúp học sinh củng cố và rèn luyện kỹ năng vận dụng. Từ đó, các em có thể tiếp cận và giải được các bài tập nâng cao nhằm mở rộng thên kiến thức.
b. Phương pháp giảng dạy:
Khi dạy dạng toán này, cũng tương tự như dạng toán 2, giáo viên cần tập trung học sinh vào việc nhận dạng bài toán và nêu cách giải. Một trong những điểm cần lưu ý khi dạy bài toán này là việc tóm tắt bài toán bằng sơ đồ đoạn thẳng.
Chẳng hạn: Lớp 5A có 35 học sinh. Số học sinh nam bằng số học sinh nữ. Hỏi số học sinh nữ hơn số học sinh nam là bao nhiêu em?
Điều quan trọng ở đây là học sinh phải nhận dạng và tóm tắt được bài toán bằng sơ đồ đoạn thẳng.Vì vậy trước khi dạy các bài toán thuộc loại toán này, giáo viên cần củng cố, khắc sâu cho học sinh về tỉ số (đã được học ở lớp 4). Sau đó, giáo viên cần lưu ý cho học sinh là: dựa theo sơ đồ đoạn thẳng để giải bài toán.
Tóm tắt:
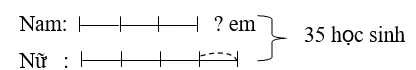
Bài giải:
Theo sơ đồ, tổng số phần bằng nhau là:
3 + 4 = 7 (phần).
Số học sinh nam của lớp 5A là:
35 : 7 3 = 15 (học sinh).
Số học sinh nữ của lớp 5A là:
35 – 15 = 20 (học sinh).
Số học sinh nữ nhiều hơn số học sinh nam là:
20 – 15 = 5 (học sinh).
Đáp số : 5 học sinh.
Ngoài ra, giáo viên có thể gợi ý để học sinh suy nghĩ và tìm cách giải khác.
Chẳng hạn:
Theo sơ đồ, số học sinh nữ nhiều hơn số học sinh nam số phần là:
4 – 3 = 1 (phần).
Số học sinh nữ nhiều hơn số học sinh nam là:
35 : 7 = 5 (học sinh).
Đáp số: 5 học sinh.
4. Bài toán về “Tìm hai số khi biết hiệu và tỉ số của hai số đó”
a. Nội dung:
Dạng toán này cũng đã được học ở lớp 4. Trong chương trình Toán 5 gồm có 4 bài được trình bày đan xen trong các bài, các chương và trong phần ôn tập cuối năm nhằm mục đích nhắc nhở các em các dạng toán đã học. Từ đó, các em có thể đầu tư để nâng cao, mở rộng kiến thức đã được học qua các lớp dưới.
b. Phương pháp giảng dạy:
Khi dạy dạng toán này, giáo viên cũng thực hiện các bước như dạng toán .Tức là cũng cần tập trung học sinh vào việc nhận dạng bài toán và nêu cách giải. Một trong những điểm cần lưu ý khi dạy bài toán này là việc tóm tắt bài toán bằng sơ đồ đoạn thẳng.
Chẳng hạn: Lan có ít hơn Hằng 15 bông hoa. Số hoa của Lan bằng số hoa của Hằng. Hỏi mỗi bạn có mấy bông hoa?
Điều quan trọng ở đây là học sinh phải nhận dạng và tóm tắt được bài toán bằng sơ đồ đoạn thẳng.Vì vậy trước khi dạy các bài toán thuộc loại toán này, giáo viên cần củng cố, khắc sâu cho học sinh về tỉ số (đã được học ở lớp 4). Sau đó, giáo viên cần lưu ý cho học sinh là: dựa theo sơ đồ để giải bài toán.
Tóm tắt:
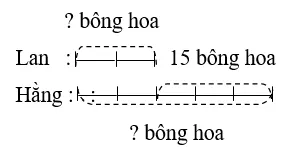
Bài giải:
Theo sơ đồ, hiệu số phần bằng nhau là:
5 – 2 = 3 (phần).
Số bông hoa của Lan là:
15 : 3 2 = 10 (bông hoa).
Số bông hoa của Hằng là:
10 + 15 = 25 (bông hoa).
Đáp số : 10 bông hoa ; 25 bông hoa.
5. Bài toán liên quan đến quan hệ tỉ lệ
5.1. Trường hợp đại lượng này tăng (hoặc giảm) bao nhiêu lần thì đại lượng kia cũng tăng hoặc giảm bấy nhiêu lần:
a. Nội dung:
Trong chương trình Toán 5, Dạng toán này là dạng toán mới. Dạng toán này gồm 20 bài toán được trình bày thành 2 bài dạy (tiết 16,17) và rải đều cho các tiết học sau đó và trong chương trình ôn tập cuối năm. Tiết 16 là tiết học giúp học sinh nhận dạng bài toán và trang bị cho học sinh 2 cách giải của dạng toán này. Tiết 17 là tiết luyện tập nhằm giúp học sinh rèn luyện kĩ năng thực hành. Các bài tập rải đều cho các bài học sau đó nhằm giúp các em rèn luyện kĩ năng, kĩ xảo cũng như mở rộng và nâng cao kiến thức.
b. Phương pháp giảng dạy:
Đây là dạng toán thường gặp và mang tính thực tế cao. Các em rất có hứng thú với dạng toán này. Vì vậy, khi dạy dạng toán này, giáo viên cần tập trung vào việc lấy ví dụ gần gũi, sát thực tế ở địa phương để học sinh vừa học tập vừa có thể vận dụng trong cuộc sống hằng ngày. Một trong những điểm cần lưu ý khi dạy bài toán này là việc tóm tắt bài toán sao cho ngắn gọn và đễ hiểu. Việc giải bài toán được thực hiện theo hai cách: cách “rút về đơn vị”, cách “tìm tỉ số”. Trong mỗi cách dạy cần thực hiện theo các bước cơ bản . Bước quan trong nhất là bước “rút về đơn vị” (hoặc “Tìm tỉ số”). Do vậy, khi dạy dạng toán này cần khắc sâu cho học sinh mỗi bước này trong mỗi cách giải của bài toán. Mặt khác, cũng cần lưu ý cho học sinh là: chỉ cần trình bày một trong hai cách giải của bài toán.
Ví dụ: Một ô-tô trong 2 giờ đi được 90km. Hỏi trong 4 giờ ô-tô đó đi được bao nhiêu ki-lô-mét ?
Khi dạy bài toán này, giáo viên cần hướng dẫn học sinh tóm tắt bài toán ngắn gọn, dễ hiểu. Tránh để học sinh ghi dài dòng, không cần thiết.
Tóm tắt:
2 giờ : 90 km
4giờ : ….km ?
Khi hướng dẫn học sinh giải cần nhấn mạnh cho học sinh mỗi bước quan trọng trong mỗi cách, đó là:
Bước 1 trong cách 1 là bước “rút về đơn vị”
Trong 1 giờ ô-tô đi được là :
90 : 2 = 45 (km).
Bước 1 trong cách 2 là bước “ tìm tỉ số”
4 giờ gấp 2 giờ số lần là :
4 : 2 = 2 (lần).
Khi nắm chắc được mỗi bược cơ bản trong mỗi cách giải bài toán, học sinh sẽ dễ dàng tìm ra kết quả của bài toán.
5.2. Trường hợp đại lượng này tăng (hoặc giảm) bao nhiêu lần thì đại lượng kia giảm hoặc tăng bấy nhiêu lần và ngược lại:
a. Nội dung:
Trong chương trình Toán 5, Dạng toán này là dạng toán mới. Dạng toán này gồm 10 bài toán được trình bày thành 2 bài dạy (tiết 18,19) và rải đều cho các tiết học sau đó và trong chương trình ôn tập cuối năm. Tiết 18 là tiết học giúp học sinh nhận dạng bài toán và trang bị cho học sinh 2 cách giải của dạng toán này. Tiết 19 là tiết luyện tập nhằm giúp học sinh rèn luyện kĩ năng thực hành. Các bài tập rải đều cho các bài học sau đó nhằm giúp các em rèn luyện kĩ năng, kĩ xảo cũng như mở rộng và nâng cao kiến thức.
b. Phương pháp giảng dạy:
Dạng toán này cũng thường gặp và mang tính thực tế cao như dạng toán 5.1. Vì vậy, khi dạy dạng toán này, giáo viên cũng cần thực hiện các bước như khi dạy dạng toán 5.1. Tuy nhiên vấn đề cần đặc biệt chú ý ở đây là sự xác định mối quan hệ giữa hai đại lượng. Vì vậy khi dạy loại toán này, giáo viên cần làm rõ mối quan hệ giữa hai đại lượng đã cho trong một bài toán. Đồng thời cần nêu thêm ví dụ gần gũi với học sinh để học sinh nắm bắt nhằm tránh nhầm lẫn với mối quan hệ giữa hai đại lượng trong các bài toán thuộc loại toán 5.1.
Ví dụ: Muốn đắp xong nền nhà trong 2 ngày, cần có 12 người. Hỏi muốn đắp xong nền nhà đó trong 4 ngày thì cần bao nhiêu người? (Mức làm của mỗi người như nhau).
Khi dạy bài toán này, giáo viên cần làm rõ mối quan hệ giữa số ngày và số người. Số người ở đây là số người làm trong mỗi ngày. Vì vậy cần phân tích cho học sinh thấy rõ muốn đắp xong nền nhà trong thời gian dài hơn thì cần giảm số người làm trong mỗi ngày. Đồng thời, giáo viên cần nêu thêm vài ví dụ khác để học sinh dễ nắm bắt.
Chẳng hạn: Muốn quét xong lớp học trong 6 phút thì cần 2 bạn. Hỏi muốn quét xong lớp học trong 3 phút thì cần mấy bạn? (Mức làm của mỗi bạn là như nhau).
Hoặc: Muốn hái xong một rẫy cà phê trong 10 ngày thì cần 6 người. Hỏi muốn hái xong rẫy cà phê trong 5 ngày thì cần bao nhiêu người? (Mức làm mỗi người như nhau).
Thông qua việc phân tích hai ví dụ gần gũi với các em hằng ngày, các em sẽ nắm vững mối quan hệ giữa hai đại lượng của bài toán dạng này (Khi đại lượng này tăng (hoặc giảm) bao nhiêu lần thì đại lượng kia giảm (hoặc tăng) bấy nhiêu lần). Khi học sinh đã nắm chắc mối quan hệ giữa hai đại lượng thì các em sẽ dễ dàng vận dụng phương pháp phù hợp để giải bài toán.
Xem chi tiết tại file Tải về.

