Giải Toán lớp 10 trang 24 tập 2 Kết nối tri thức với cuộc sống giúp các bạn học sinh có thêm nhiều gợi ý tham khảo để trả lời các câu hỏi bài tập trong SGK bài 17 Dấu của tam thức bậc hai thuộc chương 6 Hàm số, đồ thị và ứng dụng.
Bạn đang đọc: Toán 10 Bài 17: Dấu của tam thức bậc hai
Toán 10 Kết nối tri thức trang 24 được biên soạn với các lời giải chi tiết, đầy đủ và chính xác bám sát chương trình sách giáo khoa môn Toán lớp 10. Giải Toán lớp 10 trang 24 Kết nối tri thức tập 2 sẽ là tài liệu cực kì hữu ích hỗ trợ các em học sinh trong quá trình giải bài tập. Đồng thời phụ huynh có thể sử dụng để hướng dẫn con em học tập và đổi mới phương pháp giải phù hợp hơn. Vậy sau đây là trọn bộ bài giải Toán 10 bài 17: Dấu của tam thức bậc hai mời các bạn cùng theo dõi.
Giải Toán 10 Bài 17: Dấu của tam thức bậc hai
Trả lời câu hỏi phần Mở đầu Toán 10 bài 17
Xét bài toán rào vườn ở Bài 16, nhưng ta trả lời câu hỏi: Hai cột góc hàng rào (H.6.8) cần phải cắm cách bờ tường bao nhiêu mét để mảnh đất được rào chắn có diện tích không nhỏ hơn 48 m2 ?
Gợi ý đáp án
Theo Bài 16, diện tích mảnh đất được rào chắn là S(x) = – 2x2+ 20x (m2).
Vì mảnh đất được rào chắn có diện tích không nhỏ hơn 48 m2 nghĩa là S(x) phải lớn hơn hoặc bằng 48.
Khi đó: – 2x2 + 20x ≥ 48 ⇔ 2x2 – 20x + 48 ≤ 0 (1).
Ta cần giải bất phương trình (1).
Sau bài học này ta sẽ giải được bất phương trình (1) như sau:
Tam thức bậc hai f(x) = 2x2 – 20x + 48 có hai nghiệm x1 = 4; x2 = 6 và hệ số a = 2 > 0. Từ đó suy ra tập nghiệm của bất phương trình (1) là đoạn [4; 6]. Như vậy khoảng cách từ điểm cắm cột đến bờ tường phải lớn hơn hoặc bằng 4 m và nhỏ hơn hoặc bằng 6 m thì mảnh đất rào chắn của bác Việt sẽ có diện tích không nhỏ hơn 48 m2.
Giải Toán 10 Bài 17 phần Hoạt động
Hoạt động 1
Hãy chỉ ra một vài đặc điểm chung của các biểu thức dưới đây:
A = 0,5x2;
B = 1 – x2;
C = x2 + x + 1;
D = (1 – x)(2x + 1).
Gợi ý đáp án
Ta có: A = 0,5x2 = 0,5x2 + 0x + 0;
B = 1 – x2 = – x2 + 0x + 1;
C = x2 + x + 1;
D = (1 – x)(2x + 1) = 2x + 1 – 2x2 – x = – 2x2 + x + 1.
Các biểu thức trên đều có dạng ax2 + bx + c, trong đó a, b, c là các số thực và a ≠ 0.
Hoạt động 2
Cho hàm số bậc hai y = f(x) = x2 – 4x + 3.
a) Xác định hệ số a. Tính f(0), f(1), f(2), f(3), f(4) và nhận xét về dấu của chúng so với dấu của hệ số a.
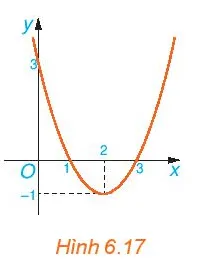
b) Cho đồ thị hàm số y = f(x) (H.6.17). Xét trên từng khoảng (– ∞; 1), (1; 3), (3; +∞), đồ thị nằm phía trên hay nằm phía dưới trục Ox?
c) Nhận xét về dấu của f(x) và dấu của hệ số a trên từng khoảng đó.
Gợi ý đáp án
a) Hàm số bậc hai y = f(x) = x2 – 4x + 3.
Hệ số a = 1 > 0.
Ta có: f(0) = 02 – 4 . 0 + 3 = 3 > 0, f(0) cùng dấu với hệ số a.
f(1) = 12 – 4 . 1 + 3 = 0, f(1) không mang dấu.
f(2) = 22 – 4 . 2 + 3 = – 1
f(3) = 32 – 4 . 3 + 3 = 0, f(3) không mang dấu.
f(4) = 42 – 4 . 4 + 3 = 3 > 0, f(4) cùng dấu với hệ số a.
b) Quan sát đồ thị H.6.17, ta thấy:
+ Trên các khoảng (– ∞; 1) và (3; +∞), đồ thị hàm số nằm hoàn toàn phía trên trục Ox.
+ Trên khoảng (1; 3), đồ thị hàm số nằm hoàn toàn phía dưới trục Ox.
c) Khi đồ thị hàm số nằm hoàn toàn trên trục Ox thì f(x) > 0, ngược lại khi đồ thị hàm số nằm hoàn toàn phía dưới trục Ox thì f(x)
Hệ số a = 1 > 0.
Vậy trên các khoảng (– ∞; 1) và (3; +∞), f(x) cùng dấu với hệ số a; trên khoảng (1; 3), f(x) trái dấu với hệ số a.
Giải Toán 10 trang 24 Kết nối tri thức – Tập 2
Bài 6.15 trang 24
Xét dấu các tam thức bậc hai sau:
Gợi ý đáp án
 0, a>0,” width=”297″ height=”24″ data-type=”0″ data-latex=”a. f(x) = 3x^{2}-4x+1, Delta >0, a>0,” data-src=”https://tex.vdoc.vn?tex=a.%20f(x)%20%3D%203x%5E%7B2%7D-4x%2B1%2C%20%5CDelta%20%3E0%2C%20a%3E0%2C”> có 2 nghiệm phân biệt lần lượt là 1 và
0, a>0,” width=”297″ height=”24″ data-type=”0″ data-latex=”a. f(x) = 3x^{2}-4x+1, Delta >0, a>0,” data-src=”https://tex.vdoc.vn?tex=a.%20f(x)%20%3D%203x%5E%7B2%7D-4x%2B1%2C%20%5CDelta%20%3E0%2C%20a%3E0%2C”> có 2 nghiệm phân biệt lần lượt là 1 và
Bảng xét dấu:

Vậy f(x) > 0 với mọi và f(x)
b.  0″ width=”264″ height=”24″ data-type=”0″ data-latex=”f(x)=x^{2}+2x+1, Delta =0, a>0″ data-src=”https://tex.vdoc.vn?tex=f(x)%3Dx%5E%7B2%7D%2B2x%2B1%2C%20%5CDelta%20%3D0%2C%20a%3E0″>, có nghiệm kép x = -1.
0″ width=”264″ height=”24″ data-type=”0″ data-latex=”f(x)=x^{2}+2x+1, Delta =0, a>0″ data-src=”https://tex.vdoc.vn?tex=f(x)%3Dx%5E%7B2%7D%2B2x%2B1%2C%20%5CDelta%20%3D0%2C%20a%3E0″>, có nghiệm kép x = -1.
Vậy f(x) > 0 với mọi
 0, a0, a có 2 nghiệm phân biệt lần lượt là 1 và 2.
0, a0, a có 2 nghiệm phân biệt lần lượt là 1 và 2.
Bảng xét dấu:

Vậy f(x) 0″ width=”273″ height=”22″ data-type=”0″ data-latex=”xin left ( -infty ;1 right )cup left ( 2;+infty right ) và f(x) > 0″ data-src=”https://tex.vdoc.vn?tex=x%5Cin%20%5Cleft%20(%20-%5Cinfty%20%3B1%20%5Cright%20)%5Ccup%20%5Cleft%20(%202%3B%2B%5Cinfty%20%5Cright%20)%20v%C3%A0%20f(x)%20%3E%200″> với mọi
. Suy ra f(x) luôn âm với mọi số thực x.
Bài 6.16 trang 24
Giải các bất phương trình bậc hai:
Gợi ý đáp án
a. có
 0″ width=”50″ height=”17″ data-type=”0″ data-latex=”Delta >0″ data-src=”https://tex.vdoc.vn?tex=%5CDelta%20%3E0″>, a>0, 2 nghiệm phân biệt lần lượt là -1 và 1.
0″ width=”50″ height=”17″ data-type=”0″ data-latex=”Delta >0″ data-src=”https://tex.vdoc.vn?tex=%5CDelta%20%3E0″>, a>0, 2 nghiệm phân biệt lần lượt là -1 và 1.
Vậy tập nghiệm là
b. có
, a>0, nghiệm kép là
 0″ width=”211″ height=”22″ data-type=”0″ data-latex=”x = -1, có x^{2}-2x-1>0″ data-src=”https://tex.vdoc.vn?tex=x%20%3D%20-1%2C%20c%C3%B3%20x%5E%7B2%7D-2x-1%3E0″> với mọi
0″ width=”211″ height=”22″ data-type=”0″ data-latex=”x = -1, có x^{2}-2x-1>0″ data-src=”https://tex.vdoc.vn?tex=x%20%3D%20-1%2C%20c%C3%B3%20x%5E%7B2%7D-2x-1%3E0″> với mọi
Nên bất phương trình vô nghiệm.
Vậy bất phương trình vô nghiệm.
 0, a0, a nghiệm phân biệt lần lượt là
0, a0, a nghiệm phân biệt lần lượt là và
Vậy tập nghiệm là
 0 nên 5x^{2}+x+1 >0″ width=”386″ height=”22″ data-type=”0″ data-latex=”d. 5x^{2}+x+1 có Delta 0 nên 5x^{2}+x+1 >0″ data-src=”https://tex.vdoc.vn?tex=d.%205x%5E%7B2%7D%2Bx%2B1%20c%C3%B3%20%5CDelta%20%3C0%2C%20a%3E0%20n%C3%AAn%205x%5E%7B2%7D%2Bx%2B1%20%3E0″> với mọi số thực x.
0 nên 5x^{2}+x+1 >0″ width=”386″ height=”22″ data-type=”0″ data-latex=”d. 5x^{2}+x+1 có Delta 0 nên 5x^{2}+x+1 >0″ data-src=”https://tex.vdoc.vn?tex=d.%205x%5E%7B2%7D%2Bx%2B1%20c%C3%B3%20%5CDelta%20%3C0%2C%20a%3E0%20n%C3%AAn%205x%5E%7B2%7D%2Bx%2B1%20%3E0″> với mọi số thực x.
Vậy tập nghiệm là
Bài 6.17 trang 24
Tìm các giá trị của tham số m để tam thức bậc hai sau dương với mọi
Gợi ý đáp án
 0″ width=”230″ height=”24″ data-type=”0″ data-latex=”x^{2}+(m+1)x+2m+3>0″ data-src=”https://tex.vdoc.vn?tex=x%5E%7B2%7D%2B(m%2B1)x%2B2m%2B3%3E0″> với mọi
0″ width=”230″ height=”24″ data-type=”0″ data-latex=”x^{2}+(m+1)x+2m+3>0″ data-src=”https://tex.vdoc.vn?tex=x%5E%7B2%7D%2B(m%2B1)x%2B2m%2B3%3E0″> với mọi
 0end{matrix}right.Leftrightarrow m^{2}-6m-110end{matrix}right.Leftrightarrow m^{2}-6m-11
0end{matrix}right.Leftrightarrow m^{2}-6m-110end{matrix}right.Leftrightarrow m^{2}-6m-11
Bài 6.18 trang 24
Một vật được ném theo phương thẳng đứng xuống dưới từ độ cao 320 m với vận tốc ban đầu vQ = 20m/s. Hỏi sau ít nhất bao nhiêu giấy, vật đó cách mặt đất không quá 100m? Giả thiết rằng sức cản của không khí là không đáng kể.
Gợi ý đáp án
Chọn trục Oy thẳng đứng, chiều dương hướng xuống, gốc tọa độ O tại điểm ném và gốc thời gian là lúc ném.
có, với g là gia tốc tự do, lấy g = 10
Nếu vật cách mặt đất 100m thì quãng đường vật đã đi được là y = 320 – 100 = 220 m.
Để vật đó cách mặt đất không quá 100m, thì quãng đường y đi được của vật phải lớn hơn 220.
Ta có bất phương trình: 220″ width=”125″ height=”20″ data-type=”0″ data-latex=”20t+5t^{2}>220″ data-src=”https://tex.vdoc.vn?tex=20t%2B5t%5E%7B2%7D%3E220″>
220″ width=”125″ height=”20″ data-type=”0″ data-latex=”20t+5t^{2}>220″ data-src=”https://tex.vdoc.vn?tex=20t%2B5t%5E%7B2%7D%3E220″>
 0″ width=”181″ height=”20″ data-type=”0″ data-latex=”Leftrightarrow 5t^{2}+20t-220>0″ data-src=”https://tex.vdoc.vn?tex=%5CLeftrightarrow%205t%5E%7B2%7D%2B20t-220%3E0″>
0″ width=”181″ height=”20″ data-type=”0″ data-latex=”Leftrightarrow 5t^{2}+20t-220>0″ data-src=”https://tex.vdoc.vn?tex=%5CLeftrightarrow%205t%5E%7B2%7D%2B20t-220%3E0″>
 -2+4sqrt{3}approx 4,93″ width=”197″ height=”23″ data-type=”0″ data-latex=”Leftrightarrow t>-2+4sqrt{3}approx 4,93″ data-src=”https://tex.vdoc.vn?tex=%5CLeftrightarrow%20t%3E-2%2B4%5Csqrt%7B3%7D%5Capprox%204%2C93″> hoặc
-2+4sqrt{3}approx 4,93″ width=”197″ height=”23″ data-type=”0″ data-latex=”Leftrightarrow t>-2+4sqrt{3}approx 4,93″ data-src=”https://tex.vdoc.vn?tex=%5CLeftrightarrow%20t%3E-2%2B4%5Csqrt%7B3%7D%5Capprox%204%2C93″> hoặc (loại)
Vậy sau ít nhất 4,93 giấy thì vật đó cách mặt đất không quá 100m.
Bài 6.19 trang 24
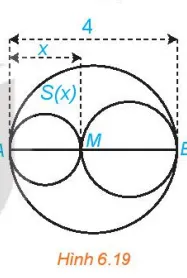
Xét đường tròn đường kính AB = 4 và một điểm M di chuyển trên đoạn AB, đặt AM = x. Xét hai đường tròn đường kính AM và MB. Kí hiệu S(x) là diện tích phần hình phẳng nằm trong hình tròn lớn và nằm ngoài hai hình tròn nhỏ. Xác định các giá trị của x để diện tích S(x) không vượt quá một nửa tổng diện tích hai hình tròn nhỏ.
Gợi ý đáp án
AM = x, AB = 4 => MB = 4 -x, nên bán kính đường tròn đường kính AM là , bán kính đường tròn đường kính MB là
Diện tích hình tròn đường kính AM là:
Diện tích hình tròn đường kính MB là:
Diện tích hình tròn đường kính AB là:
Diện tích
Theo đề bài S(x)
Mà x > 0 nên ta có: