Giải Toán lớp 7 bài 11: Định lí và chứng minh định lí bao gồm đáp án chi tiết cho từng phần, từng bài tập trong SGK Toán 7 Tập 1 Kết nối tri thức với cuộc sống trang 55, 56, 57.
Bạn đang đọc: Toán 7 Bài 11: Định lí và chứng minh định lí
Lời giải Toán 7 Bài 11 Kết nối tri thức trình bày khoa học, biên soạn dễ hiểu, giúp các em nâng cao kỹ năng giải Toán 7, từ đó học tốt môn Toán lớp 7 hơn. Đồng thời, cũng giúp thầy cô nhanh chóng soạn giáo án Bài 11 Chương III – Góc và đường thẳng song song. Vậy mời thầy cô và các em cùng theo dõi bài viết dưới đây của Download.vn:
Giải Toán 7 bài 11: Định lí và chứng minh định lí sách Kết nối tri thức với cuộc sống
Giải Toán 7 Kết nối tri thức với cuộc sống tập 1 bài 11 – Luyện tập
Luyện tập 1
Vẽ hình và viết giả thiết, kết luận của định lí: “hai góc đối đỉnh thì bằng nhau”.
Gợi ý đáp án:
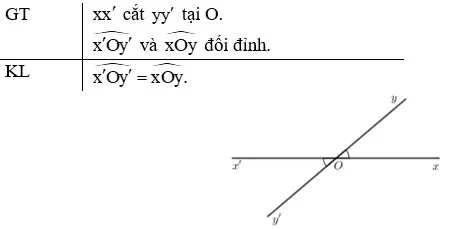
Luyện tập 2
Em hãy chứng minh định lí: “Hai góc kề bù bằng nhau thì mỗi góc là một góc vuông”.
Gợi ý đáp án:
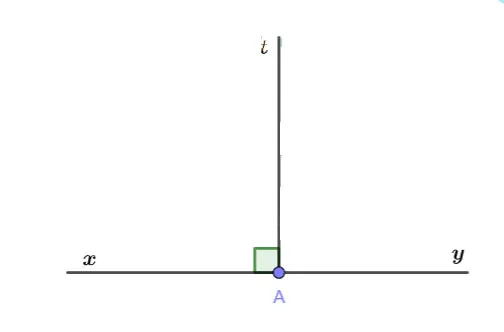
|
Giải thiết |
|
|
Kết luận |
Chứng minh
Theo bài ra ta có:
xAt và tAy là hai góc kề bù
=>
Mặt khác hai góc kề bù đã cho bằng nhau
=>
=>
Vậy mỗi góc có số đo là 900 hay mỗi góc là một góc vuông.
Giải Toán 7 Kết nối tri thức với cuộc sống trang 57 tập 1
Bài 3.24
Có thể coi định lí “Hai đường thẳng phân biệt cùng vuông góc với một đương thẳng thứ ba thì chúng song song với nhau” được suy ra trực tiếp từ định lí về dấu hiệu nhận biết hai đường thẳng song song không? Suy ra như thế nào?
Gợi ý đáp án:
Định lí: “Hai đường thẳng phân biệt cùng vuông góc với một đương thẳng thứ ba thì chúng song song với nhau”
Hình vẽ minh họa:
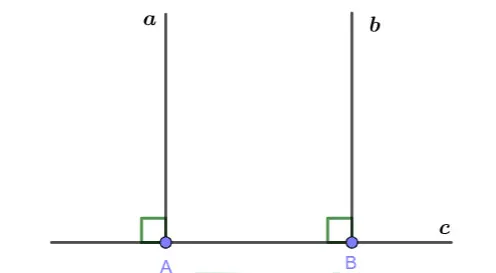
|
Giải thiết |
c vuông góc với b, c vuông góc với a, c cắt a tại A, c cắt b tại B |
|
Kết luận |
a // b |
Chứng minh
Ta có: c vuông góc với a =>
c vuông góc với b =>
=>
Do hai góc ở vị trí đồng vị nên a // b
Bài 3.25
Hãy chứng minh định lí nói ở Ví dụ trang 56: “Một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó cũng vuông góc với đường thẳng còn lại”. Trong chứng minh đó ta đã sử dụng những điều đúng đã biết nào?
Gợi ý đáp án:
Hình vẽ minh họa:

|
Giải thiết |
a // b, c vuông góc với a, c cắt a tại A, c cắt b tại B |
|
Kết luận |
c vuông góc với b |
Chứng minh
Ta có: c vuông góc với a =>
Mặt khác a // b => (Hai góc ở vị trí đồng vị)
=> c vuông góc với b
Bài 3.26
Cho góc xOy không phải là góc bẹt. Khẳng định nào sau đây đúng?
(1) Nếu Ot là tia phân giác của góc xOy thì
(2) Nếu tia Ot thỏa mãn thì Ot là tia phân giác của góc xOy.
Nếu có khẳng định không đúng, hãy nêu ví dụ cho thấy khẳng định đó không đúng. Gợi ý: Xét tia đối của một tia phân giác.
Gợi ý đáp án:
(1) đúng vì Ot là tia phân giác của góc xOy thì
(2) sai vì
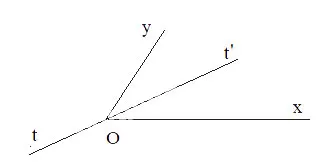
Ta có: nhưng Ot không là tia phân giác của góc xOy
Xét tia Ot’ là tia đối của tia Ot thì Ot’ là tia phân giác của góc xOy.
Chú ý:
Mỗi góc khác góc bẹt chỉ có một tia phân giác.

