Giải Toán lớp 6 Luyện tập chung trang 20, 21 bao gồm đáp án chi tiết cho từng phần, từng bài tập trong SGK Toán 6 Tập 1 Kết nối tri thức với cuộc sống.
Bạn đang đọc: Toán 6 Luyện tập chung trang 20
Với lời giải chi tiết, trình bày khoa học, được biên soạn dễ hiểu, giúp các em nâng cao kỹ năng giải Toán 6, từ đó học tốt môn Toán lớp 6 hơn. Đồng thời, cũng giúp thầy cô nhanh chóng soạn giáo án Luyện tập chung trang 20 Chương I: Tập hợp các số tự nhiên. Mời thầy cô và các em cùng theo dõi bài viết dưới đây của Download.vn:
Giải Toán 6 Luyện tập chung trang 20 sách Kết nối tri thức với cuộc sống
Giải Toán 6 Kết nối tri thức với cuộc sống trang 21 tập 1
Bài 1.31
Gọi A là tập hợp các số tự nhiên lớn hơn 3 và không lớn hơn 7.
a) Viết tập hợp A bằng hai cách: Liệt kê phần tử và nêu dấu hiệu đặc trưng cho các phần tử.
b) Trong các số tự nhiên nhỏ hơn 10, những số nào không phải là phần tử của tập hợp A?
Hướng dẫn giải:
Để cho một tập hợp, thường có hai cách:
a) Liệt kê các phần tử của tập hợp là viết các phần tử của tập hợp trong dấu ngoặc { } theo thứ tự tùy ý nhưng mỗi phần tử chỉ được viết một lần.
b) Chỉ ra tính chất đặc trưng cho các phần tử của tập hợp.
Gợi ý đáp án:
a) Viết tập hợp A bằng hai cách:
A = {4; 5; 6; 7}
A = {n ∈ N | 3
b) Trong các số tự nhiên nhỏ hơn 10, những số không phải là phần tử của tập hợp A là các số nhỏ hơn 3 và lớn hơn 7.
Tập hợp các số đó là: B = {0; 1; 2; 3; 8; 9}
Bài 1.32
a) Viết số tự nhiên nhỏ nhất có bốn chữ số.
b) Viết số tự nhiên nhỏ nhất có bốn chữ số khác nhau
c) Viết số tự nhiên nhỏ nhất có bốn chữ số khác nhau và đều là số chẵn
d) Viết số tự nhiên nhỏ nhất có bốn chữ số khác nhau và đều là số lẻ
Gợi ý đáp án:
a) Số tự nhiên nhỏ nhất có bốn chữ số: 1000
b) Số tự nhiên nhỏ nhất có bốn chữ số khác nhau: 1023
c) Số tự nhiên nhỏ nhất có bốn chữ số khác nhau và đều là số chẵn:2046
d) Số tự nhiên nhỏ nhất có bốn chữ số khác nhau và đều là số lẻ: 1357
Bài 1.33
Ta đã biết: Giá trị của mỗi chữ số của một số tự nhiên trong hệ thập phân phụ thuộc vào vị trí của nó. Chẳng hạn, chữ số 2 có giá trị bằng 2 nếu nó nằm ở hàng đơn vị, có giá trị bằng 20 nếu nó nằm ở hàng chục,… Tuy nhiên có một chữ số mà giá trị của nó không thay đổi dù nó nằm ở bất kì vị trí nào, đó là chữ số nào?
Hướng dẫn giải
Ví dụ: Số 3521:
Chữ số 1 có giá trị bằng 1
Chữ số 2 có giá trị bằng 20
Chữ số 5 có giá trị bằng 500
Chữ số 3 có giá trị bằng 3000
Gợi ý đáp án:
Chữ số cần tìm là chữ số 0. Bởi vì 0 nhân với bất kì số nào cũng bằng 0.
Bài 1.34
Một xe ô tô chở 30 bao gạo và 40 bao ngô. Biết rằng mỗi bao gạo nặng 50kg, mỗi bao ngô nặng 60kg. Hỏi xe ô tô chở tất cả bao nhiêu kilôgam gạo và ngô?
Gợi ý đáp án:
Cách 1:
30 bao gạo nặng số kilôgam là: 30 . 50 = 1500 (kg)
40 bao ngô nặng số kilôgam là: 40 . 60 = 2400 (kg)
Xe ô tô chở tất cả số kilôgam gạo và ngô là: 1500 + 2400 = 3900 (kg)
Cách 2:
Số kilôgam gạo xe ô tô chở là:
30 . 50 = 1 500 (kg)
Số kilôgam ngô xe ô tô chở là:
40 . 60 = 2 400 (kg)
Vậy xe ô tô chở tất cả số kilôgam gạo và ngô là:
1 500 + 2 400 = 3 900 (kg)
Đáp số: 3 900 kg
Bài 1.35
Trong tháng 7 nhà ông Khánh dùng hết 115 số điện. Hỏi ông Khánh phải trả bao nhiêu tiền điện, biết đơn giá điện như sau:
Giá tiền cho 50 số đầu tiên là 1 678 đồng/số
Giá tiền cho 50 số tiếp theo (từ số 51 đến số 100) là 1 734 đồng/số
Giá tiền cho 100 số tiếp theo (từ số 101 đến số 200) là 2 014 đồng/số
Gợi ý đáp án:
Số tiền phải trả cho 50 số điện đầu tiên là:
50 . 1 678 = 83 900 (đồng)
Số tiền phải trả từ số 51 đến số 100 là:
50 . 1 734 = 86 700 (đồng)
Số tiền phải trả từ số 101 đến 115 là:
15 . 2 014 = 30 210 (đồng)
Vậy ông Khánh phải trả số tiền:
83 900 + 86 700 + 30 210 = 200 810 (đồng)
Lý thuyết Luyện tập chung trang 20
1. Phép cộng và phép trừ số tự nhiên
a) Phép cộng số tự nhiên
+ Phép cộng hai số tự nhiên a và b cho ta một số tự nhiên gọi là tổng của chúng, kí hiệu là a + b.
Có thể minh họa phép cộng nhờ tia số, chẳng hạn phép cộng 3 + 4 = 7
Ví dụ 1: Tính:
a) 3 + 4;
b) 23 + 37;
c) 78 + 189.
Lời giải
a) 3 + 4 = 7;
b) 23 + 37 = 60;
c) 78 + 189 = 267.
+ Phép cộng số tự nhiên có các tính chất:
- Giáo hoán: a + b = b + a.
- Kết hợp: (a + b) + c = a + (b + c).
+ Chú ý: a + 0 = 0 + a = a.
+ Tổng (a + b) + c hay a + (b + c) gọi là tổng của ba số a, b, c và viết gọn là: a + b + c.
Ví dụ 2. Tính:
a) 7 + 12 + 13;
b) 25 + 89 + 75 + 11.
Lời giải
a) 7 + 12 + 13 = 12 + (7 + 13) = 12 + 20 = 32;
b) 25 + 89 + 75 + 11 = (25 + 75) + (89 + 11) = 100 + 100 = 200.
b. Phép trừ số tự nhiên
+ Với hai số tự nhiên a, b đã cho, nếu có số tự nhiên c sao cho a + b = c thì ta có phép trừ
a – b = c. Trong đó, a là số bị trừ, b là số trừ và c là hiệu.
Ví dụ 3. Tính:
a) 725 – 630;
b) 429 – 236.
Lời giải
a) 725 – 630 = 95.
b) 419 – 236 = 183.
2. Phép nhân và phép chia số tự nhiên
+ Phép nhân hai số tự nhiên a và b cho ta một số tự nhiên c được gọi là tích.
Kí hiệu: a.b = c (hoặc a x b = c)
Trong đó: a và b là hai thừa số, c là tích.
+ Chú ý: Nếu các thừa số đều bằng chữ, hoặc chỉ có một thừa số bằng số thì ta có thể không nhân giữa các thừa số. Chẳng hạn: x.y = xy; 5.m = 5m; …
Ví dụ 1. Tính:
a) 254.35;
b) 86.72.
Lời giải
a)

Vậy 254.35 = 8 890.
b)
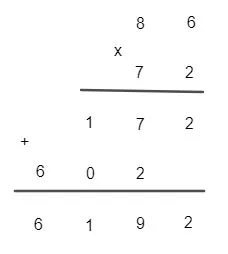
Vậy 86.72 = 6 192.
+ Tính chất của phép nhân:
– Giao hoán: ab = ba.
– Kết hợp: (ab)c = a(bc).
– Phân phối của phép nhân với phép cộng: a(b + c) = ab + ac.
Ví dụ 2. Thực hiện phép tính:
a) 125.3 542.8;
b) 69.73 + 69.27.
Lời giải
a) 125.3 542.8
= (125.8).3 542
= 1 000. 3 542
= 3 542 000.
b) 69.73 + 69.27
= 69.(73 + 27)
= 69.100
= 6 900.
+ Với hai số tự nhiên a và b đã cho (b khác 0), ta luôn tìm được đúng hai số tự nhiên q và r sao cho a = b.q + r, trong đó 0 ≤ r ≤ b.
Nếu r = 0 thì ta có phép chia hết a:b = q; a là số bị chia, b là số chia, q là thương.
Nếu r ≠ 0 thì ta có phép chia có dư a:b = q (dư r); a là số bị chia, b là số chia, q là thương, r là số dư.

