Tam giác cân: Khái niệm, tính chất, cách chứng minh và bài tập

Tam giác cân là một loại tam giác có ít nhất hai cạnh bằng nhau và hai góc ở đáy cân bằng nhau.

Bạn đang đọc: Tam giác cân: Khái niệm, tính chất, cách chứng minh và bài tập

Tam giác cân là một loại hình học trọng tâm trong chương trình Toán 7. Tính chất đặc biệt của tam giác cân là hai cạnh bên bằng nhau và hai góc ở đáy cũng bằng nhau. Chính vì thế tạo ra một sự cân đối và đẹp mắt trong hình học. Vậy công thức tính diện tích tam giác cân như thế nào? Tính chất tam giác cân là gì? Mời các bạn cùng theo dõi bài viết dưới đây của Download.vn. Bên cạnh đó các bạn xem thêm tài liệu: cách vẽ hình chiếu, tâm đường tròn ngoại tiếp tam giác.

Tổng hợp kiến thức về tam giác cân

1. Định nghĩa tam giác cân

Tam giác cân là tam giác có hai cạnh bằng nhau, hai cạnh này được gọi là hai cạnh bên. Đỉnh của một tam giác cân là giao điểm của hai cạnh bên. Góc được tạo bởi đỉnh được gọi là góc ở đỉnh, hai góc còn lại gọi là góc ở đáy.

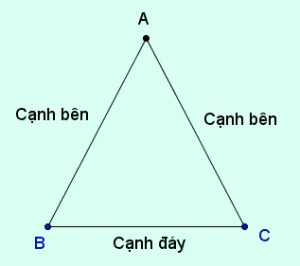
Ở hình trên, tam giác ABC có AB = AC suy ra tam giác ABC cân.

Có AB và AC là hai cạnh bên nên tam giác ABC cân tại đỉnh A.

2. Tính chất tam giác cân

Tam giác cân có 4 tính chất sau đây:

Tính chất 1: Trong một tam giác cân hai góc ở đáy bằng nhau.

Chứng minh:

Giả thiết	Tam giác ABC cân tại A, AB = AC
Kết luận

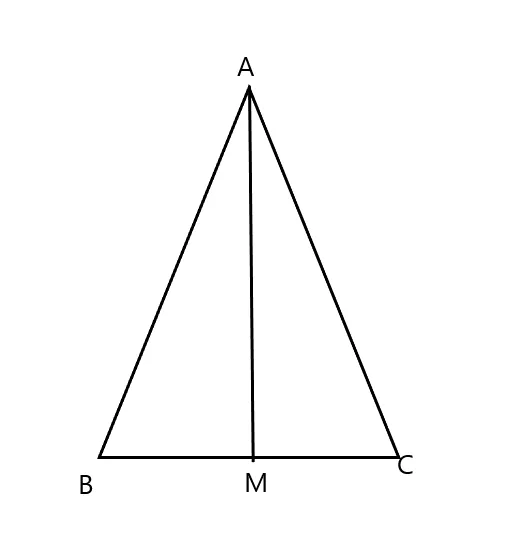
Trong tam giác cân ABC, gọi AM là tia phân giác của góc

Khi đó ta có

Xét tam giác ABM và tam giác ACM có:

AB = AC (gt)

(cmt)

AM chung

Suy ta ΔABM = ΔACM (c.g.c) (đpcm)

Tính chất 2: Một tam giác có hai góc bằng nhau thì là tam giác cân.

Chứng minh

Giả thiết	Tam giác ABC,
Kết luận	Tam giác ABC cân tại A

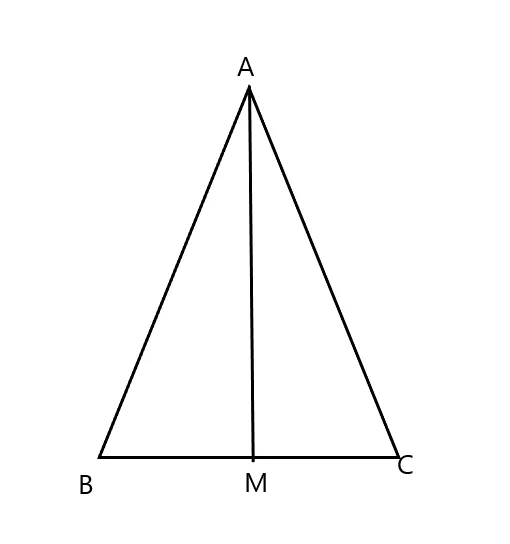
Trong tam giác ABC, gọi AM là tia phân giác của

Tam giác ABM có (tổng 3 góc trong một tam giác)

Tam giác ACM có (tổng 3 góc trong một tam giác)

Mà lại có

nên

Xét tam giác ABM và tam giác ACM có:

Suy ra ΔABM = ΔACM (g – g – g) nên AB = AC (cạnh tương ứng bằng nhau)

Xét tam giác ABC có AB = AC, suy ra tam giác ABC cân tại A (định nghĩa)

Tính chất 3: Trong một tam giác cân, đường trung trực ứng với cạnh đáy đồng thời là đường phân giác, đường trung tuyến, đường cao của tam giác đó.

Tính chất 4: Trong một tam giác, nếu có một đường trung tuyến đồng thời là đường trung trực thì tam giác là tam giác cân.

3. Dấu hiệu nhận biết tam giác cân

Trong tam giác cân có 2 dấu hiệu nhận biết đó là:

• Dấu hiệu 1: Nếu một tam giác có hai cạnh bên bằng nhau thì tam giác đó là tam giác cân.
• Dấu hiệu 2: Nếu một tam giác có hai góc bằng nhau thì tam giác đó là tam giác cân.

4. Diện tích tam giác cân

Diện tích tam giác cân bằng Tích của chiều cao nối từ đỉnh tam giác đó tới cạnh đáy tam giác, sau đó chia cho 2.

– Công thức tính diện tích tam giác cân: S = (a x h)/ 2

Trong đó:

• a: Chiều dài đáy tam giác cân (đáy là một trong 3 cạnh của tam giác)
• h: Chiều cao của tam giác (chiều cao tam giác bằng đoạn thẳng hạ từ đỉnh xuống đáy).

5. Cách chứng minh tam giác cân

– Cách 1: Chứng minh tam giác đó có hai cạnh bằng nhau.

– Cách 2: Chứng minh tam giác đó có hai góc bằng nhau.

Ví dụ 1: Trong tam giác ABC có Δ ABD = Δ ACD . Chứng minh tam giác ABC cân.

+ Chứng minh theo cách 1:

Theo bài ra, ta có:

Δ ABD = Δ ACD

=> AB = AC

=> Tam giác ABC cân tại A

+ Chứng minh theo cách 2:

Theo bài ra, ta có:

∆ ABD = ∆ ACD

=> Góc B = C

=> Tam giác ABC cân tại A

Ví dụ 2: 

Cho tam giác ABC cân tại A. Lấy điểm D thuộc cạnh AC, điểm E thuộc cạnh AB sao cho AD = AE

a) So sánh góc ABD và ACE

b) Gọi I là giao điểm của BD và CE. ΔIBC là tam giác gì ? Vì sao ?

Gợi ý đáp án

a) Tam giác ABC cân tại A (giả thiết)

Xét ΔABD và ΔACE có:

AB = AC (giả thiết)

chung

AD = AE (giả thiết)

⇒ ΔABD = ΔACE (cạnh – góc – cạnh)

⇒ (cặp góc tương ứng)

b) ΔIBC có:

⇒ ΔIBC cân tại I

Ví dụ 3: Cho tam giác ABC cân tại A và các điểm E, F lần lượt nằm trên các cạnh AC, AB sao cho BE vuông góc với AC, CF vuông góc với AB (H.4.69). Chứng minh rằng BE = CF.

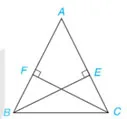
Gợi ý đáp án:

Do tam giác ABC cân tại A nên: (tính chất tam giác cân)

Xét 2 tam giác vuông BFC và CEB:

BC chung

Delta BFC = Delta CEB” width=”174″ height=”17″ data-type=”0″ data-latex=”=>Delta BFC = Delta CEB” data-src=”https://tex.vdoc.vn?tex=%3D%3E%5CDelta%20BFC%20%3D%20%5CDelta%20CEB”>(cạnh huyền – góc nhọn)

=>BE=CF (2 cạnh tương ứng).

Ví dụ 4

Cho tam giác ABC cân tại A và M là trung điểm của đoạn thẳng BC. Chứng minh AM vuông góc với BC và AM là tia phân giác của góc BAC.

Gợi ý đáp án:

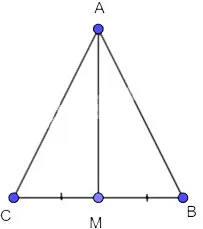
Xét 2 tam giác AMC và AMB có:

AM chung

AB=AC (do tam giác ABC cân tại A)

MB=MC (gt)

(2 góc tương ứng)

là phân giác của góc BAC

Mặt khác:(2 góc tương ứng) mà (2 góc kề bù)

Nên: .

Vậy AM vuông góc với BC.

Ví dụ 5

Cho tam giác ABC và M là trung điểm của đoạn thẳng BC.

a) Giả sử AM vuông góc với BC. Chứng minh rằng tam giác ABC cân tại A.

b) Giả sử AM là tia phân giác của góc BAC. Chứng minh rằng tam giác ABC cân tại A.

Gợi ý đáp án:

a)

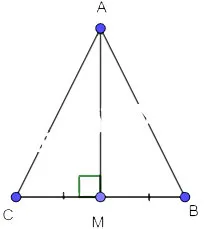
Xét 2 tam giác vuông AMC và AMB có:

AM chung

BM=CM (gt)

Delta AMB = Delta AMC (c.g.c)” width=”241″ height=”22″ data-type=”0″ data-latex=”=>Delta AMB = Delta AMC (c.g.c)” data-src=”https://tex.vdoc.vn?tex=%3D%3E%5CDelta%20AMB%20%3D%20%5CDelta%20AMC%20(c.g.c)”>

=> AM=BM (2 cạnh tương ứng)

=> Tam giác ABM cân tại A

b)

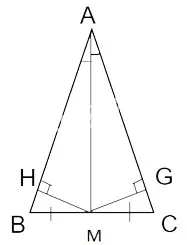
Kẻ MH vuông góc với AB (H thuộc AB)

MG vuông góc với AC (G thuộc AC)

Xét 2 tam giác vuông AHM và AGC có:

AM chung

Delta AHM = Delta AGC” width=”183″ height=”17″ data-type=”0″ data-latex=”=>Delta AHM = Delta AGC” data-src=”https://tex.vdoc.vn?tex=%3D%3E%5CDelta%20AHM%20%3D%20%5CDelta%20AGC”>(cạnh huyền – góc nhọn)

=> HM=GM (2 cạnh tương ứng)

Xét 2 tam giác vuông BHM và CGM có:

BM=CM(gt)

MH=MG(cmt)

Delta BHM = Delta CGM” width=”188″ height=”17″ data-type=”0″ data-latex=”=>Delta BHM = Delta CGM” data-src=”https://tex.vdoc.vn?tex=%3D%3E%5CDelta%20BHM%20%3D%20%5CDelta%20CGM”>(cạnh huyền – cạnh góc vuông)

widehat {BMH} = widehat {CMH}” width=”159″ height=”23″ data-type=”0″ data-latex=”=>widehat {BMH} = widehat {CMH}” data-src=”https://tex.vdoc.vn?tex=%3D%3E%5Cwidehat%20%7BBMH%7D%20%3D%20%5Cwidehat%20%7BCMH%7D”>(2 góc tương ứng)

=>Tam giác ABC cân tại A.

Ví dụ 6

Tam giác vuông có hai cạnh bằng nhau được gọi là tam giác vuông cân.

Hãy giải thích các khẳng định sau:

a) Tam giác vuông cân thì cân tại đỉnh góc vuông;

b) Tam giác vuông cân có hai góc nhọn bằng 45°;

c) Tam giác vuông có một góc nhọn bằng 45° là tam giác vuông cân.

Gợi ý đáp án:

a) Do tổng ba góc trong 1 tam giác bằng 180 độ nên tam giác không thể có 2 góc vuông

=>Tam giác vuông cân sẽ có 2 góc nhọn bằng nhau

=> Tam giác vuông cân thì cân tại đỉnh góc vuông.

b) Giả sử hai góc nhọn trong tam giác vuông là x, ta có:

Vậy tam giác vuông cân có hai góc nhọn bằng 45°.

c) Gọi góc còn lại của tam giác vuông có 1 góc nhọn bằng 45° là x, ta có:

Vậy tam giác vuông có một góc nhọn bằng 45° là tam giác vuông cân.

Ví dụ 7

Cho hình 14, biết ED = EF và EI là tia phân giác của.

Chứng minh rằng:

a.

b. Tam giác DIF cân.

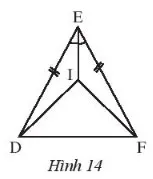
Gợi ý đáp án:

a. Xét và có:

EI chung

DE = EF.

b. Vì (chứng minh trên)

Tam giác DIF cân tại I.

Ví dụ 8

Cho tam giác ABC cân tại A có

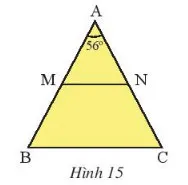
a. Tính .

b. Gọi M, N lần lượt là trung điểm của AB, AC. Chứng minh tam giác AMN cân.

c. Chứng minh rằng MN // BC.

Gợi ý đáp án:

a. Vì tam giác ABC cân tại A

b. Vì M, N lần lượt là trung điểm của AB, AC nên

mà AB = AC ( vì cân)

Tam giác AMN cân tại A.

c. Xét cân tại A có:

Xét cân tại A có:

Mà 2 góc này ở vị trí đồng vị

.

6. Bài tập tam giác cân có đáp án

Bài 1: Chọn câu sai

A. Tam giác đều có ba góc bằng nhau va bằng 60°

B. Tam giác đều có ba cạnh bằng nhau.

C. Tam giác cân là tam giác đều.

D. Tam giác đều là tam giác cân.

Gợi ý

Tam giác đều là tam giác có ba cạnh bằng nhau

Trong tam giác đều, mỗi góc bằng 60°

Tam giác đều cũng là tam giác cân nhưng tam giác cân chưa chắc là tam giác đều

Chọn đáp án C.

Bài 2: Hai góc nhọn của tam giác vuông cân bằng

A. 30°

B. 45°

C. 60°

D. 90°

Mỗi góc nhọn của tam giác vuông cân bằng 45°

Chọn đáp án B.

Bài 3: Cho tam giác ABC cân tại A. Chọn phát biểu sai

Gợi ý

Do tam giác ABC cân tại A nên ∠B = ∠C

Do đó đáp án D sai

Chọn đáp án D.

Bài 4: Một tam giác cân có góc ở đỉnh là 64° thì số đo góc đáy bằng?

A. 54°

B. 58°

C. 72°

D. 90°

Gợi ý

Góc ở đỉnh là , góc ở đáy là

Áp dụng công thức số đo ở đáy là:

Chọn đáp án B.

Bài 5: Một tam giác cân có góc ở đáy bằng 70° thì góc ở đỉnh bằng bao nhiêu?

A. 64°

B. 53°

C. 70°

D. 40°

Góc ở đỉnh là góc ở đáy là

Áp dụng công thức số đo ở đỉnh là: 180° – 2.70° = 40°

Chọn đáp án D.

Bài 6: Trong các đáp án dưới đây đáp án nào sai

A. Tam giác đều có ba góc bằng nhau và mỗi góc bằng 60°

B. Tam giác đều là tam giác có ba cạnh bằng nhau

C. Tam giác cân là tam giác đều

D. Tam giác đều là tam giác cân đặc biệt.

Đáp án đúng: C. Tam giác cân là tam giác đều- đây là một khẳng định sai

Giải thích:

– Tam giác đều là tam giác có ba cạnh bằng nhau và ba góc đều bằng nhau, mỗi góc có độ lớn 60° (π/3 radian). Tam giác cân là tam giác có hai cạnh bằng nhau và hai góc tại hai đỉnh cân có độ lớn bằng nhau.

– Tam giác đều có thể coi là một trường hợp đặc biệt của tam giác cân, vì tam giác đều không chỉ có hai cạnh bằng nhau mà còn có ba cạnh bằng nhau. Nhưng tam giác cân không nhất thiết phải có ba cạnh bằng nhau, nó chỉ cần có hai cạnh bằng nhau.

Vậy, đáp án C là sai. Tam giác cân không phải là tam giác đều, mà chỉ là một loại tam giác có hai cạnh bằng nhau.

Bài 7: Dựa vào đặc điểm của tam giác cân, hãy chọn đáp án đúng

Tam giác cân là một tam giác mang đặc điểm là:

A. có hai đường cao trong tam giác bằng nhau

B. hai đường trung tuyến có độ dài bằng nhau

C. có hai cạnh bên bằng độ dài với nhau

D. có hai tia phân giác trong cùng số đo

Đáp án đúng: C. Tam giác cân là một tam giác có hai cạnh bên bằng độ dài với nhau

Giải thích:

Tam giác cân là tam giác có hai cạnh bằng nhau và hai góc ở đỉnh cân bằng nhau. Điều này đồng nghĩa với việc tam giác cân có hai cạnh bên (hai cạnh có đỉnh chung) có độ dài bằng nhau.

Các đáp án khác không đúng với định nghĩa của tam giác cân:

A. Hai đường cao của tam giác cân không nhất thiết phải bằng nhau. Đường cao là đoạn thẳng nối một đỉnh của tam giác với đối diện với cạnh đối diện đỉnh đó.

B. Hai đường trung tuyến của tam giác cân không nhất thiết phải bằng nhau. Đường trung tuyến là đoạn thẳng nối một đỉnh của tam giác với trung điểm của cạnh đối diện đỉnh đó.

D. Hai tia phân giác trong của tam giác cân không nhất thiết phải bằng nhau. Tia phân giác trong là tia xuất phát từ một đỉnh của tam giác và chia đôi góc tại đỉnh đó.

Bài 8 Chọn đáp án đúng trong các đáp án sau, biết Tam giác ABC cân tại A, biết rằng số đo góc B là 50^o , vậy số đo các góc còn lại của tam giác ABC đã cho là:

A. Góc A = 50^o, Góc C = 80^o

B. Góc A = 80^o, Góc C = 50^o

C. Góc A = 40^o, Góc C = 90^o

D. Góc A = 90^o, Góc C = 40^o

Đáp án đúng: B- Số đo các góc còn lại trong tam giá cân ABC là Góc A = 80^o và Góc C = 50^o

Giải thích:

Tam giác ABC là tam giác cân tại A, tức là AB = AC và góc tại đỉnh A có độ lớn là 50^o (theo điều kiện trong câu hỏi).

Vì ABC là tam giác cân nên góc B và góc C (góc ở hai đỉnh chân) có độ lớn bằng nhau.

Vì tổng ba góc trong tam giác là 180^o, ta có:

Góc B + Góc A + Góc C = 180^o

50° + Góc A + Góc C = 180^o

Do đó: Góc A + Góc C = 180^o – 50^o = 130^o

Từ đó suy ra, số đo các góc sẽ là: góc B = góc C = 50^o, góc A = 130^o – góc C = 80^o

7. Một số bài tập tự luyện

A. TRẮC NGHIỆM

Câu 1: Cho tam giác cân ABC cân tại A có = 50 . Tính số đo của và .

A. = = 50

B. = = 60

C. = = 65

D. = = 70

Câu 2: Cho tam giác MNP cân tại M có = 70 . Tính số đo của . Câu nào sau đây đúng:

A.40

B.48

C.52

D.60

Câu 3: CHo tam giác ABC cân tại A. lấy điểm M thuộc canh AB và N thuốc cjanh AC sao cho AM=AN. Gọi I là giao điểm của BN và CM. Câu nào sau đây sai:

A.BM=CN

B.BN=CM

C. Δ A M N là tam giác cân

D.A,B đúng, C sai

Câu 4: Với đề bài câu trên, tam giác BIC là tam giác gì?

A.Tam giác vuông

B.Tam giác cân

C.Tam giác vuông cân

D.A,B,C đều sai

Câu 5: Cho tam giác ABC, về phía ngoài Δ A B C vẽ hai tam giác đều ABH và ACK. So sánh đoạn thẳng BK và CH

A.BK=CH

B.BK

C.BK>CH

Câu 6: Một tam giác cân có góc ở đỉnh là 64° thì số đo góc đáy bằng?

A. 54°

B. 58°

C. 72°

D. 90°

Câu 7: Một tam giác cân có góc ở đáy bằng 70° thì góc ở đỉnh bằng bao nhiêu?

A. 64°

B. 53°

C. 70°

D. 40°

B. Tự luận 

Bài 1. Cho ABC cân tại A có . Tính số đo các góc B và C.

Bài 2. Cho  ABC  cân tại A có . Tính số đo các góc B và C.

Bài 3. Cho cân tại P có . Tính số đo các góc

Bài 4. Cho ABC vuông cân tại A có . Tính số đo các góc B và C.

Bài 5. Cho ABC cân tại A có Tính số đo các góc A và C.

Bài 6. Cho cân tai . Tính số đo các góc M và F

Bài 7. Cho cân tai Q có . Tính số đo các góc P và Q

Bài 8. Cho ABC  vuông cân tại A. Trên tia đối của tia B C lấy điểm D sao cho B D=A B. Tính số đo góc ADB.

Bài 9. Cho cân tại A có . Hai tia phân giác góc B và C cắt nhau tại I. Tính Bài số đo góc BIC.

Bài 10. Cho ABC  cân tại A có . Hai tia phân giác góc B và C cắt nhau tai I, biết số đo . Tính số đo góc A.

Bài 11. Cho tam giác ABC  cân tại A có . Tia phân giác góc B cắt AC tai I. Tính số đo góc BIC

Bài 12: Cho góc nhọn xOy. Điểm H nằm trên tia phân giác của góc xOy. Từ H dựng các đường vuông góc xuống hai cạnh Ox và Oy (A thuộc Ox và B thuộc Oy).

a) Chứng minh tamgiác HAB là tamgiác cân

b)Dlà hình chiếu của điểm A trên Oy, C là giao điểm của AD với O. Chứng minh BC ⊥ Ox.

c) Khi góc xOy bằng 60⁰, chứng minh OA = 2O

Bài 13: Cho ∆ABC cân tại A và hai đường trung tuyến BM, CN cắt nhau tại K.

a) Chứng minh rBNC = rCMB

b) Chứng minh ∆BKCcân tại K

c) Chứngminh BC

Bài 14: Cho ∆ ABC vuông tại A có BD là phân giác, kẻ DE ⊥ BC ( E∈BC ). Gọi F là giao điểm của AB và DE. Chứng minh rằng

a) BD là trung trực của AE

b) DF = DC

c) AD