Download.vn Học tập Lớp 11 Toán 11
Bạn đang đọc: Các dạng toán đường thẳng và mặt phẳng trong không gian, quan hệ song song
Các dạng toán đường thẳng và mặt phẳng trong không gian, quan hệ song song Tài liệu ôn tập chương II lớp 11 môn Toán
Giới thiệu Tải về Bình luận
- 6
Mua tài khoản Download Pro để trải nghiệm website Download.vn KHÔNG quảng cáo & tải File cực nhanh chỉ từ 79.000đ. Tìm hiểu thêm Mua ngay
Các dạng toán đường thẳng và mặt phẳng trong không gian, quan hệ song song là tài liệu cực kì hữu ích mà Download.vn muốn giới thiệu đến các bạn học sinh lớp 11 cùng tham khảo.
Tài liệu bao gồm 32 trang tổng hợp các dạng bài tập chương II lớp 11 môn Toán. Tài liệu giúp các bạn học sinh lớp 11 có thêm nhiều tài liệu tham khảo củng cố kiến thức chương II để đạt được kết quả cao trong các bài kiểm tra, bài thi sắp tới. Mời các bạn cùng tham khảo và tải tài liệu tại đây.
Các dạng toán đường thẳng và mặt phẳng trong không gian, quan hệ song song
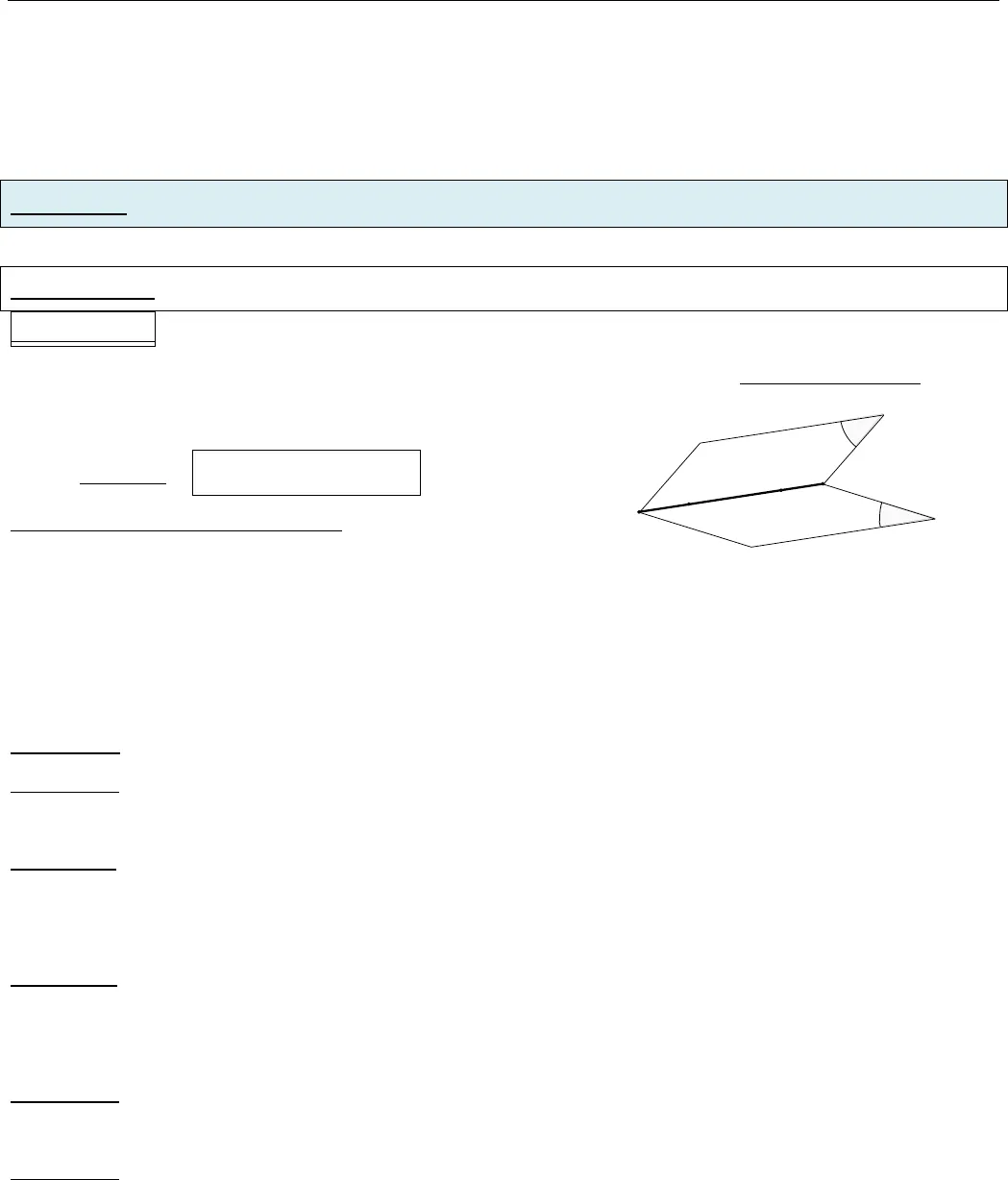 Chuyên đề HÌNH HỌC KHÔNG GIAN Hình học 11 CB Sưu tầm và biên tập: LÊ BÁ BẢO…0935.785.115…. CLB Giáo viên trẻ TP Huế -1- CHƢƠNG II. ĐƢỜNG THẲNG VÀ MẶT PHẲNG TRONG KHÔNG GIAN. QUAN HỆ SONG SONGChủ đề 1: ĐẠI CƢƠNG VỀ ĐƢỜNG THẲNG VÀ MẶT PHẲNG Dạng toán 1: XÁC ĐỊNH GIAO TUYẾN CỦA HAI MẶT PHẲNG Phương pháp: Muốn tìm giao tuyến của hai mặt phẳng αvà βta đi tìm hai điểm chung I; J của mp αvà mp β.Kí hiệu: mp mp IJαβKhi tìm điểm chung ta chú ý: Cách gọi tên hai mặt phẳng để phát hiện điểm chung. Md và d mp α M α a b M Pa ;bαα M là điểm chung của (P) và α.BÀI TẬP:Bài tập 1: Cho tứ diện ABCD với E là trung điểm của AB. Hãy xác định giao tuyến của mặt phẳng (ECD) với các mặt phẳng (ABC), (ABD), (BCD), (ACD). Bài tập 2: Cho tứ diện SABC và một điểm I trên đoạn SA, d là đường thẳng trong (ABC) cắt AB, BC tại J và K. Tìm giao tuyến của mặt phẳng (I ;d) với các mặt phẳng sau: (SAB),(SAC), (SBC).Bài tập 3: Cho tứ giác lồi ABCD với hai cặp cạnh đối không song song và điểm S không nằm trong mặt phẳng chứa tứ giác. Tìm giao tuyến của các mặt phẳng: a) (SAC) và (SBD). b) (SAB) và (SCD). c) (SAD) và (SBC). Bài tập 4: Cho hình chóp S.ABCDE. Hãy xác định giao tuyến của mặt phẳng (SAC) với các mặt phẳng (SAD), (SCE). Bài tập 5: Cho hình chóp S.ABCD có đáy ABCD là một tứ giác lồi, M là điểm trên cạnh CD. Tìm giao tuyến của các cặp mặt phẳng: a) (SAM) và (SBD). b) (SBM) và (SAC).JI
Chuyên đề HÌNH HỌC KHÔNG GIAN Hình học 11 CB Sưu tầm và biên tập: LÊ BÁ BẢO…0935.785.115…. CLB Giáo viên trẻ TP Huế -1- CHƢƠNG II. ĐƢỜNG THẲNG VÀ MẶT PHẲNG TRONG KHÔNG GIAN. QUAN HỆ SONG SONGChủ đề 1: ĐẠI CƢƠNG VỀ ĐƢỜNG THẲNG VÀ MẶT PHẲNG Dạng toán 1: XÁC ĐỊNH GIAO TUYẾN CỦA HAI MẶT PHẲNG Phương pháp: Muốn tìm giao tuyến của hai mặt phẳng αvà βta đi tìm hai điểm chung I; J của mp αvà mp β.Kí hiệu: mp mp IJαβKhi tìm điểm chung ta chú ý: Cách gọi tên hai mặt phẳng để phát hiện điểm chung. Md và d mp α M α a b M Pa ;bαα M là điểm chung của (P) và α.BÀI TẬP:Bài tập 1: Cho tứ diện ABCD với E là trung điểm của AB. Hãy xác định giao tuyến của mặt phẳng (ECD) với các mặt phẳng (ABC), (ABD), (BCD), (ACD). Bài tập 2: Cho tứ diện SABC và một điểm I trên đoạn SA, d là đường thẳng trong (ABC) cắt AB, BC tại J và K. Tìm giao tuyến của mặt phẳng (I ;d) với các mặt phẳng sau: (SAB),(SAC), (SBC).Bài tập 3: Cho tứ giác lồi ABCD với hai cặp cạnh đối không song song và điểm S không nằm trong mặt phẳng chứa tứ giác. Tìm giao tuyến của các mặt phẳng: a) (SAC) và (SBD). b) (SAB) và (SCD). c) (SAD) và (SBC). Bài tập 4: Cho hình chóp S.ABCDE. Hãy xác định giao tuyến của mặt phẳng (SAC) với các mặt phẳng (SAD), (SCE). Bài tập 5: Cho hình chóp S.ABCD có đáy ABCD là một tứ giác lồi, M là điểm trên cạnh CD. Tìm giao tuyến của các cặp mặt phẳng: a) (SAM) và (SBD). b) (SBM) và (SAC).JI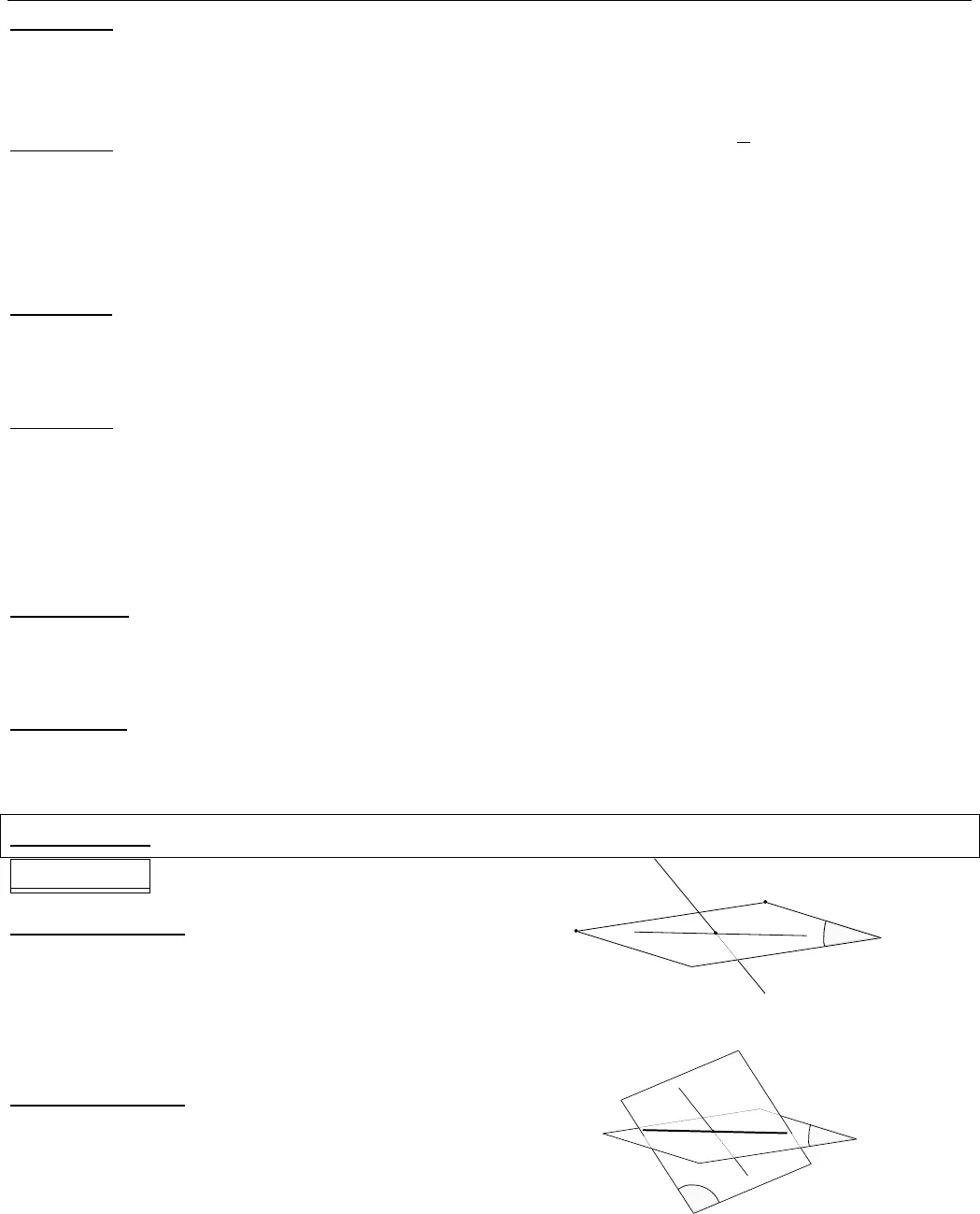 Chuyên đề HÌNH HỌC KHÔNG GIAN Hình học 11 CB Sưu tầm và biên tập: LÊ BÁ BẢO…0935.785.115…. CLB Giáo viên trẻ TP Huế -2- Bài tập 6: Cho tứ diện ABCD, M là điểm thuộc miền trong tam giác ABC, N là điểm thuộc miền trong tam giác ACD. Tìm giao tuyến của các cặp mặt phẳng: a) (AMN) và (BCD) b) (CMN) và (ABD).Bài tập 7: Cho tứ diện ABCD. Điểm M nằm trên AB sao cho AM = 41MB, N nằm trên AC sao cho AN = 3NC, điểm I nằm trong mặt phẳng (BCD). Tìm giao tuyến của các cặp mặt phẳng: a) (MNI) và (BCD). b) (MNI) và (ABD). c) (MNI) và (ACD).Bài tập 8: Cho tứ diện ABCD. Gọi I, J lần lượt là trung điểm của AD và BC. a) Tìm giao tuyến của mặt phẳng (IBC) và mặt phẳng (JAD). b) M là điểm trên AB và N là điểm trên AC. Tìm giao tuyến của (IBC) và (DMN)Bài tập 8: Cho tứ diện SABC. Gọi G là trọng tâm của tam giác ABC và M, N, P lần lượt là trung điểm của các cạnh AB, BC, CA. Điểm E, F lần lượt là 2 điểm trên SB và SC. Xác định giao tuyến của các cặp mặt phẳng sau: a) (SAN) và (SBP). b) (SCM) và (SBP). c) (AEF) và (ABC). d) (AEF) và (ASG). Bài tập 10: Cho hình chóp S.ABCD có đáy là hình thang với hai đáy là AB và CD. Tìm giao tuyến của: a) (SAD) và (SBC). b) (SAC) và (SBD)Bài tập 11: Hình chóp S.ABCD có đáy ABCD là hình thang hai đáy là AD và BC. Gọi M, N là trung điểm AB, CD và G là trọng tâm SAD. Tìm giao tuyến của các cặp mặt phẳng: a) (GMN) và (SAC). b) (GMN) và (SBC).Dạng toán 2: TÌM GIAO ĐIỂM CỦA ĐƢỜNG THẲNG VÀ MẶT PHẲNG Phương pháp: Giả sử phải tìm giao điểm mpd?αPhƣơng pháp 1: Bƣớc 1: Tìm a α Bƣớc 2: Chỉ ra được a, d nằm trong cùng mặt phẳng và chúng cắt nhau tại M: d α= M (hình vẽ)Phƣơng pháp 2: Bƣớc 1: Tìm βchứa d thích hợp. Bƣớc 2: Tìm giao tuyếnacủa αvà βBƣớc 3: Xác định giao điểm của a và d.adMadM
Chuyên đề HÌNH HỌC KHÔNG GIAN Hình học 11 CB Sưu tầm và biên tập: LÊ BÁ BẢO…0935.785.115…. CLB Giáo viên trẻ TP Huế -2- Bài tập 6: Cho tứ diện ABCD, M là điểm thuộc miền trong tam giác ABC, N là điểm thuộc miền trong tam giác ACD. Tìm giao tuyến của các cặp mặt phẳng: a) (AMN) và (BCD) b) (CMN) và (ABD).Bài tập 7: Cho tứ diện ABCD. Điểm M nằm trên AB sao cho AM = 41MB, N nằm trên AC sao cho AN = 3NC, điểm I nằm trong mặt phẳng (BCD). Tìm giao tuyến của các cặp mặt phẳng: a) (MNI) và (BCD). b) (MNI) và (ABD). c) (MNI) và (ACD).Bài tập 8: Cho tứ diện ABCD. Gọi I, J lần lượt là trung điểm của AD và BC. a) Tìm giao tuyến của mặt phẳng (IBC) và mặt phẳng (JAD). b) M là điểm trên AB và N là điểm trên AC. Tìm giao tuyến của (IBC) và (DMN)Bài tập 8: Cho tứ diện SABC. Gọi G là trọng tâm của tam giác ABC và M, N, P lần lượt là trung điểm của các cạnh AB, BC, CA. Điểm E, F lần lượt là 2 điểm trên SB và SC. Xác định giao tuyến của các cặp mặt phẳng sau: a) (SAN) và (SBP). b) (SCM) và (SBP). c) (AEF) và (ABC). d) (AEF) và (ASG). Bài tập 10: Cho hình chóp S.ABCD có đáy là hình thang với hai đáy là AB và CD. Tìm giao tuyến của: a) (SAD) và (SBC). b) (SAC) và (SBD)Bài tập 11: Hình chóp S.ABCD có đáy ABCD là hình thang hai đáy là AD và BC. Gọi M, N là trung điểm AB, CD và G là trọng tâm SAD. Tìm giao tuyến của các cặp mặt phẳng: a) (GMN) và (SAC). b) (GMN) và (SBC).Dạng toán 2: TÌM GIAO ĐIỂM CỦA ĐƢỜNG THẲNG VÀ MẶT PHẲNG Phương pháp: Giả sử phải tìm giao điểm mpd?αPhƣơng pháp 1: Bƣớc 1: Tìm a α Bƣớc 2: Chỉ ra được a, d nằm trong cùng mặt phẳng và chúng cắt nhau tại M: d α= M (hình vẽ)Phƣơng pháp 2: Bƣớc 1: Tìm βchứa d thích hợp. Bƣớc 2: Tìm giao tuyếnacủa αvà βBƣớc 3: Xác định giao điểm của a và d.adMadM Chuyên đề HÌNH HỌC KHÔNG GIAN Hình học 11 CB Sưu tầm và biên tập: LÊ BÁ BẢO…0935.785.115…. CLB Giáo viên trẻ TP Huế -3- BÀI TẬP:Bài tập 1: Cho tứ diện SABC với M, N lần lượt là các điểm nằm trong (SAB) và (SBC). Xác định giao điểm của MN và mặt phẳng (ABC). Bài tập 2: Cho tứ diện ABCD. Gọi M là trung điểm AB, N và P lần lượt là các điểm nằm trên AC, AD sao cho AN : AC = 3 : 4, AP : AD = 2 : 3. Gọi Q là trung điểm NP . Tìm giaođiểm: a) MN với (BCD). b) BD với (MNP). c) MQ với (BCD).Bài tập 3: Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của AC và BC. Trên đoạn BD lấy P sao cho BP= 2PD. Tìm giao điểm của: a) CD với (MNP). b) AD với (MNP).Bài tập 4: Cho hình chóp S.ABC, O là điểm thuộc miền trong tam giác ABC. Điểm D và E là các điểm nằm trên cạnh SB, SC. Tìm giao điểm của: a) DE với (SAO). b) SO với (ADE).Bài tập 5: Cho tứ diện SABC. Gọi I, H lần lượt là trung điểm SA và AB. Trên đoạn SC lấy điểm K sao cho CK = 3KS. a) Tìm giao điểm của đường thẳng BC với (IHK). b) Gọi M là trung điểm HI. Tìm giao điểm của đường thẳng KM với (ABC).Bài tập 6: Cho hình chóp S.ABCD đáy là hình thang ABCD đáy lớn AB. Gọi I, J, K là ba điểm trên cạnh SA, SB, SC. a) Tìm giao điểm IK và (SBD). b) Giao điểm (IJK) và SD; SC. Bài tập 7: Gọi I, J lần lượt là hai điểm nằm trên mp(ABC) và mp(ABD) của tứ diện ABCD. M là điểm tuỳ ý trên cạnh CD. Tìm giao điểm IJ và mặt phẳng (AMB). Bài tập 8: Hình chóp S.ABCD đáy là hình bình hành với M là trung điểm SD. a) Tìm giao điểm I của BM và (SAC). Chứng minh: BI = 2IM. b) Tìm giao điểm J của của SA và (BCM). Chứng minh: J là trung điểm SA.c) N là điểm tuỳ ý trên cạnh BC. Tìm giao điểm của MN với (SAC). Bài tập 9: Cho tứ diện ABCD có các điểm M và N lần lượt là trung điểm của AC và BC. Lấy điểm K thuộc đoạn BD (K không là trung điểm BD). Tìm giao điểm của đường thẳngAD và mặt phẳng (MNK). Bài tập 10: Cho hình chóp S.ABCD. Lấy M, N và P lần lượt là các điểm trên các đoạn SA, AB và BC sao cho chúng không trùng với trung điểm của các đoạn thẳng ấy. Tìm giao điểm (nếu có) của mặt phẳng (MNP) và các cạnh của hình chóp. Bài tập 11: Cho hình chóp S.ABCD. Gọi M, N lần lượt là các điểm thuộc các cạnh SC và BC. Tìm giao điểm của đường thẳng SD và mặt phẳng (AMN).
Chuyên đề HÌNH HỌC KHÔNG GIAN Hình học 11 CB Sưu tầm và biên tập: LÊ BÁ BẢO…0935.785.115…. CLB Giáo viên trẻ TP Huế -3- BÀI TẬP:Bài tập 1: Cho tứ diện SABC với M, N lần lượt là các điểm nằm trong (SAB) và (SBC). Xác định giao điểm của MN và mặt phẳng (ABC). Bài tập 2: Cho tứ diện ABCD. Gọi M là trung điểm AB, N và P lần lượt là các điểm nằm trên AC, AD sao cho AN : AC = 3 : 4, AP : AD = 2 : 3. Gọi Q là trung điểm NP . Tìm giaođiểm: a) MN với (BCD). b) BD với (MNP). c) MQ với (BCD).Bài tập 3: Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của AC và BC. Trên đoạn BD lấy P sao cho BP= 2PD. Tìm giao điểm của: a) CD với (MNP). b) AD với (MNP).Bài tập 4: Cho hình chóp S.ABC, O là điểm thuộc miền trong tam giác ABC. Điểm D và E là các điểm nằm trên cạnh SB, SC. Tìm giao điểm của: a) DE với (SAO). b) SO với (ADE).Bài tập 5: Cho tứ diện SABC. Gọi I, H lần lượt là trung điểm SA và AB. Trên đoạn SC lấy điểm K sao cho CK = 3KS. a) Tìm giao điểm của đường thẳng BC với (IHK). b) Gọi M là trung điểm HI. Tìm giao điểm của đường thẳng KM với (ABC).Bài tập 6: Cho hình chóp S.ABCD đáy là hình thang ABCD đáy lớn AB. Gọi I, J, K là ba điểm trên cạnh SA, SB, SC. a) Tìm giao điểm IK và (SBD). b) Giao điểm (IJK) và SD; SC. Bài tập 7: Gọi I, J lần lượt là hai điểm nằm trên mp(ABC) và mp(ABD) của tứ diện ABCD. M là điểm tuỳ ý trên cạnh CD. Tìm giao điểm IJ và mặt phẳng (AMB). Bài tập 8: Hình chóp S.ABCD đáy là hình bình hành với M là trung điểm SD. a) Tìm giao điểm I của BM và (SAC). Chứng minh: BI = 2IM. b) Tìm giao điểm J của của SA và (BCM). Chứng minh: J là trung điểm SA.c) N là điểm tuỳ ý trên cạnh BC. Tìm giao điểm của MN với (SAC). Bài tập 9: Cho tứ diện ABCD có các điểm M và N lần lượt là trung điểm của AC và BC. Lấy điểm K thuộc đoạn BD (K không là trung điểm BD). Tìm giao điểm của đường thẳngAD và mặt phẳng (MNK). Bài tập 10: Cho hình chóp S.ABCD. Lấy M, N và P lần lượt là các điểm trên các đoạn SA, AB và BC sao cho chúng không trùng với trung điểm của các đoạn thẳng ấy. Tìm giao điểm (nếu có) của mặt phẳng (MNP) và các cạnh của hình chóp. Bài tập 11: Cho hình chóp S.ABCD. Gọi M, N lần lượt là các điểm thuộc các cạnh SC và BC. Tìm giao điểm của đường thẳng SD và mặt phẳng (AMN). 
