Download.vn Học tập Lớp 12
Bạn đang đọc: Các dạng toán đường tiệm cận của đồ thị hàm số
Các dạng toán đường tiệm cận của đồ thị hàm số Tài liệu ôn tập môn Toán lớp 12
Giới thiệu Tải về Bình luận
- 16
Mua tài khoản Download Pro để trải nghiệm website Download.vn KHÔNG quảng cáo & tải File cực nhanh chỉ từ 79.000đ. Tìm hiểu thêm Mua ngay
Với mong muốn đem đến cho các bạn học sinh lớp 12 có thêm nhiều tài liệu học tập, Download.vn xin giới thiệu Các dạng toán đường tiệm cận của đồ thị hàm số.
Đây là tài liệu hữu ích, gồm 26 trang hướng dẫn phương pháp giải và các bài toán có lời giải chi tiết dạng toán đường tiệm cận của đồ thị hàm số, ôn luyện kỳ thi THPT Quốc gia 2020 môn Toán. Nội dung chi tiết mời các bạn cùng tham khảo và tải tài liệu tại đây.
Các dạng toán đường tiệm cận của đồ thị hàm số
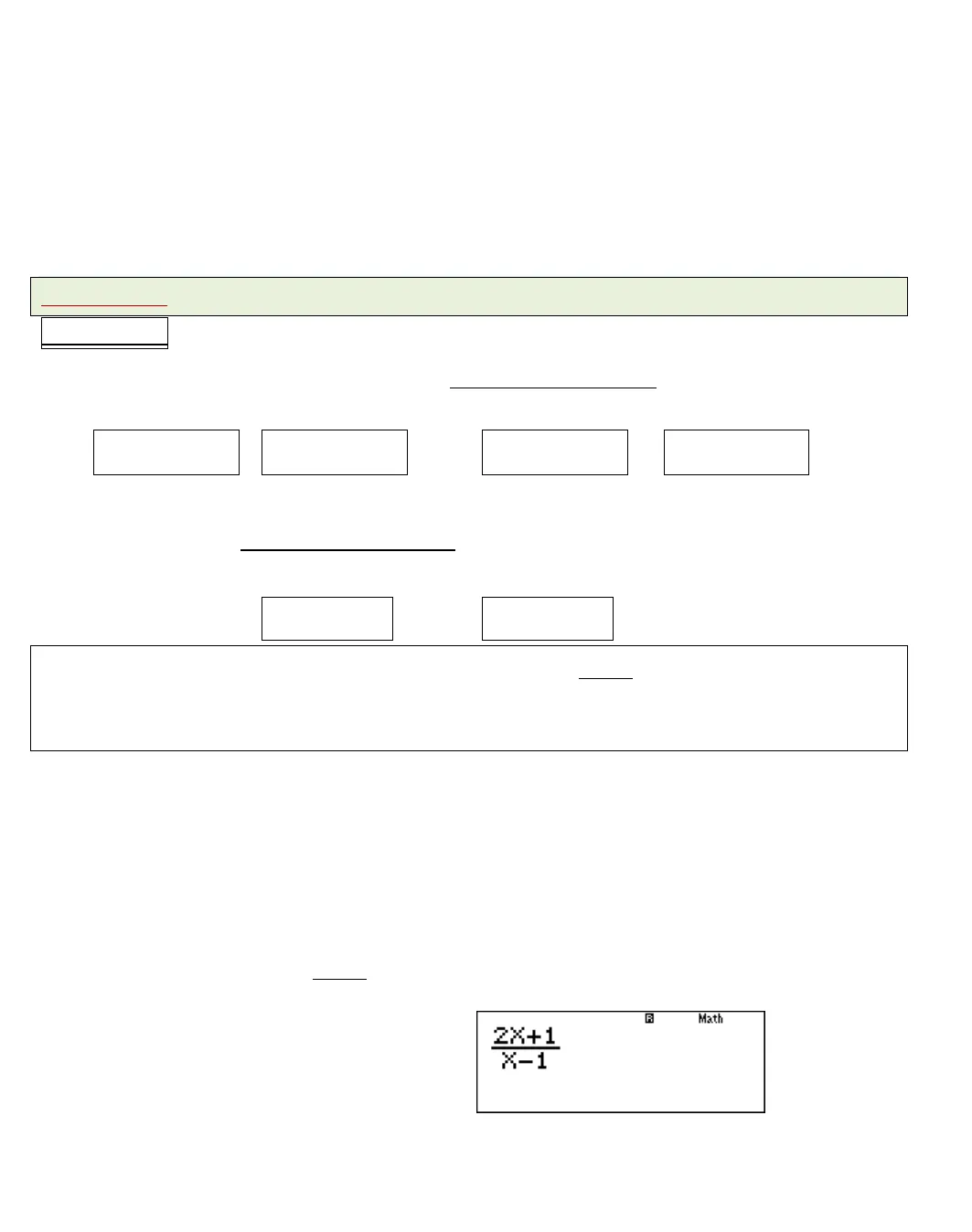 […Các chuyên đề Trắc nghiệm Toán THPT…] Giải tích 12 CB Giáo viên: LÊ BÁ BẢO…0935.785.115… CLB Giáo viên trẻ TP Huế ……………….1 Page: CLB GIÁO VIÊN TRẺ TP HUẾ CHUY£N §Ò TR¾C NGHIÖMM«n: To¸n 12 CBChñ ®Ò:§-êng tiÖm cËnDành tặng cho các em học sinh đang sợ Toán, yếu Toán và đang loay hoay về Toán! Cố lên các em! Giáo viên: LÊ BÁ BẢO Trường THPT Đặng Huy Trứ, Huế SĐT: 0935.785.115 Địa chỉ: 116/04 Nguyễn Lộ Trạch, TP Huế Dạng toán 1:T×m ®-êng tiÖm cËn cña ®å thÞ hµm sè.Phương pháp:Cho hàm số .y f x +) Đường thẳngxađược gọi là đường tiệm cận đứng (gọi tắt là tiệm cận đứng)của đồ thị hàm số khi một trong các điều kiện sau được thỏa mãn: limxay limxay limxay limxay +) Hàm số fxxác định trên khoảngK“có chứa kí hiệu hoặc . Đường thẳng ybđược gọi là đường tiệm cận ngang (gọi tắt là tiệm cận ngang) của đồ thị hàm số khimột trong các điều kiện sau được thỏa mãn: limxyb limxyb Câu 1. Tìm các đường tiệm cận của đồ thị hàm số 21.1xyx A.1; 2.xx B.1; 2.yx C.1; 2.xy D.1; 2.xx Lời giải: +) Ta có:1lim 1xyx là tiệm cận đứng của đồ thị hàm số. +) Ta có:lim 2 2xyy là tiệm cận ngang của đồ thị hàm số. Chọn đáp án C. Sử dụng máy tính cầm tay:Nhập biểu thức hàm số 211xyxvào máy tính:a2Q)+1RQ)p1 +) Tìm đường tiệm cận đứng của đồ thị hàm số: Nghiệm của mẫu thức 1:x Nhập 0,99999999x
[…Các chuyên đề Trắc nghiệm Toán THPT…] Giải tích 12 CB Giáo viên: LÊ BÁ BẢO…0935.785.115… CLB Giáo viên trẻ TP Huế ……………….1 Page: CLB GIÁO VIÊN TRẺ TP HUẾ CHUY£N §Ò TR¾C NGHIÖMM«n: To¸n 12 CBChñ ®Ò:§-êng tiÖm cËnDành tặng cho các em học sinh đang sợ Toán, yếu Toán và đang loay hoay về Toán! Cố lên các em! Giáo viên: LÊ BÁ BẢO Trường THPT Đặng Huy Trứ, Huế SĐT: 0935.785.115 Địa chỉ: 116/04 Nguyễn Lộ Trạch, TP Huế Dạng toán 1:T×m ®-êng tiÖm cËn cña ®å thÞ hµm sè.Phương pháp:Cho hàm số .y f x +) Đường thẳngxađược gọi là đường tiệm cận đứng (gọi tắt là tiệm cận đứng)của đồ thị hàm số khi một trong các điều kiện sau được thỏa mãn: limxay limxay limxay limxay +) Hàm số fxxác định trên khoảngK“có chứa kí hiệu hoặc . Đường thẳng ybđược gọi là đường tiệm cận ngang (gọi tắt là tiệm cận ngang) của đồ thị hàm số khimột trong các điều kiện sau được thỏa mãn: limxyb limxyb Câu 1. Tìm các đường tiệm cận của đồ thị hàm số 21.1xyx A.1; 2.xx B.1; 2.yx C.1; 2.xy D.1; 2.xx Lời giải: +) Ta có:1lim 1xyx là tiệm cận đứng của đồ thị hàm số. +) Ta có:lim 2 2xyy là tiệm cận ngang của đồ thị hàm số. Chọn đáp án C. Sử dụng máy tính cầm tay:Nhập biểu thức hàm số 211xyxvào máy tính:a2Q)+1RQ)p1 +) Tìm đường tiệm cận đứng của đồ thị hàm số: Nghiệm của mẫu thức 1:x Nhập 0,99999999x 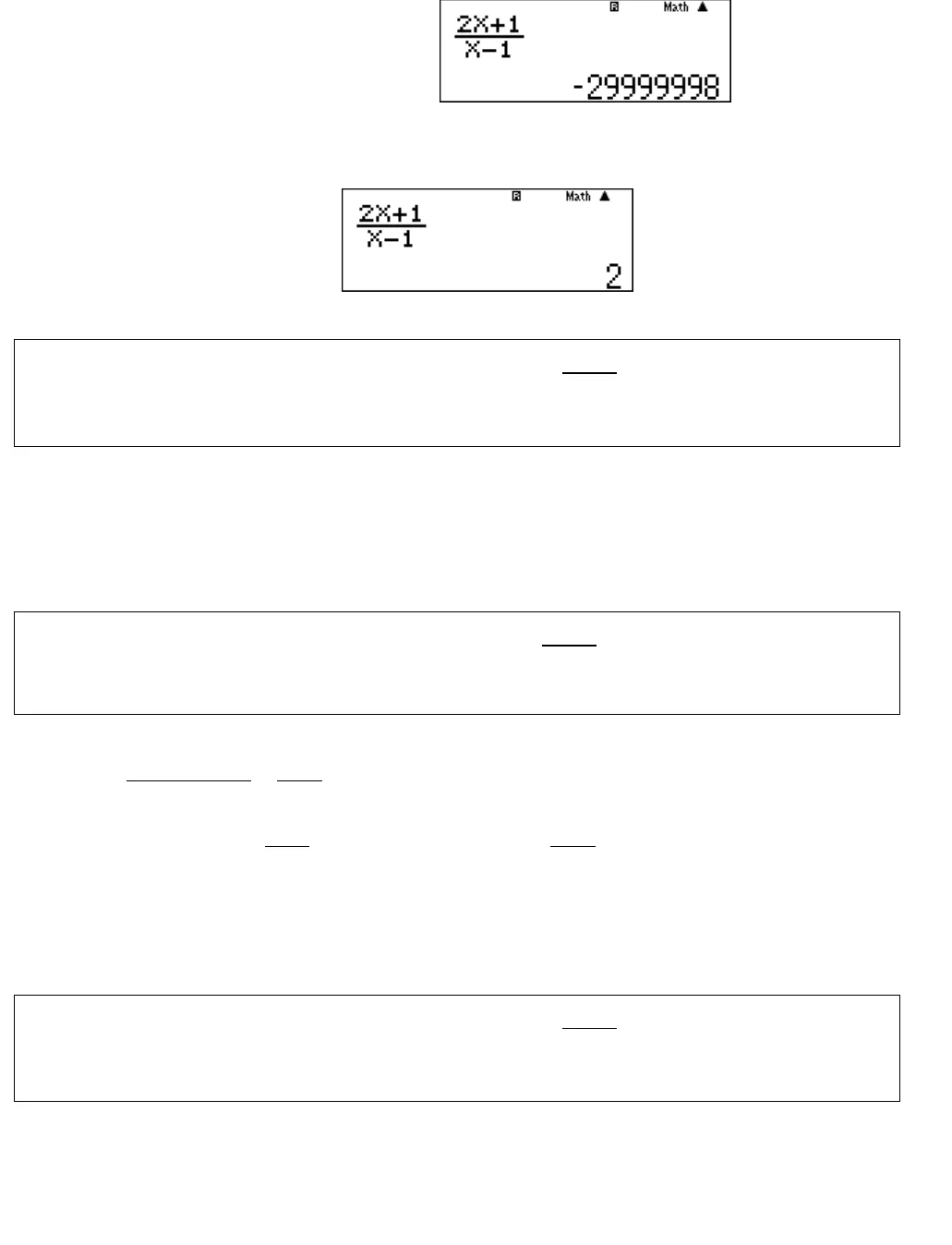 […Các chuyên đề Trắc nghiệm Toán THPT…] Giải tích 12 CB Giáo viên: LÊ BÁ BẢO…0935.785.115… CLB Giáo viên trẻ TP Huế ……………….2 r0.9999999= Kết quả:1lim 1xyx là tiệm cận đứng của đồ thị hàm số.+) Tìm đường tiệm cận ngang của đồ thị hàm số: Nhập 1010 .x r10^10)= Kết quả:lim 2 2xyy là tiệm cận ngang của đồ thị hàm số.Câu 2. Tìm các đường tiệm cận của đồ thị hàm số 31.2xyx A.2; 3.xx B.2; 3.yx C.3; 2.xy D.2; 3.xyLời giải: +) Ta có:2lim 2xyx là tiệm cận đứng của đồ thị hàm số. +) Ta có:lim 3 3xyy là tiệm cận ngang của đồ thị hàm số. Chọn đáp án D. Câu 3. (Đề THPT Quốc gia 2017) Đồ thị hàm số 224xyxcó mấy tiệm cận? A.0. B.3. C.1. D.2.Lời giải: Ta có: 222xyxx1; 2.2xx +) Ta có: 221lim lim2xxyx và 221lim lim 22xxyxx là đường tiệm cận đứng của đồ thị hàm số.+) Ta có:lim 0xyvà0ylà đường tiệm cận ngang của đồ thị hàm số.Chọn đáp án D. Câu 4. Tìm các đường tiệm cận của đồ thị hàm số 21.1xyx A.1; 2.xx B.1; 2.xy C.1; 2.xy D.1; 2.xy Lời giải: +) Ta có:1lim 1xyx là tiệm cận đứng của đồ thị hàm số. +) Ta có:lim 2 2xyy là tiệm cận ngang của đồ thị hàm số.
[…Các chuyên đề Trắc nghiệm Toán THPT…] Giải tích 12 CB Giáo viên: LÊ BÁ BẢO…0935.785.115… CLB Giáo viên trẻ TP Huế ……………….2 r0.9999999= Kết quả:1lim 1xyx là tiệm cận đứng của đồ thị hàm số.+) Tìm đường tiệm cận ngang của đồ thị hàm số: Nhập 1010 .x r10^10)= Kết quả:lim 2 2xyy là tiệm cận ngang của đồ thị hàm số.Câu 2. Tìm các đường tiệm cận của đồ thị hàm số 31.2xyx A.2; 3.xx B.2; 3.yx C.3; 2.xy D.2; 3.xyLời giải: +) Ta có:2lim 2xyx là tiệm cận đứng của đồ thị hàm số. +) Ta có:lim 3 3xyy là tiệm cận ngang của đồ thị hàm số. Chọn đáp án D. Câu 3. (Đề THPT Quốc gia 2017) Đồ thị hàm số 224xyxcó mấy tiệm cận? A.0. B.3. C.1. D.2.Lời giải: Ta có: 222xyxx1; 2.2xx +) Ta có: 221lim lim2xxyx và 221lim lim 22xxyxx là đường tiệm cận đứng của đồ thị hàm số.+) Ta có:lim 0xyvà0ylà đường tiệm cận ngang của đồ thị hàm số.Chọn đáp án D. Câu 4. Tìm các đường tiệm cận của đồ thị hàm số 21.1xyx A.1; 2.xx B.1; 2.xy C.1; 2.xy D.1; 2.xy Lời giải: +) Ta có:1lim 1xyx là tiệm cận đứng của đồ thị hàm số. +) Ta có:lim 2 2xyy là tiệm cận ngang của đồ thị hàm số.  […Các chuyên đề Trắc nghiệm Toán THPT…] Giải tích 12 CB Giáo viên: LÊ BÁ BẢO…0935.785.115… CLB Giáo viên trẻ TP Huế ……………….3 Chọn đáp án D. Câu 5. Tìm các đường tiệm cận của đồ thị hàm số 42.32xyx A.34;.23xy B.34;.23xx C.3; 2.2xy D.3; 2.2xyLời giải: +) Ta có:323lim2xyx là tiệm cận đứng của đồ thị hàm số. +) Ta có:lim 2 2xyy là tiệm cận ngang của đồ thị hàm số. Chọn đáp án C. Câu 6. Tìm các đường tiệm cận của đồ thị hàm số 1.xyx A.0; 1.xy B.1; 0.xx C.1; 1.xy D.0; 1.xy Lời giải: +) Ta có:0lim 0xyx là tiệm cận đứng của đồ thị hàm số. +) Ta có:lim 1 1xyy là tiệm cận ngang của đồ thị hàm số. Chọn đáp án A. Câu 7. Tiệm cận ngang của đồ thị hàm số 212xyxlà đường thẳng nào sau đây? A.2.x B.2.x C.2.y D.2.y Lời giải: Ta có:lim 2 2xyy là tiệm cận ngang của đồ thị hàm số.Chọn đáp án D. Câu 8. Tiệm cận đứng của đồ thị hàm số 252xyxlà đường thẳng nào sau đây? A.2.x B.2.x C.2.y D.2.y Lời giải: Ta có:2lim 2xyx là tiệm cận đứng của đồ thị hàm số.Chọn đáp án A. Câu 9. Tìm các đường tiệm cận của đồ thị hàm số 21.4xyx A.2; 0.xy B.2; 2.xx
[…Các chuyên đề Trắc nghiệm Toán THPT…] Giải tích 12 CB Giáo viên: LÊ BÁ BẢO…0935.785.115… CLB Giáo viên trẻ TP Huế ……………….3 Chọn đáp án D. Câu 5. Tìm các đường tiệm cận của đồ thị hàm số 42.32xyx A.34;.23xy B.34;.23xx C.3; 2.2xy D.3; 2.2xyLời giải: +) Ta có:323lim2xyx là tiệm cận đứng của đồ thị hàm số. +) Ta có:lim 2 2xyy là tiệm cận ngang của đồ thị hàm số. Chọn đáp án C. Câu 6. Tìm các đường tiệm cận của đồ thị hàm số 1.xyx A.0; 1.xy B.1; 0.xx C.1; 1.xy D.0; 1.xy Lời giải: +) Ta có:0lim 0xyx là tiệm cận đứng của đồ thị hàm số. +) Ta có:lim 1 1xyy là tiệm cận ngang của đồ thị hàm số. Chọn đáp án A. Câu 7. Tiệm cận ngang của đồ thị hàm số 212xyxlà đường thẳng nào sau đây? A.2.x B.2.x C.2.y D.2.y Lời giải: Ta có:lim 2 2xyy là tiệm cận ngang của đồ thị hàm số.Chọn đáp án D. Câu 8. Tiệm cận đứng của đồ thị hàm số 252xyxlà đường thẳng nào sau đây? A.2.x B.2.x C.2.y D.2.y Lời giải: Ta có:2lim 2xyx là tiệm cận đứng của đồ thị hàm số.Chọn đáp án A. Câu 9. Tìm các đường tiệm cận của đồ thị hàm số 21.4xyx A.2; 0.xy B.2; 2.xx 
