Download.vn Học tập Lớp 11 Toán 11

Bạn đang đọc: Tài liệu tự học hàm số lượng giác và phương trình lượng giác

Tài liệu tự học hàm số lượng giác và phương trình lượng giác Tài liệu ôn tập môn Toán lớp 11

Giới thiệu Tải về Bình luận

• 4

Mua tài khoản Download Pro để trải nghiệm website Download.vn KHÔNG quảng cáo & tải File cực nhanh chỉ từ 79.000đ. Tìm hiểu thêm Mua ngay

Download.vn xin giới thiệu đến các bạn tài liệu Tài liệu tự học hàm số lượng giác và phương trình lượng giác được chúng tôi tổng hợp và đăng tải ngay sau đây.

Tài liệu bao gồm 60 trang với nội dung được chia thành ba phần: Kiến thức cần nắm; Dạng bài tập có hướng dẫn giải và bài tập đề nghị; Phần trắc nghiệm có đáp án. Hy vọng với tài liệu này các bạn học sinh lớp 11 có thêm nhiều tài liệu học tập, củng cố kiến thức để đạt được kết quả trong các bài kiểm tra, bài thi học kì 1 sắp tới. Ngoài ra các bạn tham khảo thêm một số tài liệu như: Bài tập trắc nghiệm lượng giác vận dụng cao, Phương pháp giải phương trình lượng giác, Trắc nghiệm nâng cao hàm số lượng giác và phương trình lượng giá. Nội dung chi tiết, mời các bạn cùng tham khảo và tải tài liệu tại đây.

Tài liệu hàm số lượng giác và phương trình lượng giác

Tài liệu học tập Toán 11 GV. Lư Sĩ Pháp1Chương I. HSLG & PTLG Phần Tự LuậnCHƯƠNG I —0o0—HÀM SỐ LƯỢNG GIÁC & PHƯƠNG TRÌNH LƯỢNG GIÁC —0O0—ÔN TẬP CÔNG THỨC LƯỢNG GIÁC1. Hằng đẳng thức lượng giác cơ bản 2 2sin cos 1α α+ = sintan ; ,cos 2k kα πα α πα= ≠ + ∈ℤ coscot ; ,sink kαα α πα= ≠ ∈ℤ tan .cot 1; ,2kkπα α α= ≠ ∈ℤ 2211 tan ; ,2cosk kπα α πα+ = ≠ + ∈ℤ 2211 cot ; ,sink kα α πα+ = ≠ ∈ℤ2. Các công thức lượng giác2.1. Công thức cộng ()cos cos cos sin sinα β α β α β± = ∓  ()sin sin cos cos sinα β α β α β± = ±  ( )tan tantan1 tan tanα βα βα β±± =∓, với mọi,α βlàm cho các biểu thức có nghĩa.2.2. Công thức nhân đôi sin2 2sin cosα α α= 2 2 2 2cos2 cos sin 2cos 1 1 2sinα α α α α= − = − = − 22tantan2 ; ,2 ,21 tank kα πα α α πα= ≠ + ∈−ℤ2.3. Công thức nhân ba 3cos3 4cos 3cosα α α= −  3sin3 3sin 4sinα α α= − 2.4. Công thức hạ bậc 21 cos2cos2αα+= 21 cos2sin2αα−= 21 cos2tan1 cos2ααα−=+, vớiαlàm cho biểu thức có nghĩa.2.6. Công thức biến đổi tổng thành tích cos cos 2cos .cos2 2α β α βα β+ −+ = cos cos 2sin .sin2 2α β α βα β+ −− = − sin sin 2sin .cos2 2α β α βα β+ −+ =  sin sin 2cos .sin2 2α β α βα β+ −− =, với mọi,α βlàm cho các biểu thức có nghĩa.2.7. Công thức biến đổi tích thành tổng ( ) ( )1cos .cos cos cos2α β α β α β = + + −  ( ) ( )1sin .sin cos cos2α β α β α β = − + − −  ( ) ( )1sin .cos sin sin2α β α β α β = + + − 2.8. Công thức rút gọnTài liệu học tập Toán 11 GV. Lư Sĩ Pháp2Chương I. HSLG & PTLG Phần Tự Luận sin cos 2 sin 2 cos4 4π πα α α α   + = + = −       sin cos 2 sin 2 cos4 4π πα α α α   − = − = − +       2tan cotsin2α αα+ = , với αlàm cho biểu thức có nghĩa3. Giá trị lượng giác của các góc (cung) có liên quan đặt biệt3.1. Hai góc đối nhau ( cung đối) (αlàm cho các biểu thức có nghĩa) cos( ) cosα α− = sin( ) sinα α− = − tan( ) tanα α− = − cot( ) cotα α− = −3.2. Hai góc bù nhau( cung bù)(αlàm cho các biểu thức có nghĩa) sin( ) sinπ α α− = cos( ) cosπ α α− = − tan( ) tanπ α α− = − cot( ) cotπ α α− = −3.3. Hai góc phụ nhau ( cung phụ)(αlàm cho các biểu thức có nghĩa) sin cos2πα α − =   cos sin2πα α − =   tan cot2πα α − =   cot tan2πα α − =  3.4. Hai góc hơn kémπ(cung hơn kémπ),(αlàm cho các biểu thức có nghĩa) sin( ) sinπ α α+ = − cos( ) cosπ α α+ = − tan( ) tanπ α α+ = cot( ) cotπ α α+ =3.5. Hai góc hơn kém2π(cung hơn kém2π),(αlàm cho các biểu thức có nghĩa) sin cos2πα α + =   cos sin2πα α + = −   tan cot2πα α + = −   cot tan2πα α + = −  3.6. Cung bội. (k∈ℤ,αlàm cho các biểu thức có nghĩa) sin( 2 ) sinkα π α+ = cos( 2 ) coskα π α+ = tan( ) tankα π α+ = cot( ) cotkα π α+ =4. Bảng giá trị lượng giác các góc (cung) đặt biệtαHSLG00300 450 600 900 1200 1350 1500 180006π4π3π2π23π34π56ππsinα012223213222120cosα1322212012−22−32−- 1tanα03313||3−- 133−0cotα ||3133033−- 13−|| || : Không xác định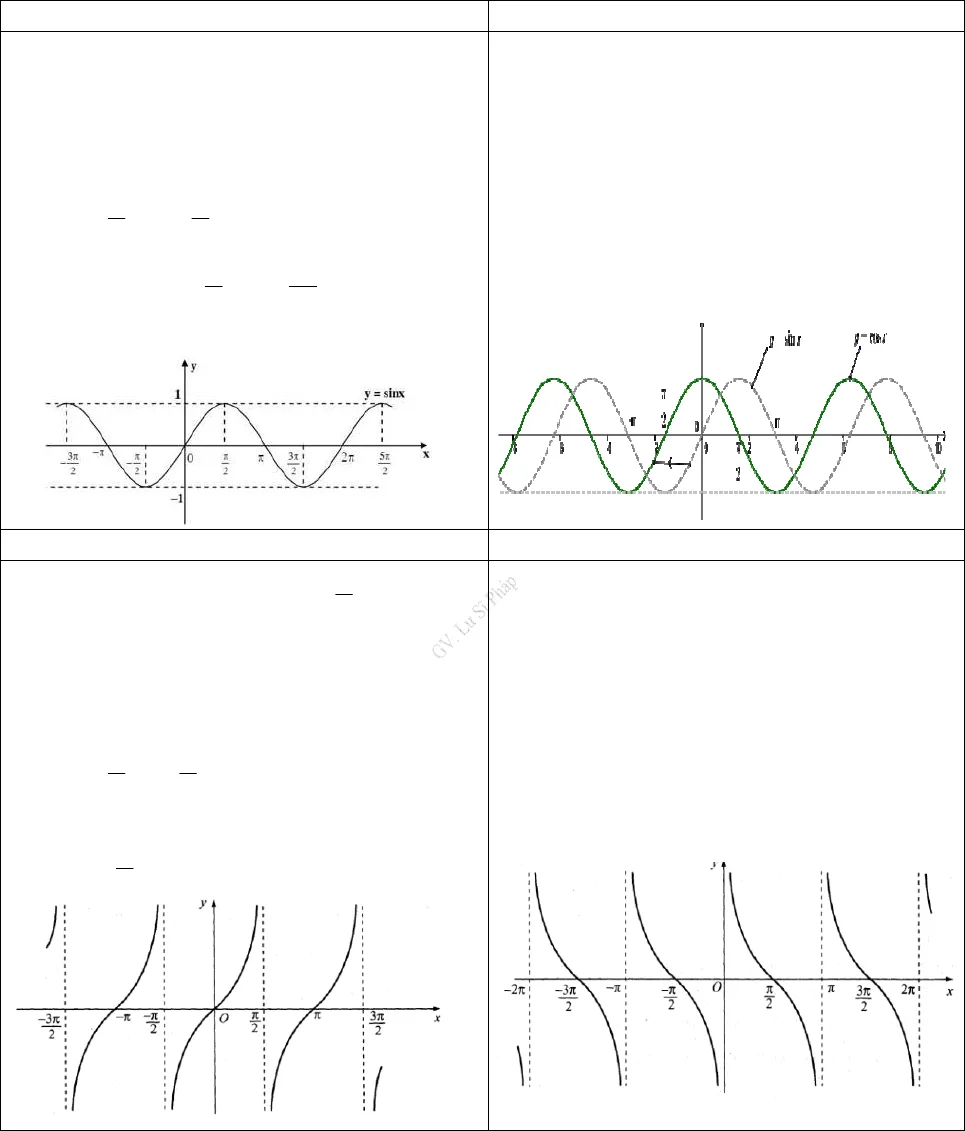Tài liệu học tập Toán 11 GV. Lư Sĩ Pháp3Chương I. HSLG & PTLG Phần Tự Luận§1. HÀM SỐ LƯỢNG GIÁCA. KIẾN THỨC CẦN NẮMHàm sốsiny x= Hàm sốcosy x=• Có tập xác định là ℝ• Có tập giá trị là 1;1 − • Là hàm số lẻ • Là hàm số tuần hoàn với chu kì 2Tπ=• Đồng biến trên mỗi khoảng 2 ; 22 2k kπ ππ π − + +  và nghịch biến trênmỗi khoảng32 ; 2 ,2 2k k kπ ππ π + + ∈  ℤ• Có đồ thị là một đường hình sin • Có tập xác định là ℝ• Có tập giá trị là 1;1 − • Là hàm số chẵn • Là hàm số tuần hoàn với chu kì 2Tπ=• Đồng biến trên mỗi khoảng ()2 ; 2k kπ π π− +và nghịch biến trên mỗikhoảng()2 ; 2 ,k k kπ π π+ ∈ℤ• Có đồ thị là một đường hình sin Hàm sốtany x= Hàm sốcoty x=• Có tập xác định là1 ,2D k kππ = + ∈  ℝ ℤ• Có tập giá trị là ℝ• Là hàm số lẻ • Là hàm số tuần hoàn với chu kì là π• Đồng biến trên mỗi khoảng ; ;2 2k k kπ ππ π − + + ∈  ℤ• Có đồ thị nhận mỗi đường thẳng ;2x k kππ= + ∈ℤlàm một đường tiệm cận• Có tập xác định là {}2 ,D k kπ= ∈ℝ ℤ• Có tập giá trị là ℝ• Là hàm số lẻ • Là hàm số tuần hoàn với chu kì là π• Nghịch biến trên mỗi khoảng (); ;k k kπ π π+ ∈ℤ• Có đồ thị nhận mỗi đường thẳng ;x k kπ= ∈ℤlàm một đường tiệm cậnB. BÀI TẬPạng 1. Tập xác định của hàm số – Hàm số xác định với một điều kiện- Hàm số xác định bởi hai hay nhiều điều kiện- Hàm sốsin ; cosy x y x= =có tập xác định là ℝ- Hàm sốtany x=xác định khi và chỉ khicos 0x≠; Hàm sốcoty x=xác định khi và chỉ khisin 0x≠D