Download.vn Học tập Lớp 12

Bạn đang đọc: Bài tập GTLN – GTNN của Số Phức

Bài tập GTLN – GTNN của Số Phức Tài liệu ôn tập môn Toán lớp 12

Giới thiệu Tải về Bình luận

• 1

Mua tài khoản Download Pro để trải nghiệm website Download.vn KHÔNG quảng cáo & tải File cực nhanh chỉ từ 79.000đ. Tìm hiểu thêm Mua ngay

Với mong muốn đem đến cho các bạn đọc có thêm nhiều tài liệu học tập môn Toán lớp 12, Download.vn giới thiệu Bài tập GTLN – GTNN của Số phức.

Bài tập giá trị lớn nhất và giá trị nhỏ nhất (viết tắt là GTLN – GTNN hoặc min – max) của biểu thức số phức là một dạng toán vận dụng cao thường gặp trong các đề thi thử THPT Quốc gia môn Toán trong những năm gần đây. Đây là dạng toán ít được đề cập đến trong sách giáo khoa Giải tích 12, do đó đã gây không ít bỡ ngỡ và khó khăn cho các bạn học sinh trong quá trình tiếp cận và tìm hướng giải quyết bài toán. Nội dung chi tiết mời các bạn cùng tham khảo và tải tại đây.

Bài tập GTLN – GTNN của Số Phức

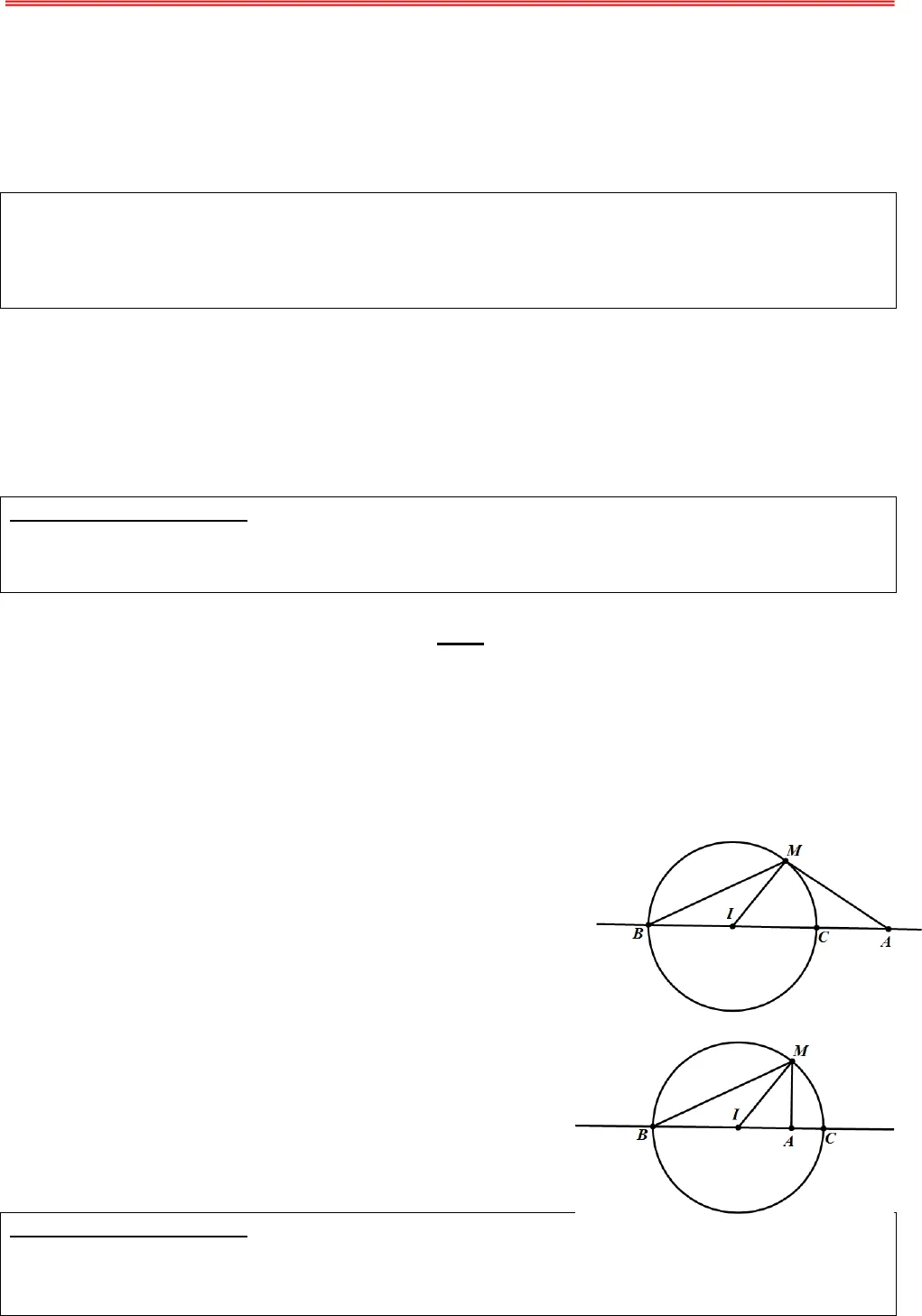https://toanmath.com/ GTLN – GTNN CỦA MÔĐUN SỐ PHỨCA. BÀI TOÁN CỰC TRỊ CỦA SỐ PHỨCI. CÁC BÀI TOÁN QUI VỀ BÀI TOÁN TÌM GIÁ TRỊ LỚN NHẤT, NHỎ NHẤT CỦA HÀMMỘT BIẾN1. PHƯƠNG PHÁPBài toán: Trong các số phứczthoả mãn điều kiện T. Tìm số phức z để biểu thức P đạt giá trị nhỏnhất, lớn nhấtTừ điều kiện T, biến đổi để tìm cách rút ẩn rồi thế vào biểu thức P để được hàm một biến. Tìm giá trị lớn nhất (hoặc nhỏ nhất) tuỳ theo yêu cầu bài toán của hàm số một biến vừa tìm được. II. CÁC BÀI TOÁN QUI VỀ BÀI TOÁN TÌM GIÁ TRỊ LỚN NHẤT, NHỎ NHẤT CỦA MỘTBIỂU THỨC HAI BIẾN MÀ CÁC BIẾN THOẢ MÃN ĐIỀU KIỆN CHO TRƯỚC.1. PHƯƠNG PHÁP:Để giải được lớp bài toán này, chúng tôi cung cấp cho học sinh các bất đẳng thức cơ bản như: Bất đẳngthức liên hệ giữa trung bình cộng và trung bình nhân, bất đẳng thức Bunhia- Cốpxki, bất đẳng thức hìnhhọc và một số bài toán công cụ sau:UBÀI TOÁN CÔNG CỤ 1:UCho đường tròn ()Tcố định có tâm I bán kính R và điểm A cố định. Điểm M di động trên đườngtròn()T. Hãy xác định vị trí điểm M sao cho AM lớn nhất, nhỏ nhất. UGiải: TH1: A thuộc đường tròn (T) Ta có: AM đạt giá trị nhỏ nhất bằng 0 khi M trùng với A AM đạt giá trị lớn nhất bằng 2R khi M là điểm đối xứng với A qua ITH2: A không thuộc đường tròn (T)Gọi B, C là giao điểm của đường thẳng qua A,I và đường tròn (T);Giả sử AB +) Nếu A nằm ngoài đường tròn (T) thì với điểm M bất kì trên (T), ta có: AM AI IM AI IB AB≥− =−=.Đẳng thức xảy ra khiMB≡AM AI IM AI IC AC≤+ =+=.Đẳng thức xảy ra khi MC≡+) Nếu A nằm trong đường tròn (T) thì với điểm M bất kì trên (T), ta có: AM IM IA IB IA AB≥ −=−=.Đẳng thức xảy ra khi MB≡AM AI IM AI IC AC≤+ =+=.Đẳng thức xảy ra khi MC≡Vậy khi M trùng với B thì AM đạt gía trị nhỏ nhất.Vậy khi M trùng với C thì AM đạt gía trị lớn nhất.UBÀI TOÁN CÔNG CỤ 2:UCho hai đường tròn 1()Tcó tâm I, bán kính RR1R; đường tròn 2()Tcó tâm J, bán kính RR2R. Tìm vị trí của điểm M trên 1()T, điểm N trên 2()Tsao cho MN đạt giá trị lớn nhất, nhỏ nhất. 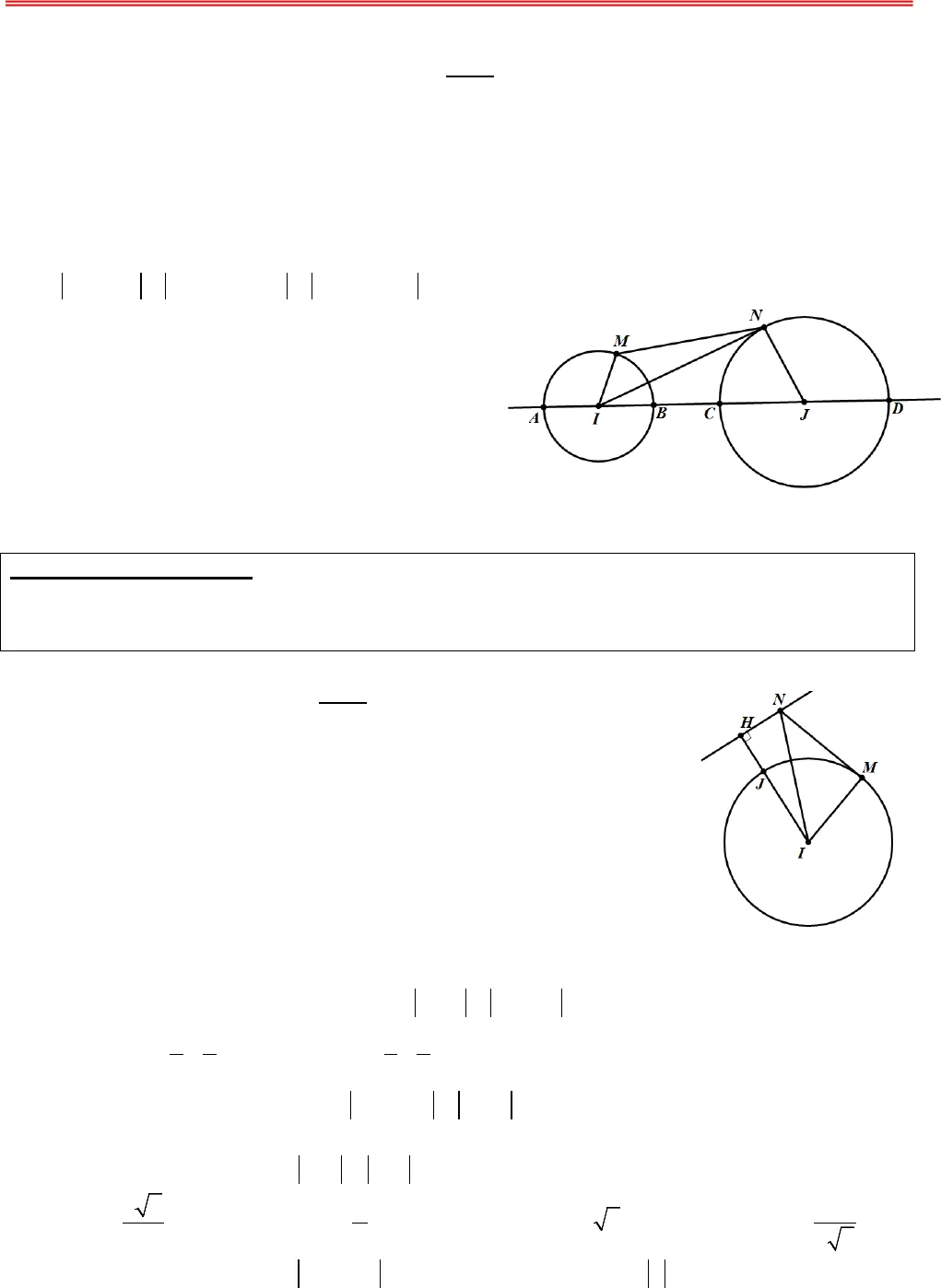https://toanmath.com/ UGiải: Gọi d là đường thẳng đi qua I, J; d cắt đường tròn1()Ttại hai điểm phân biệt A, B (giả sử JA > JB) ; d cắt 2()Ttại hai điểm phân biệt C, D ( giả sử ID > IC). Với điểm M bất khì trên1()Tvà điểm N bất kì trên 2()T.Ta có: 12MN IM IN IM IJ JN R R IJ AD≤+≤++=++=.Đẳng thức xảy ra khi M trùng với A và N trùng với D12MN IM IN IJ IM JN IJ R R BC≥ − ≥ − − = −+ =.Đẳng thức xảy ra khi M trùng với B và N trùng với C. Vậy khi M trùng với A và N trùng với D thì MN đạt giá trị lớn nhất. khi M trùng với B và N trùng với C thì MN đạt giá trị nhỏ nhất. UBÀI TOÁN CÔNG CỤ 3:UCho hai đường tròn()Tcó tâm I, bán kính R; đường thẳng∆không có điểm chung với ()T. Tìm vị trí của điểm M trên()T, điểm N trên ∆sao cho MN đạt giá trị nhỏ nhất.UGiải: Gọi H là hình chiếu vuông góc của I trên dĐoạn IH cắt đường tròn ()Ttại JVới M thuộc đường thẳng∆, N thuộc đường tròn()T, ta có:MN IN IM IH IJ JH const≥ − ≥ −= =.Đẳng thức xảy ra khi ;M HN I≡≡Vậy khi M trùng với H; N trùng với J thì MN đạt giá trị nhỏ nhất.B – BÀI TẬP Câu 1. Trong các số phức thỏa mãn điều kiện 3 2.ziz i+ = +−Tìm số phức có môđun nhỏ nhất? A. 1255zi=−+. B. 1255zi= −. C. 12zi=−+. D. 12zi= −. Câu 2. Trong các số phức zthỏa mãn 24 2z izi−− = −. Số phứczcó môđun nhỏ nhất là A. 32zi= + B.1zi=−+ C. 22zi=−+ D. 22zi= +Câu 3. Cho số phức zthỏa mãn 1−= −z zi. Tìm mô đun nhỏ nhất của số phứcw2 2= +−zi. A. 322. B. 32. C. 32. D. 322. Câu 4. Cho số phức zthỏa mãn 34 1zi−− =. Tìm giá trị nhỏ nhất củaz. A. 6. B. 4. C. 3. D. 5. 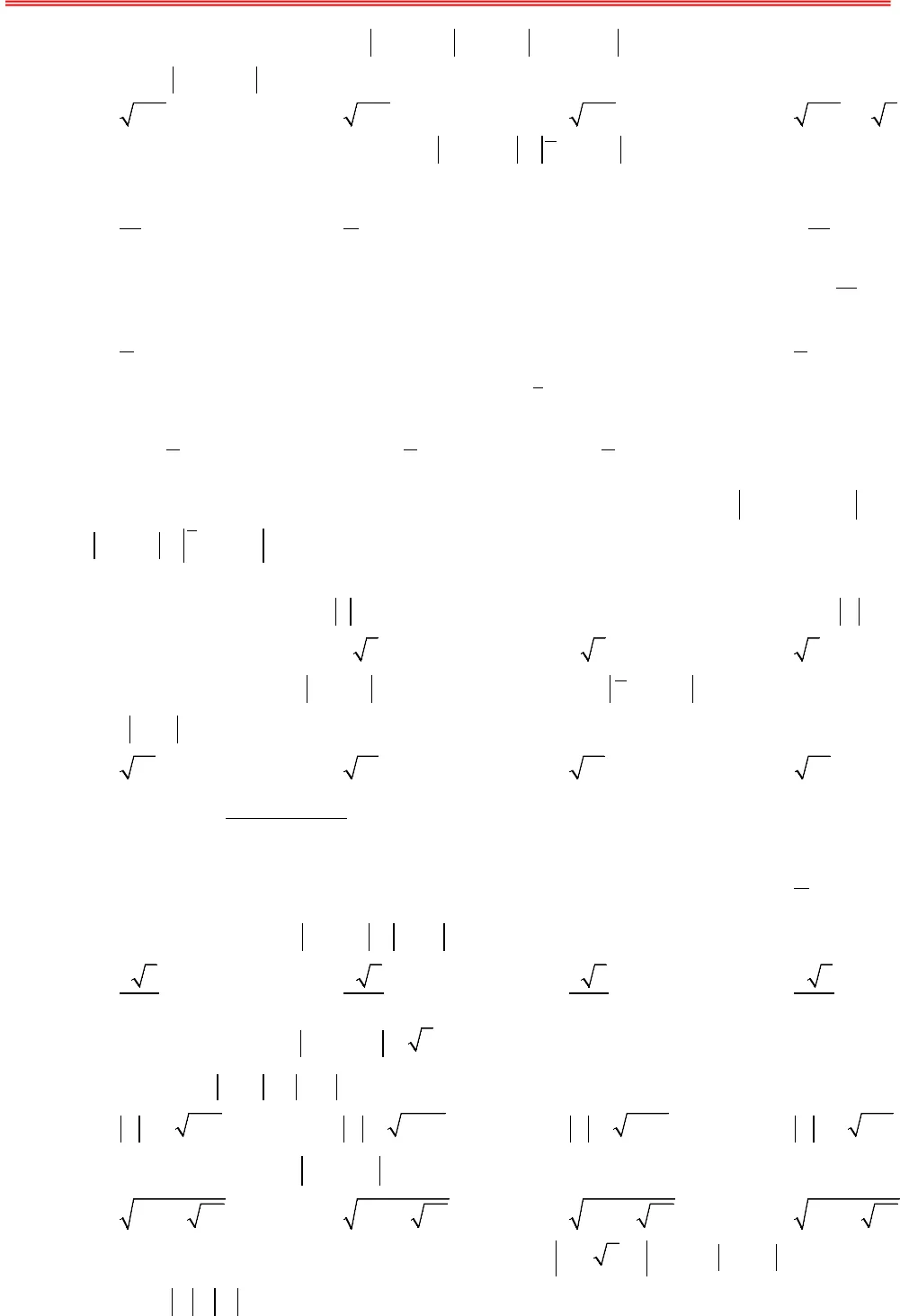https://toanmath.com/ Câu 5. Cho hai số phức 1z,2zthỏa mãn 1352zi−+=và 212 4iz i−+ =. Tìm giá trị lớn nhất của biểuthức1223T iz z= +. A. 313 16+. B. 313. C. 313 8+. D. 313 2 5+. Câu 6. Trong các số phức zthỏa mãn điều kiện 23 12z iz i+ − = +−, hãy tìm phần ảo của số phức cómôđun nhỏ nhất? A. 1013. B. 25. C. 2−. D. 213−. Câu 7. Xét các số phức 134zi= −và 22z mi= +,( )m∈. Giá trị nhỏ nhất của môđun số phức 21zzbằng? A. 25. B. 2. C. 3. D. 15. Câu 8. Số phức znào sau đây có môđun nhỏ nhất thỏa | || 3 4|zz i= −+: A. 322zi=−−. B. 738zi= −. C. 322zi= +. D. 3–4zi= −. Câu 9. Có tất cả bao nhiêu giá trị nguyên của mđể có đúng hai số phức zthỏa mãn( )18zm i− − +=và1 23z iz i−+ = − +. A. 66. B. 130. C. 131. D. 63. Câu 10. Cho các số phức zthoả mãn 2=z. Đặt( )12 12= + −+w iz i. Tìm giá trị nhỏ nhất củaw. A. 2. B. 35. C. 25. D. 5. Câu 11. Cho số phức zthỏa mãn 11zi−− =, số phức wthỏa mãn 23 2wi−− =. Tìm giá trị nhỏ nhất của zw−. A. 17 3+ B.13 3+ C. 13 3− D. 17 3−Câu 12. Cho số phức ( ),12mizmmm i−+= ∈−−. Tìm môđun lớn nhất của .z A. 2. B. 1. C. 0. D. 12. Câu 13. Cho số phức zthỏa mãn 13z izi+− = −. Tính môđun nhỏ nhất củazi−. A. 3510. B.455. C. 355. D. 7510.Câu 14. Cho số phức zthoả mãn 34 5zi−− =. Gọi Mvà mlà giá trị lớn nhất và giá trị nhỏ nhất của biểu thức 222P z zi=+ −−. Tính môđun của số phức .w M mi= + A. 2 309w=. B. 2315w =. C. 1258w =. D. 3 137w =. Câu 15. Cho số phức zthỏa mãn 12 3zi−+ =. Tìm môđun lớn nhất của số phức2.zi− A. +26 8 17. B. −26 4 17. C. +26 6 17. D. −26 6 17. Câu 16. Giả sử 1z,2zlà hai trong số các số phức zthỏa mãn 21iz i+ −=và 122zz−=. Giá trị lớn nhất của 12zz+bằng