Download.vn Học tập Lớp 11 Toán 11

Bạn đang đọc: Bài tập nâng cao giới hạn của dãy số

Bài tập nâng cao giới hạn của dãy số Tài liệu ôn tập chương 3 môn Toán lớp 11

Giới thiệu Tải về Bình luận

• 1

Mua tài khoản Download Pro để trải nghiệm website Download.vn KHÔNG quảng cáo & tải File cực nhanh chỉ từ 79.000đ. Tìm hiểu thêm Mua ngay

Mời quý thầy cô cùng các bạn học sinh lớp 11 cùng tham khảo tài liệu Bài tập nâng cao giới hạn của dãy số được Download.vn đăng tải ngay sau đây.

Bài tập nâng cao giới hạn của dãy số là tài liệu cực kì hữu ích, gồm 14 trang hướng dẫn giải các bài tập nâng cao giới hạn của dãy số được chọn lọc từ các đề thi HSG cấp tỉnh, cấp quốc gia. Hi vọng tài liệu sẽ giúp các bạn học sinh lớp 11 bổ sung kiến thức về phần dãy số trong các kì thi học sinh giỏi và tài liệu tham khảo bổ ích cho bạn đọc. Mời các bạn cùng tham khảo.

Bài tập nâng cao giới hạn của dãy số

Giới hạn của dãy sốNguyễn Minh Tuấn – GV trường THPT Chuyên QBNỘI DUNGI) Phương pháp sử dụng định nghĩa giới hạn dãy số1. Kiến thức sử dụng:Định nghĩa: *lim 0, :n nu L N N n N u L           Sử dụng:- Tiêu chuẩn Cô-si: Dãy {xn} có giới hạn hữu hạn khi và chỉ khi với mọi  > 0, tồn tại số tự nhiên N sao cho với mọi m, n  N ta có |xm– xn| . – Nguyên lý ánh xạ co: Nếu với mọi x, y ta có |f(x) – f(y)|  q|x-y| với q làhằng số 0 q 1 và {xn} bị chặn thì {xn} hội tụ. Đặc biệt nếu |f’(x)|  q 1 thì ta luôn có điều này. Ý tưởng chính: Đánh giá1; 1n nu L q u L q   và1 1; 1n n n nu u q u u q    Phương pháp này thường được dùng khi ta thấy dãy số không tăng, không giảm. 2. Các ví dụ: Bài 1: (Đề thi HSG Quảng Bình) Cho dãy số 113uvà21112n nu u . Tìm giới hạn dãysố?HD: Chứng minh: 1 0nu   Giải phương trình 211 1 32x x x a      Xét2 21 31 12 2 2 2nn n n nu au a u a u a u a             Suy ralim 1 3nu   Bài 2: (Đề dự bị VMO 2008) Cho số thực a và dãy số thực ( )nuxác định bởi:1u avà un+1= ln(3+cosun+ sinun) – 2008 với mọi n = 1, 2, 3, …Chứng minh rằng dãy số (un)có giới hạn hữu hạn.HD: Đặt f(x) = ln(3+sinx+cosx) – 2008 thì cos sin’( )3 sin cosx xf xx x  Từ đó, sử dụng đánh giá | cos sin | 2, | sin cos | 2x x x x   ta suy ra .1232|)(‘|  qxfÁp dụng định lý Lagrange với m > n  N, ta có |um– un| = |f(um-1) – f(un-1)|q|um-1-un-1|…qn-1|um-n+1– u1|.Do dãy (un) bị chặn và q nên dãy (xn) thoả mãn điều kiện Cauchy nên có giới hạn hữu hạn. 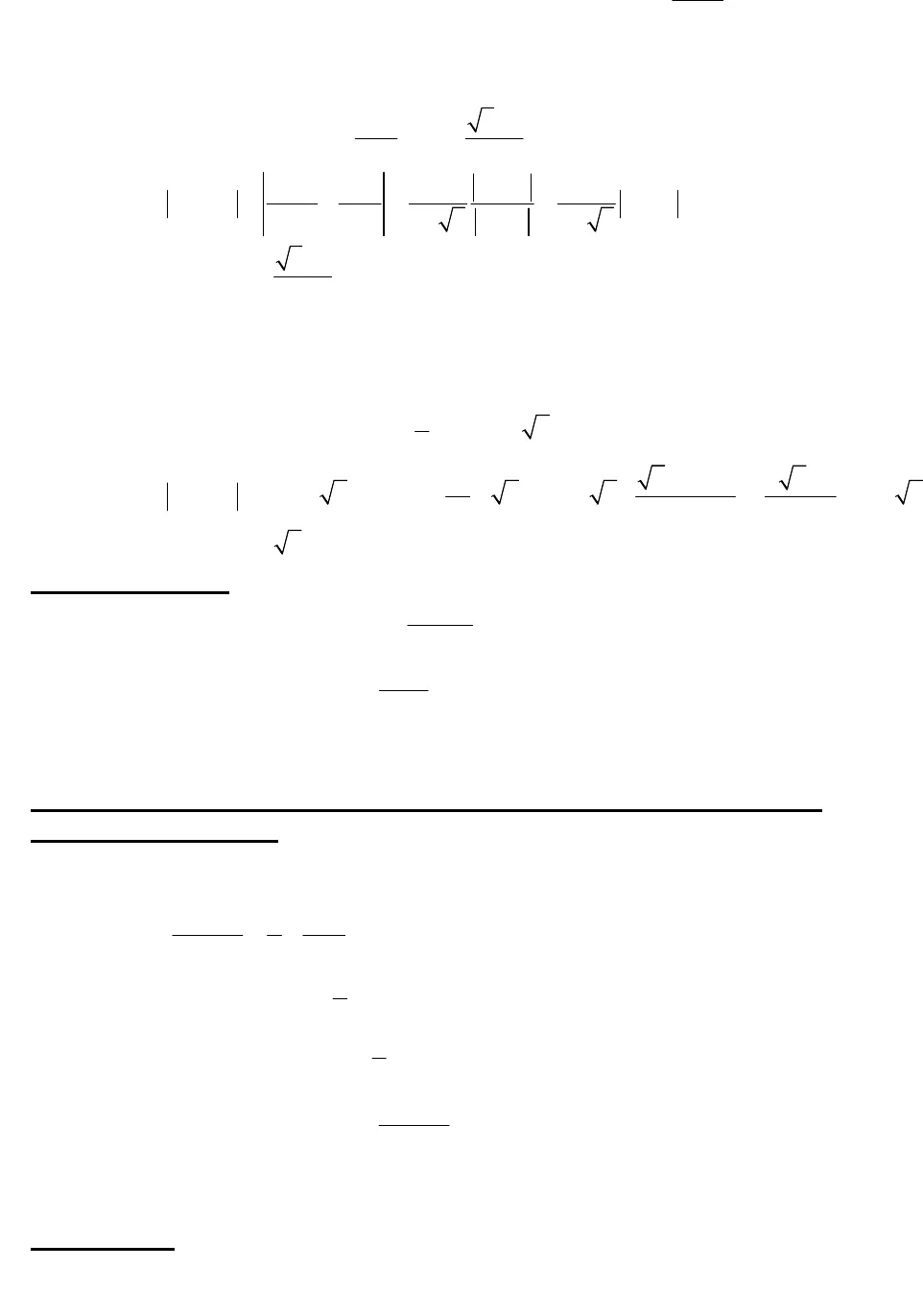Bài tập nâng cao giới hạn của dãy sốGiới hạn của dãy sốNguyễn Minh Tuấn – GV trường THPT Chuyên QBBài 3: (Đề thi vô địch Nga 1982) Cho dãy số 11uvà111nnuu. Tìm giới hạn dãysố?HD: Chứng minh: 0 1nu  Giải phương trình 1 5 11 2x x ax    Xét11 1 2 21 1 11 5 1 5nn nn nu au a u au a u         Suy ra5 1lim2nu a Bài 4: Cho dãy số (un) định bởi u1 (1, 2) và un+1= 1 + un– un2/2. Chứng minh rằng (un) có giới hạn hữu hạn và tìm giới hạn đó. HD: Chứng minh: rằng 1 un3/2 Giải phương trình211 22x x x x a      Xét21 12 1 2 2 1| 2 | |1 2 | | 2 || | | || 2 |2 2 4n nn n n n nu uu a u u u u              Suy ralim 2nu  3. Bài tập tự giải:Bài 1: Cho dãy số 12012u và114 3nnuu. Tìm giới hạn dãy số?Bài 2: Cho dãy số 1u avà 2 2 212012ln 2012 20123n nu u   .Chứng minh dã số có giới hạn.II) Phương pháp sử dụng công thức, tính chất của các dãy số đặc biệt 1. Kiến thức sử dụng:– Tính chất của các dãy số là cấp số cộng, cấp số nhân – Các công thức đối với các dãy số quen thuộc:1 1 1( 1) 1n n n n  11 2 3 … ( 1)2n n n     2 2 2 211 2 3 … ( 1)(2 1)6n n n n      23 3 3 3( 1)1 2 3 …2n nn       Ý tưởng chính: Đưa các dãy số về các dãy số quen thuộc2. Các ví dụ: Giới hạn của dãy sốNguyễn Minh Tuấn – GV trường THPT Chuyên QBBài 1: Cho dãy số 1 1 1...1.2 2.3 ( 1)nunn   .Tìm giới hạn dãy số?HD: 1 1 1 1 1 1 1… 11 2 2 3 1 1nun n n          Suy ralim 1nuBài 2: Cho dãy số   22 2 222 2 21 3 5 .... 2 12 4 6 …. 2nnun       .Tìm giới hạn dãy số?HD:   22 2 222 2 22 (2 1)(4 1)1 2 3 …. 2(4 1)61( 1)(2 1)2( 1)2 4 6 …. 24.6nn n nnnun n nnn            Suy ralim 1nu. Bài 3: Cho dãy số 15uvà15 42nnnuuu. Tìm giới hạn dãy số?HD: Chứng minh: 4nu Ta có:1141 64 12 4 4nnn n nuuu u u       Xét1 1 544 5 6 1n nnnx uu      Suy ralim 4nuBài 4: Cho dãy số 123uvà12(2 1) 1nnnuun u . Tìm giới hạn dãy số1nn nix u?HD: Đặt 1 (2 1)(2 1) 1 12 2 1 2 1n n nnn nv v uu n n        Suy ralim 1nxBài 5: Cho dãy số 11uvà21(0 1)nn nu u a a   . Tìm giới hạn dãy số?HD: Chứng minh: 2 2 2 2 2 2 11 2 31; 1 ; 1 ;…; 1 …nnu u a u a a u a a a          Suy ra:11nnaua Vậy1lim1nuaBài 6: Cho dãy số 12011u và21 1n n nu n u u   . Tìm giới hạn dãy số? HD: Ta có: 211210nn nn uu un   Mặt khác: 1 2 12 2 2( 1)( 1) ( 1)( 1)( 2) 1 1… 2011( 1) 2 2n n nn n n n n n n nu u u un n n n n           Vậy2011lim2nu 