Download.vn Học tập Lớp 12

Bạn đang đọc: Bài tập phương pháp lũy thừa giải hệ phương trình

Bài tập phương pháp lũy thừa giải hệ phương trình Tài liệu ôn tập môn Toán lớp 12

Giới thiệu Tải về Bình luận

• 1

Mua tài khoản Download Pro để trải nghiệm website Download.vn KHÔNG quảng cáo & tải File cực nhanh chỉ từ 79.000đ. Tìm hiểu thêm Mua ngay

Mời quý thầy cô giáo cùng các bạn học sinh lớp 12 cùng tham khảo tài liệu Bài tập phương pháp lũy thừa giải hệ phương trình được Download.vn đăng tải sau đây.

Đây là tài liệu cực kì hữu ích, gồm 19 trang hướng dẫn phương pháp lũy thừa giải hệ phương trình thông qua các bài toán được giải chi tiết. Hy vọng với tài liệu này bạn đọc sẽ “nhớ mặt” được các dạng hệ phương trình có thể sử dụng phương pháp nâng lũy thừa, và hướng sử lý phương trình hệ quả sau đó. Sau đây là nội dung chi tiết, mời các bạn cùng tham khảo và tải tài liệu tại đây.

Bài tập phương pháp lũy thừa giải hệ phương trình

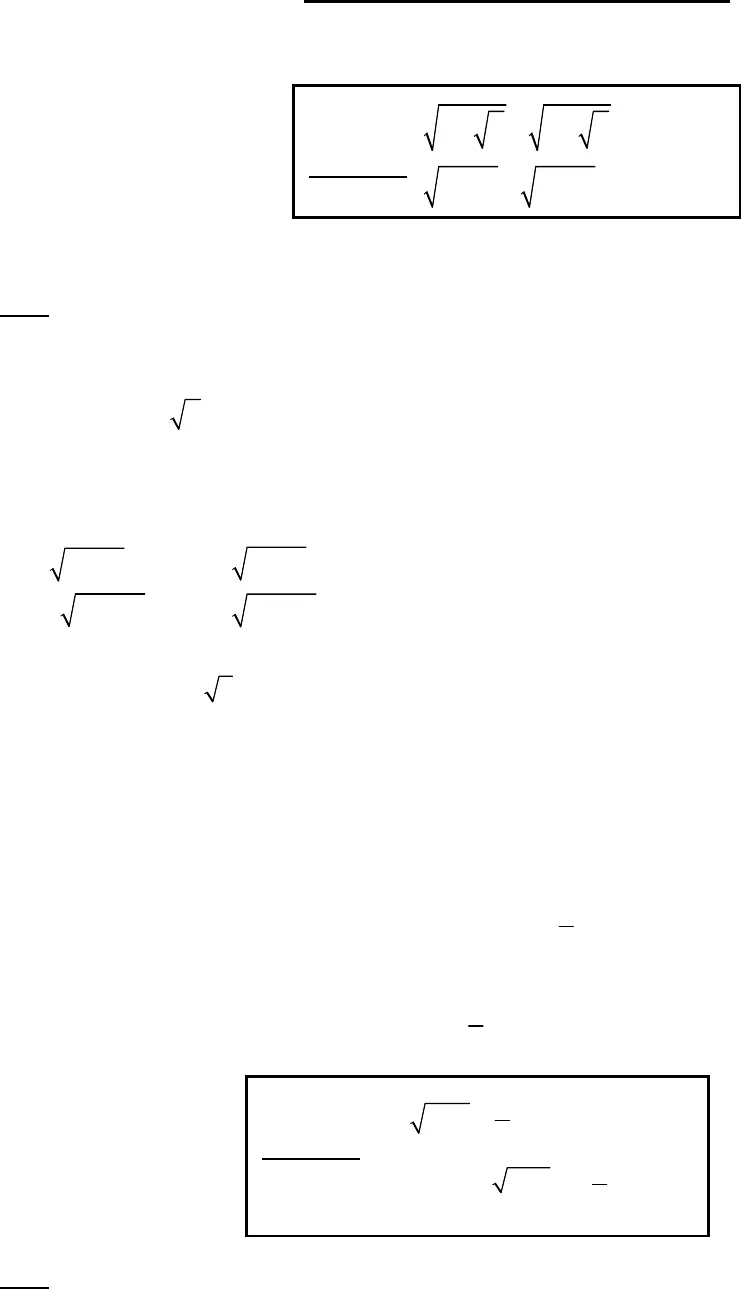1.PHƯƠNG PHÁP LŨY THỪA Giải: Điều kiện : 0x yx y . Nhận xét : Vế trái của phương trình (1) không âm. Bình phương 2 vế từng phương trình ta được 22 4 228x x yx x y      24 2 22 3 8 4x y xx y x    Điều kiện : 0 2 2x  Phương trình 2 23 4 4x y x x    4 4y x  Phương trình 4 2 2 44 64 16x y x x     24 2 44 4 64 16x x x x     532 80 0 62x x y      Vậy nghiệm của hệ phương trình đã cho là 5;62   Giải: Điều kiện : 11xy  Bài toán 1. 2 22 (1)4 2x y x yx y x y      Bài toán 3.    51 (1)232 3 1 24x yy x x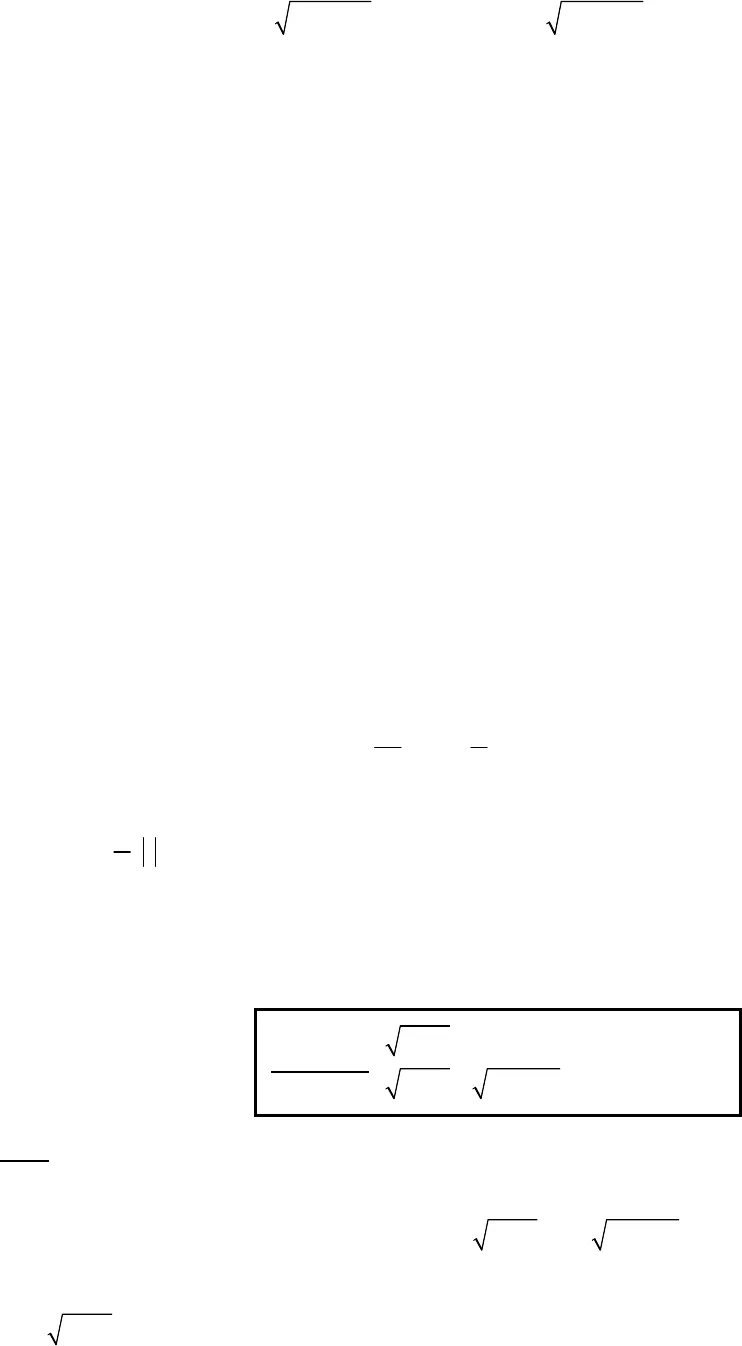      Phương trình  2 22 2 2 4 4x x y    2 24 2 3x y x    Điều kiện tương đương : 2x. Phương trình 2 2 23 4 4 4x y x x    .2 21 1, 1 4y x x y x       Thế (4) vào phương trình (3) ta được : 32 3 2 21 2 1 1 0y y y y y y      6 5 4 3 22 4 2 1 0y y y y y y        24 3 21 3 1 0y y y y y      4 3 21 23 1 0y xy y y y       Xét phương trình : 4 3 23 1 0y y y y     Nếu0 1y x  , không thỏa hệ.Xét0 :yphương trình  221 13 0y yy y         Đặt 1, 2.t y ty  Phương trình trên trở thành :21 0t t  , vô nghiệm.Vậy nghiệm của hệ phương trình đã cho là 1;2Giải: Điều kiện : 3 2 0x yx y  . Phương trình 2 1 3 2x y x y    .2 2 1 3x y x y    .Điều kiện :2 1x y .Thế (3) vào phương trình (1) ta được : Bài toán 5.  0 (1)3 2 1 2x y x yx y x y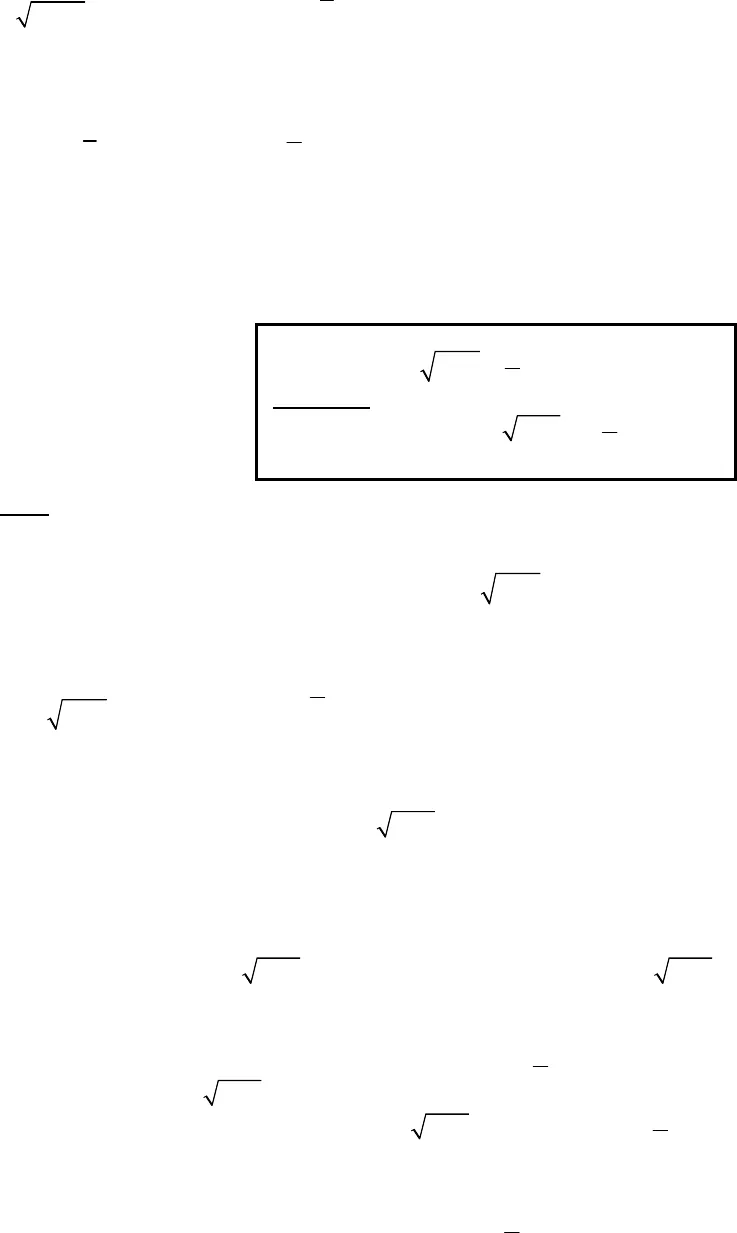       4 1 0 4 1 4x y y x      Thế (4) vào phương trình (3) ta được : 2 5 1 6 2x x  2135 1 9 6 1xx x x   212,391 39 11 2 0xx loaix yx x     Vậy nghiệm của hệ phương trình đã cho là 1;3Giải: Điều kiện : 11yx  . Phương trình 1 2 2 1 5x y   .2 1 2 5y x      2524 1 4 20 25 3xy x x   Phương trình 2 4 4 8 3 1 1 4y x x     Thế (3) vào phương trình (4) ta được : 24 20 24 8 3 1 0x x x x     4 3 2 8 3 1 0x x x x       4 3 2 2 1 0x x x     33452 1 2 , vi x2x yx x loai      Vậy nghiệm của hệ phương trình đã cho là 33;4   Bài toán 6.    51 (1)232 3 1 24x yy x x      