Download.vn Học tập Lớp 11 Toán 11

Bạn đang đọc: Bài tập trắc nghiệm tổ hợp và xác suất nâng cao

Bài tập trắc nghiệm tổ hợp và xác suất nâng cao Tài liệu ôn tập môn Toán lớp 11

Giới thiệu Tải về Bình luận

• 1

Mua tài khoản Download Pro để trải nghiệm website Download.vn KHÔNG quảng cáo & tải File cực nhanh chỉ từ 79.000đ. Tìm hiểu thêm Mua ngay

Bài tập trắc nghiệm tổ hợp và xác suất nâng cao là tài liệu cực kì hữu ích mà Download.vn muốn giới thiệu đến các bạn học sinh lớp 11 cùng tham khảo.

Đây là tài liệu hay, bổ ích để các em có thể rèn luyện nhiều hơn với các bài toán tổ hợp và xác suất ở mức độ khó và rất khó. Tài liệu phù hợp với các em học sinh khối 11 học nâng cao, các em học sinh lớp 12 ôn thi THPTQG môn Toán và các em học sinh ôn thi HSG Toán. Sau đây là nội dung chi tiết, mời các bạn cùng tham khảo và tải tài liệu tại đây.

Bài tập trắc nghiệm tổ hợp và xác suất nâng cao

Email: [email protected] Câu 1. Cho 5 điểm đồng phẳng sao cho các đường thẳng đi qua các cặp điểm trong 5 điểm đó không có 2 đường thẳng nào song song, vuông góc hay trùng nhau. Qua mỗi điểm ta vẽ các đường vuônggóc với tất cả các đường thẳng nối 2 điểm trong 4 điểm còn lại. Không kể 5 điểm đã cho số giaođiểm của các đường thẳng vuông góc đó nhiều nhất là bao nhiêu?A. 310. B. 330. C. 360. D. 325.Lời giải Tác giả : Chu Viết Tấn,Tên FB: Chu Viết TấnChọn A Gọi 5 điểm đó là, , , ,A B C D ECó246Cđường thẳng không đi quaAnên từAkẻ được 6 đường thẳng vuông góc với 6đường thẳng đó. Tương tự từBkẻ được 6 đường thẳng vuông góc với 6 đường thẳng không điqua B. Đáng lẽ ra 2 nhóm đường thẳng này cắt nhau tại6 6 36 điểm ( Không kể,A B).Nhưng vì có233Cđường thẳng không đi qua 2 điểm,A Bnên 3 đường thẳng vuông góc vẽtừ A và 3 đường thẳng vuông góc vẽ từ B đôi một song song với nhau nên số giao điểm của 2nhóm đường thẳng vuông góc này chỉ còn 36-3=33 điểm. Có2510Ccách chọn các cặp điểmnhư vậy nên có 330 giao điểm của các đường thẳng vuông góc. Thế nhưng cứ mỗi 3 điểm như, ,A B Cthì 3 đường cao của tam giác này trong số các đường vuông góc đó lại đồng quy tại 1điểm ( thay vì cắt nhau tại 3 điểm) nên số giao điểm giảm đi 2. Vì có3510Ctam giác như tamgiác ABC nên số giao điểm giản đi 20. Vậy số giao điểm nhiều nhất của các đường thẳng vuônggoác là 330-20=310.Mở rộng: Bài này có thể tổng quát cho n điểm (n>2)[email protected]Câu 2. Từ các chữ số thuộc tập  1;2;3;4;5;6;7X có thể lập được bao nhiêu số tự nhiên chẵn gồm 5chữ số khác nhau sao cho mỗi số tự nhiên đó đều chia hết cho 9. A. 96. B. 144. C. 72. D. 120.Lời giải Tác giả : Phạm Thành Trung,Tên FB: Phạm Thành TrungChọn ATa có nhận xét1 2 3 4 5 6 7 28      là số khi chia cho 9 có dư là 1.Vậy khi đó để chọn ra số tự nhiên có 5 chữ số chia hết cho 9 ta cần loại đi trong tậpXhai chữsố có tổng khi chia cho 9 dư là 1.Do đó có hai trường hợp loại đi hai số có tổng chia cho 9 dư 1 là   3;7 ; 4;6Khi loại đi cặp 3;7ta có:+ Chọn số cho vị trí hàng đơn vị có 3 cách.+ Chọn số cho các vị trí còn lại có4!cách.Trường hợp này có3.4! 72số.Khi loại đi cặp 4;6ta có:+ Chọn số cho vị trí hàng đơn vị có 1 cách.+ Chọn số cho các vị trí còn lại có4!cách.Trường hợp này có4! 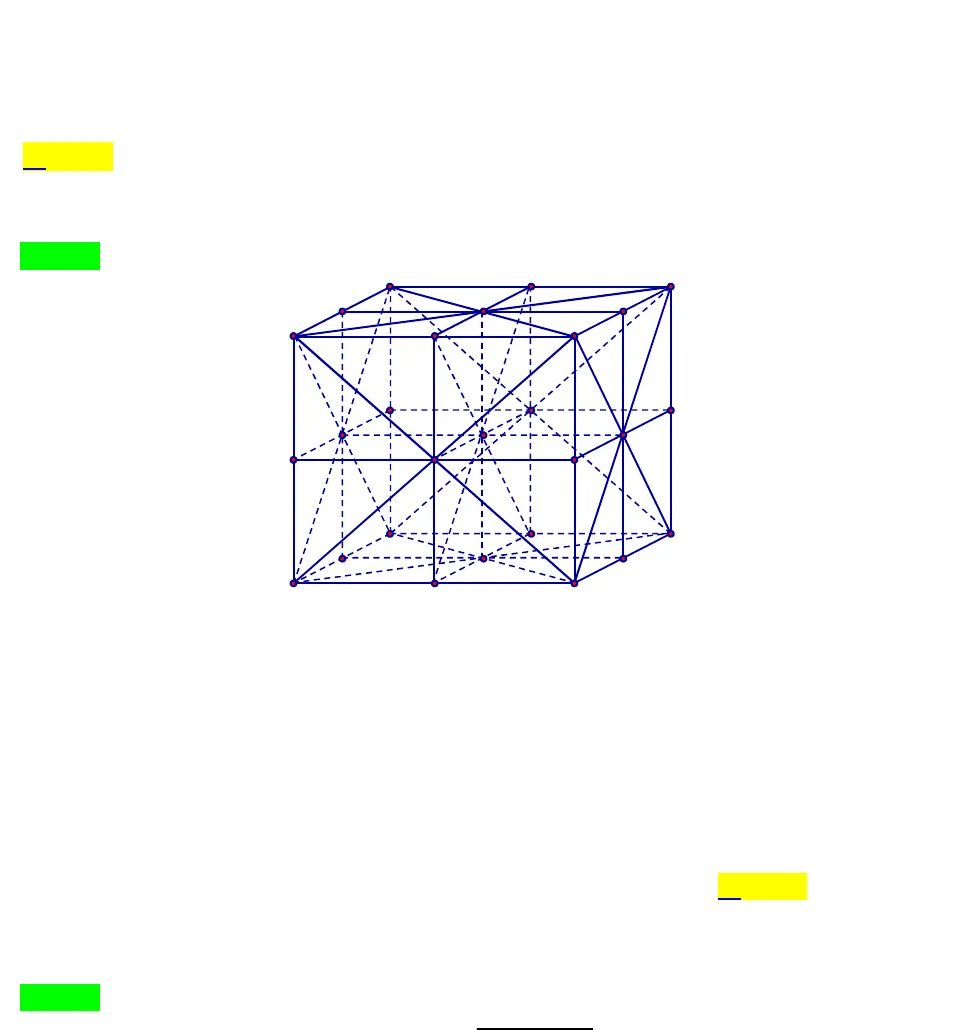24số.Vậy có tất cả72 24 96 số thỏa mãn yêu cầu.[email protected]Câu 3. (THPT Chuyên Hùng Vương-Phú Thọ-lần 1-NH2017-2018) Một khối lập phương có độ dài cạnh là2cmđược chia thành8khối lập phương cạnh1cm. Hỏi có bao nhiêu tam giác được tạothành từ các đỉnh của khối lập phương cạnh1cm. A. 2876. B. 2898. C. 2915. D. 2012.Lời giải Tác giả : Nguyễn Thúy Hằng, FB: Hằng-RuBy-NguyễnChọn D Có tất cả27điểm.Chọn3điểm trong27có3272925.C Có tất cả 8.2 6.2 4.2 4 3 2 2 2 49       bộ ba điểm thẳng hàng.Vậy có2925 49 2876 tam giác.[email protected]Câu 4. Cho tập {0,1, 2,3,4,5,6,7,8,9}A.Từ các phần tử của tậpAcó thể lập được bao nhiêu số có 6chữ số đôi một khác nhau mà trong đó hai số chẵn không thể đứng cạnh nhau? A.26880. B.27360. C.34200. D.37800. Lời giải Tácgiả :Trần Quốc An, FB: TranQuocAnChọn DGiả sử số có 6 chữ số thỏa đề bài có dạng1 2 3 4 5 6M a a a a a a.Nhận xét : Trong các vị trí 1 2 3 4 5 6, , , , ,a a a a a acó tối đa 3 chữ số là số chẵn được lấy từ tập.ATH1 : Số Mchỉ chứa 1 chữ số chẵn+1achẵn : 1acó 4 cách chọnCác vị trí2 3 5, ,..,a a alà số lẻ nên có5!cách xếpTH này có :4.5! 480cách chọn.+1alẻ : 1acó 5 cách chọnChọn một chữ số chẵn và 4 chữ số lẻ và xếp chúng ở 5 vị trí2 3 5, ,..,a a anhư sau1 45 4. .5!C CcáchTH này có :1 45 45. . .5! 3000C C cách chọn.TH2: Số Mcó chứa 2 chữ số chẵn .+1achẵn : 1acó 4 cách chọnVị trí2alà số lẻ nên2acó 5 cách chọn .Chọn một chữ số chẵn và 3 số lẻ và xếp chúng vào 4 vị trí còn lại có1 34 4. .4!C CcáchTH này có :1 34 44.5. . .4! 7680C C cách chọn.+1alẻ :1acó 5 cách chọnỞ các vị trí2 3 5, ,..,a a acó 3 chữ số lẻ , ta tạo được 4 vách ngăn , chọn hai chữ số chẵn và đặtvào 2 trong 4 vách ngăn đó,chọn 3 chữ số lẻ trong 4 số lẻ đặt ở 3 vị trí còn lại có2 2 35 4 4. .2!. .3!C C Ccách.TH này có2 2 35 4 45. . .2!. .3! 14400C C C cách chọn.TH3: Số Mcó chứa 3 chữ số chẵn .+1achẵn : 1acó 4 cách chọnVị trí2alẻ nên2acó 5 cách chọnỞ các vị trí3 4 5 6, , ,a a a acó 2 chữ số lẻ , ta tạo được 3 vách ngăn , chọn hai chữ số chẵn và đặtvào 2 trong 3 vách ngăn đó,chọn 2 chữ số lẻ trong 4 số lẻ đặt ở 2 vị trí còn lại có2 2 24 3 4. .2!. .2!C C Ccách.TH này có2 2 24 3 44.5. . .2!. .2! 8640C C C cách chọn.+1alẻ :1acó 5 cách chọnỞ các vị trí2 3 5, ,..,a a acó 2 chữ số lẻ , ta tạo được 3 vách ngăn , chọn ba chữ số chẵn và đặt vào3 vách ngăn đó,chọn 2 chữ số lẻ trong 4 số lẻ đặt ở 2 vị trí còn lại có3 25 4.3!. .2!C Ccách.TH này có3 25 45. .3!. .2! 3600C C cách chọnVậy có : 480 3000 7680 14400 8640 3600 37800     cách chọn thỏa yêu cầu bài toán.Email: [email protected]Câu 5. Cho đa giác đều 20 cạnh nội tiếp đường tròn (O). Xác định số hình thang có 4 đỉnh là các đỉnh của đa giác đều. A. 765 B. 720 C. 810 D. 315 Lời giải Tác giả: Nguyễn Văn Mến – face: Nguyễn Văn MếnHình thang luôn có trục đối xứng đi qua tâm nên ta chỉ xét trục đối xứng vuông góc với hai đáycủa hình thang trong hai trường hợpTh1: Trục đối xứng của hình thang đi qua hai đỉnh của đa giác đều Chọn một trục đối xứng có 10 cáchMỗi trục đối xứng như vậy ta có29Ccách chọn các đỉnh của hình thang nhân trục đối xứng đóSuy ra2910. 360C hình thang có trục đối xứng đi qua các đỉnh đa diệnTh2: Trục đối xứng không đi qua đỉnh của đa giác đều Chọn một trục đối xứng như vậy ta có 10 cáchMỗi trục đối xứng như vậy ta có210Ccách chọn các đỉnh của hình thang nhận trục đối xứng đóSuy ra21010. 450C hình thang có trục đối xứng không qua các đỉnh của đa giác đều