Download.vn Học tập Lớp 12
Bạn đang đọc: Bài tập trắc nghiệm ứng dụng của tích phân
Bài tập trắc nghiệm ứng dụng của tích phân Tài liệu ôn tập môn Toán lớp 12
Giới thiệu Tải về Bình luận
- 1
Mua tài khoản Download Pro để trải nghiệm website Download.vn KHÔNG quảng cáo & tải File cực nhanh chỉ từ 79.000đ. Tìm hiểu thêm Mua ngay
Mời quý thầy cô giáo cùng các bạn học sinh lớp 12 tham khảo tài liệu Bài tập trắc nghiệm ứng dụng của tích phân được Download.com.vn đăng tải ngay sau đây.
Đây là tài liệu hữu ích, gồm 229 trang tuyển chọn và phân dạng các bài tập trắc nghiệm có đáp án chi tiết các chủ đề ứng dụng của tích phân để tính diện tích, thể tích và giải quyết các bài toán thực tế. Hi vọng đây sẽ là tài liệu hữu ích dành cho các bạn học sinh có thêm nhiều tài liệu học tập, củng cố kiến thức để đạt được kết quả cao trong các bài kiểm tra, bài thi THPT Quốc gia 2020 sắp tới. Đồng thời đem đến cho các thầy cô có thêm nhiều tài liệu giảng dạy. Nội dung chi tiết mời các bạn cùng theo dõi bài viết dưới đây.
Bài tập trắc nghiệm ứng dụng của tích phân
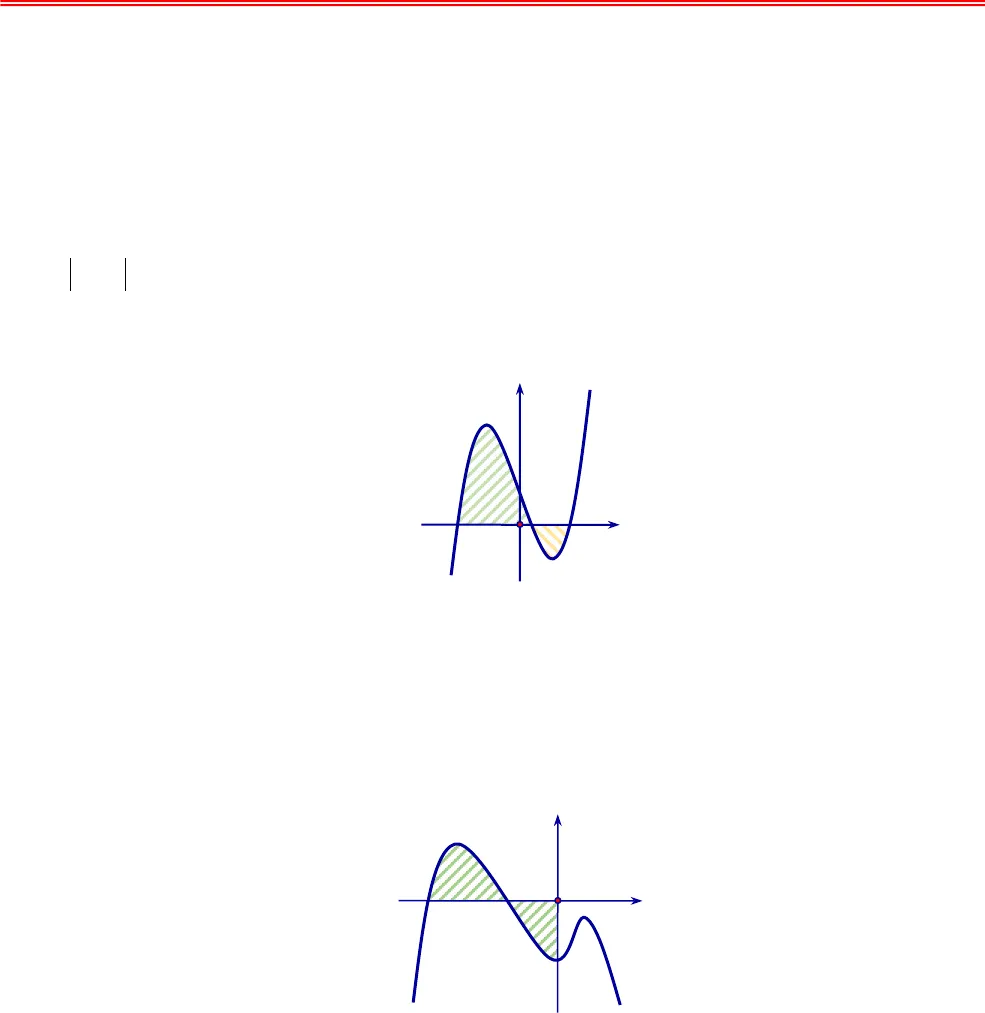https://toanmath.com/ BÀI TẬP Dạng 1:Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số ()y fx=, trục hoành và hai đườngthẳng ( ),x ax ba b= = Câu 1. Viết công thức tính diện tích hình phẳng được giới hạn bởi đồ thị hàm số ( )y fx=, trục Oxvà các đường thẳng( ),.x ax b a b= = A.( )baf x dx∫. B. ( )2baf x dx∫. C. ( )baf x dx∫. D. ( )baf x dxπ∫.Câu 2. Cho hàm số ( )y fx=liên tục trên và có đồ thị như hình vẽ bên. Hình phẳng được đánh dấu trong hình vẽ bên có diện tích làA.( ) ( )ddbcabfx x fx x−∫∫. B.( ) ( )ddbcabfx x fx x+∫∫.C.( ) ( )ddbcabfx x fx x−+∫∫. D.( ) ( )ddbbacfx x fx x−∫∫.Câu 3. Cho hàm số ( )fxliên tục trên , có đồ thị như hình vẽ. Gọi Slà diện tích hình phẳngđược giới hạn bởi đồ thị hàm số ( )fx, trục hoành và trục tung. Khẳng định nào sau đây đúng?A.( ) ( )0dddcdS fx x fx x= −∫∫. B.( ) ( )0dddcdS fx x fx x=−−∫∫.C.( ) ( )0dddcdS fx x fx x=−+∫∫. D.( ) ( )0dddcdS fx x fx x= +∫∫.Câu 4. Diện tích của hình phẳng ( )Hđược giới hạn bởi đồ thị hàm số( )y fx=, trục hoành vàhai đường thẳng xa=,xb=( )ab(phần tô đậm trong hình vẽ) tính theo công thức: Oxycba( )y fx=Oxycd( )y fx=ỨNG DỤNG DIỆN TÍCH
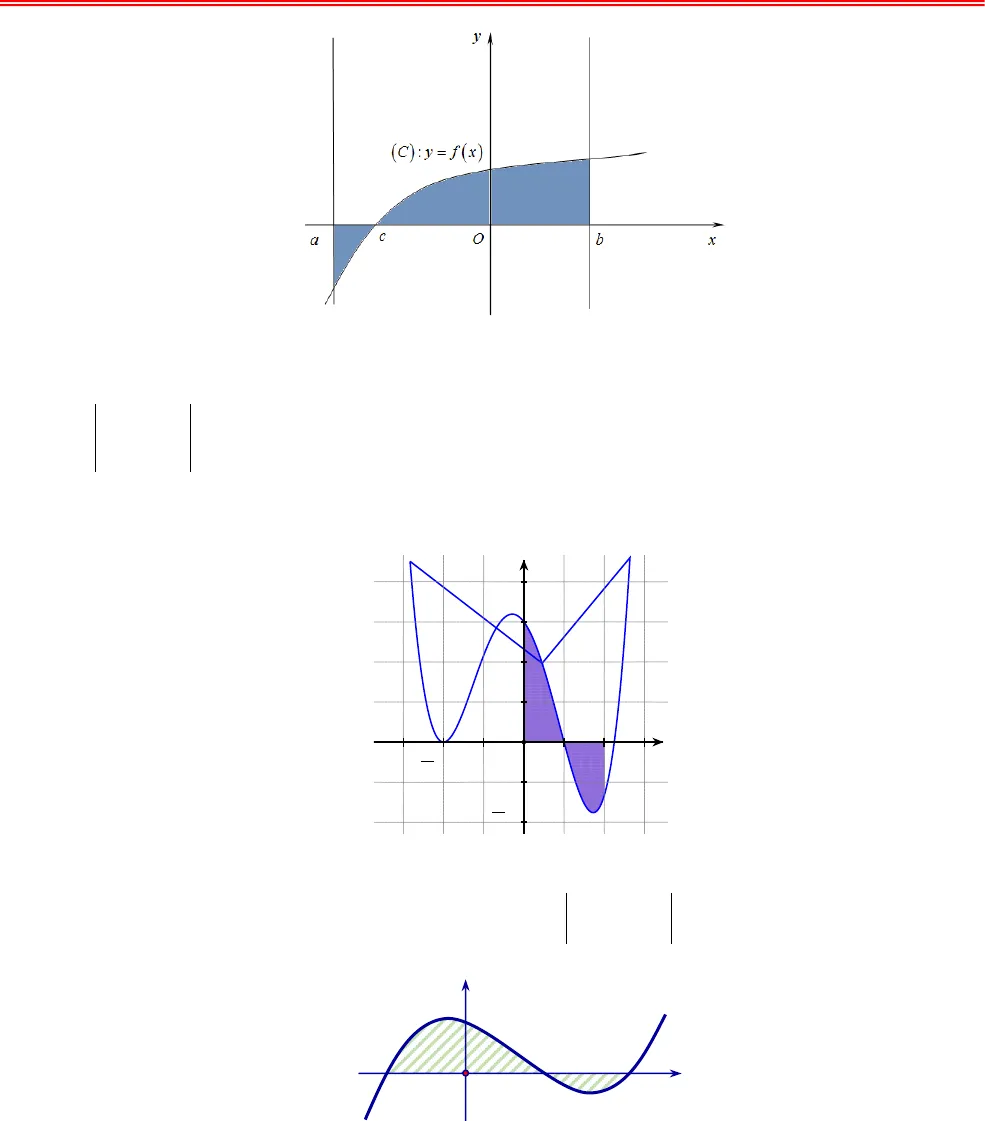https://toanmath.com/ A.( )dbaS fx x=∫. B. ( ) ( )ddcbacS fx x fx x=−+∫∫. C.( )dbaS fx x=∫. D. ( ) ( )ddcbacS fx x fx x= +∫∫.Câu 5. Cho hàm số ( )y fx=liên tục trên và có đồ thị( )Clà đường cong như hình bên. Diệntích hình phẳng giới hạn bởi đồ thị( )C, trục hoành và hai đường thẳng0=x,2=x(phần tô đen) là A.( )20dfx x∫. B. ( ) ( )1201ddfx x fx x−+∫∫. C.( ) ( )1201ddfx x fx x−∫∫. D. ( )20dfx x∫.Câu 6. Gọi S là diện tích miền hình phẳng được tô đậm trong hình vẽ bên. Công thức tính S là A.( ) ( )1211ddS fx x fx x−= +∫∫. B. ( ) ( )1211ddS fx x fx x−= −∫∫. C.( )21dS fx x−=∫. D. ( )21dS fx x−= −∫.Câu 7. Diện tích hình phẳng được giới hạn bởi đồ thị hàm số 323yx x, trục hoành và haiđường thẳng 1x ,4x là xy22321OOxy211−( )y fx=
https://toanmath.com/ A.534 B. 514 C. 494 D. 252Câu 8. Diện tích hình phẳng được giới hạn bởi đồ thị hàm số 4234yx x , trục hoành và haiđường thẳng 0x ,3xlà A.1425 B.1435 C. 1445 D. 1415Câu 9. Diện tích hình phẳng được giới hạn bởi đồ thị hàm số 12xyx, trục hoành và đườngthẳng 2x là A.3 2ln 2 B.3 ln 2 C. 3 2ln 2 D. 3 ln 2Câu 10. Diện tích hình phẳng giới hạn bởi đồ thị hàm số cosyx=, trục tung, trục hoành và đường thẳng xπ=bằng A.3. B. 2. C. 4. D. 1. Câu 11. Diện tích hình phẳng được giới hạn bởi đồ thị hàm số cos2yx, trục hoành và hai đườngthẳng 0,2xxlà A.2 B. 1 C. 3 D. 4Câu 12. Tính diện tích Scủa hình phẳng giới hạn bởi đồ thị hàm sốeexxy−= +, trục hoành, trục tung và đường thẳng 2x = −. A.42e1eS+=(đvdt). B. 4e1eS−=(đvdt). C. 2e1eS−=(đvdt). D. 42e1eS−=(đvdt). Câu 13. Diện tích Scủa hình phẳng giới hạn bởi đồ thị hàm số2yx=, trục hoànhOx, các đường thẳng 1x =,2x =là A.73S=. B. 83S =. C. 7S =. D. 8S =.Câu 14. Diện tích hình phẳng giới hạn bởi hàm số 221= +yxx, trục Oxvà đường thẳng1=xbằngln(1 )ab bc−+với ,,abclà các số nguyên dương. Khi đó giá trị của abc++là A. 11 B. 12 C. 13 D. 14 Câu 15. Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số 12xyx+=−và các trục tọa độ Ox, Oy ta được: ln 1bSac= −. Chọn đáp án đúng A. a+b+c=8 B. a>b C. a-b+c=1 D. a+2b–9=c Câu 16. Cho parabol ( )Pcó đồ thị như hình vẽ:Oxy13241−