Download.vn Học tập Lớp 12 Thi THPT Quốc Gia Toán
Bạn đang đọc: Bài toán cực trị hình học trong không gian
Bài toán cực trị hình học trong không gian Tài liệu ôn thi THPT Quốc gia môn Toán
Giới thiệu Tải về Bình luận
- 1
Mua tài khoản Download Pro để trải nghiệm website Download.vn KHÔNG quảng cáo & tải File cực nhanh chỉ từ 79.000đ. Tìm hiểu thêm Mua ngay
Mời quý thầy cô giáo cùng các bạn học sinh lớp 12 cùng tham khảo tài liệu Bài toán cực trị hình học trong không gian được chúng tôi đăng tải ngay sau đây.
Bài toán cực trị hình học trong không gian trình bày phương pháp về các bài toán cực trị hình học trong không gian như: Tìm điểm, tìm độ dài để thể tích đa diện, độ dài đoạn thẳng đạt lớn nhất, nhỏ nhất, hướng dẫn phương pháp giải bài toán cực trị hình học không gian thông qua các ví dụ có lời giải chi tiết. Mời các bạn cùng tham khảo và tải tài liệu tại đây.
Bài toán cực trị hình học trong không gian
Sáng kiến kinh nghiệm năm họcTrường THPT Phù CừGiáo viên; Quách Đăng Thăng – Tổ Toán – Tin 2NỘI DUNGI. CƠ SỞ LÝ THUYẾTMuốn tìm giá trị lớn nhất hoặc giá trị nhỏ nhất của một đại lượng hìnhhọc biến thiên f ta có thể sử dụng một trong các phương pháp sau:1. Vận dụng các kết quả hình học cơ bản để so sánh trực tiếp f với một đạilượng không đổi cho trước. Sau đây là một vài kết quả cơ bản:a.∀A, B,C, AB + BC≥CA. Đẳng thức xảy ra khi và chỉ khi A, B, C thẳnghàng theo thứ tự đó.b. NếuABC vuông tại A thì: AB BC và AC BC.c. Trong một tam giác, đối diện với góc lớn hơn là cạnh lớn hơn và ngược lại.d. Trong tất cả các đoạn thẳng vẽ từ một điểm M đến mặt phẳng( )α(hoặc đường thẳng d) không chứa điểm M thì đoạn vuông góc là đoạn thẳngngắn nhất.e. Đoạn thẳng vuông góc chung của hai đường thẳng chéo nhau là đoạn thẳngngắn nhất nối liền hai điểm lần lượt thuộc hai đường thẳng đó.2. Nếu f được biểu thị thành một biểu thức của nhiều đại lượng biến thiên vàcác đại lượng này lại được ràng buộc với nhau bởi một hệ thức liên hệ thì ta sửdụng các bất đẳng thức đại số để tìm giá trị lớn nhất (giá trị nhỏ nhất) của f. Cácbất đẳng thức thường dùng là:a. Bất đẳng thức Cô si:∀1 2, ,na a a…≥0,1 11 2nnna a aa a an+ +≥……Dấu đẳng thức xảy ra⇔1 1na a a= =…b. Bất đẳng thức Bu–nhi-a-côp-xki:∀1 2, ,na a a…,1 2, ,nx x x…,2 2 2 2 2 2 21 1 2 2 1 1 2 2( ) ( )( )( )n n n na x a x a x a x a x a x+ + ≤ + + +…Dấu bằng xảy ra khi⇔∃k∈R,1 1 2 2, ,...,n nx ka x ka x ka= = =3. Nếu f được biểu thị bằng một hàm số của một biến số x thì ta sử dụngphương pháp khảo sát hàm số để tìm giá trị lớn nhất (giá trị nhỏ nhất) của hàmsố đó trên miền xác định của nó, từ đó suy ra giá trị lớn nhất (giá trị nhỏ nhất)của f.4. Phương pháp tọa độ trong không gian a. Trong không gian oxyz: Xét hệ toạ độ Đề các vuông góc giả sử A(x1,y1,z1),B(x2,y2,z2) thì1 2 2 1 2 1( , , )AB x x y y z z= − − −và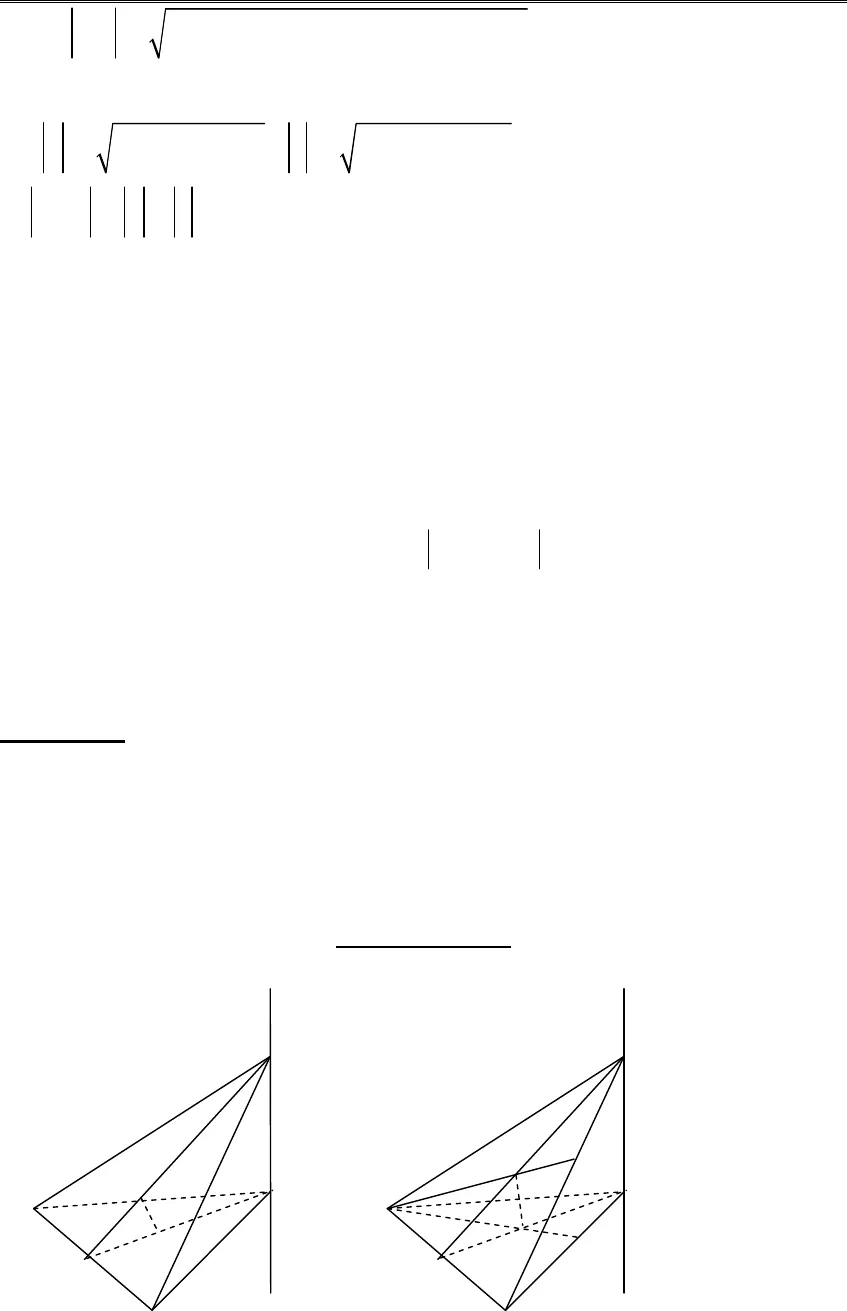
Sáng kiến kinh nghiệm năm họcTrường THPT Phù CừGiáo viên; Quách Đăng Thăng – Tổ Toán – Tin 32 2 21 2 1 2 1 2( ) ( ) ( )AB x x y y z z= − + − + −b. Cho 2 vectơ:1 1 1( , , )u x y z=,2 2 2( , , )v x y z=*2 2 21 1 1u x y z= + +;2 2 22 2 2v x y z= + +*u v u v+ ≤ + (dấu “=” xảy ra khi và chỉ khi,u v cùng chiều hoặc 1 trong 2vectơ bằng0).* Điều kiện để hai véc tơavà()0b b ≠ cùng phương làt R∃ ∈đểa=tb* Điều kiện để ba véc tơa;cvàbkhông đồng phẵng là; . 0a b c ≠ * Điều kiện để ba véc tơa;cvàbđồng phẵng là; . 0a b c = * 1 2 1 2 1 2. 0 0u v u v x x y y z z⊥ ⇔ = ⇔ + + = * Cho ABCThì AB+BCBC≥ vàAB BC AC− ≤dấu đẳng thức sãy rakhi ba điểm A;B;C thẳng hàngII. MỘT SỐ BÀI TOÁN ĐIỂN HÌNHBài toán 1: Cho tam giác cân ABC, AB=AC. Một điểm M thay đổi trên đườngthẳng vuông góc với mặt phẳng (ABC) tại A (M không trùng với điểm A)a) Tìm quỹ tích trọng tâm G và trực tâm H của tam giác MBCb) Gọi O là trực tâm của tam giác ABC, hãy xác định vị trí của M để thể tích tứdiện OHBC đạt giá trị lớn nhất.(Đại học Quốc gia Hà Nội – 1997)Hướng dẫn giảiMABCIHODEMABCIGG’
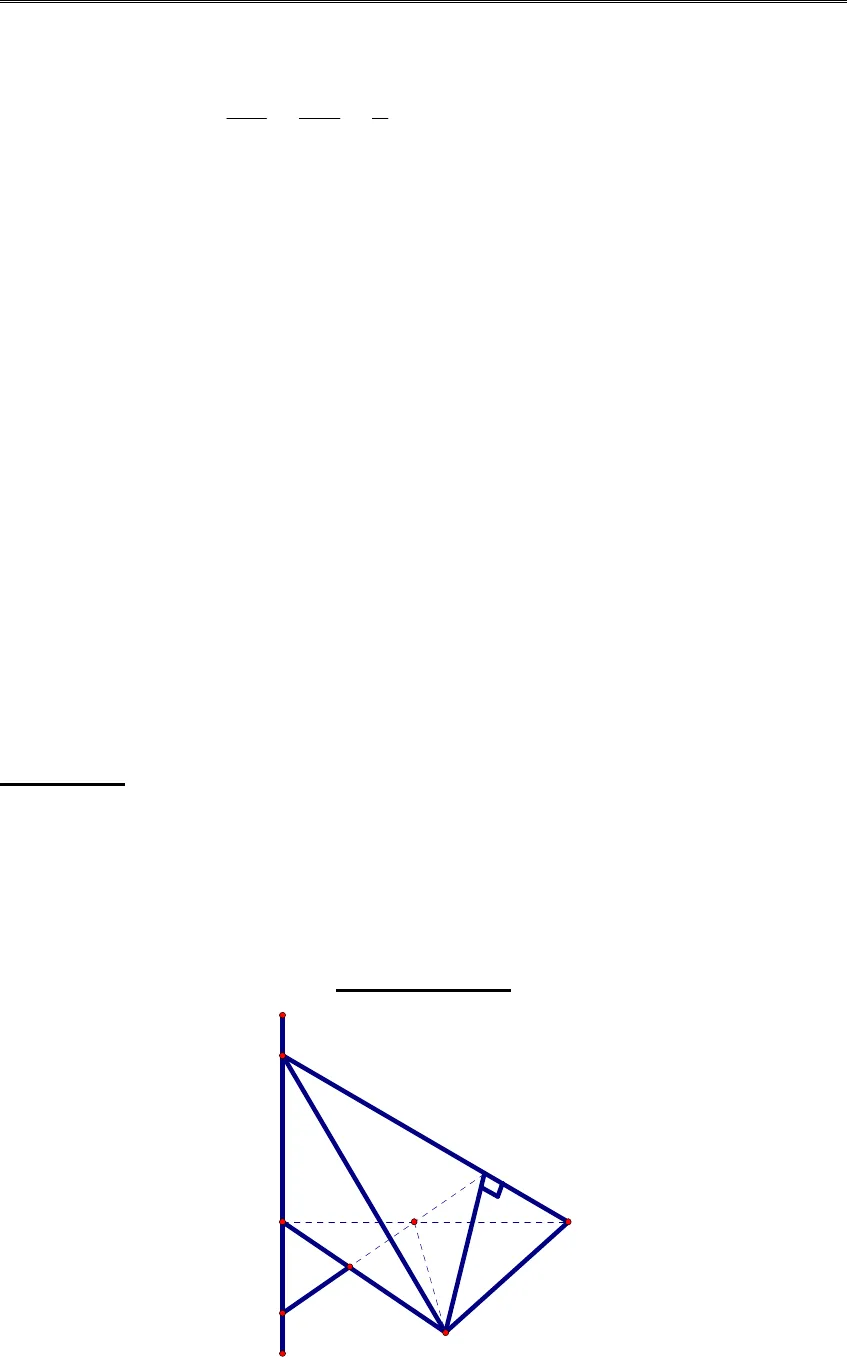Sáng kiến kinh nghiệm năm họcTrường THPT Phù CừGiáo viên; Quách Đăng Thăng – Tổ Toán – Tin 4a) Gọi I là trung điểm của BC, trọng tâm∆MBC là G, trọng tâm của ABC là,G.Trong∆MIA ta có :,13IG IGIM IA= =suy ra,GG// MADo đó G nằm trên đường vuông góc với mặt phẳng (ABC) tại,G, đó là đườngthẳng chứa,GG.Với MI và BD là đường cao với H là trực tâm ∆ABC. Vì BE⊥CA và MA nênBE⊥(MAC)⇒BE⊥MC (1)BD là đường caoMBC nên BD⊥MC (2)Từ (1) và (2) suy ra MC⊥(BDE)⇒OH⊥MC (3)Vì BC⊥MI và MA nên BC⊥(MAI)⇒BC⊥OH (4)Từ (3) và (4) suy ra OH⊥(MBC)⇒HI⊥OH.Vậy H nhìn đoạn cố định OI dưới một góc vuông ⇔Quỹ tích H là đường tròn nằm trong mặt phẳng (MAI) có đường kính OI (trừhai điểm O và I) b) Tứ diện OHBC có đáy OBC cố định nên thể tích lớn nhất khi H ở vịtrí “cao nhất” so với đáy OBC.Xét∆OHI vuông khi gócABC=045.Hay∆OHI vuông cânMAI⇒cân⇒AM =AIVậy khi AM =AI thì thể tích tứ diện OHBC lớn nhất.Bài toán 2: Cho tam giác đều OAB có cạnh bằng a > 0. Trên đường thẳng d điqua O và vuông góc với mp (OAB) lấy điểm M với OM = x. Gọi E, F lần lượtlà các hình chiếu vuông góc của A lên MB, OB. Trên đoạn thẳng EF cắt d tại N.a)Chứng minhAN BM⊥b)Xác định x để thể tích tứ diện ABMN là nhỏ nhất.(Đại học Tổng hợp TP.HCM-1995)Hướng dẫn giảixNOFEMAB