Download.vn Học tập Lớp 12

Bạn đang đọc: Bài toán cực trị số phức

Bài toán cực trị số phức Giải bài toán cực trị số phức bằng phương pháp hình học

Giới thiệu Tải về Bình luận

• 1

Mua tài khoản Download Pro để trải nghiệm website Download.vn KHÔNG quảng cáo & tải File cực nhanh chỉ từ 79.000đ. Tìm hiểu thêm Mua ngay

Bài toán cực trị số phức là một trong những bài toán khá thú vị trong chương trình Toán lớp 12 và cũng là một trong những dạng toán khó dành cho học sinh.

Hiểu rõ được điều đó, Download.vn xin giới thiệu đến các bạn Bài toán cực trị số phức để các bạn dễ dàng hình dung và nắm bắt được kiến thức trọng tâm. Sau đây là nội dung chi tiết, mời bạn đọc cùng tham khảo và tải tài liệu tại đây.

Bài toán cực trị số phức

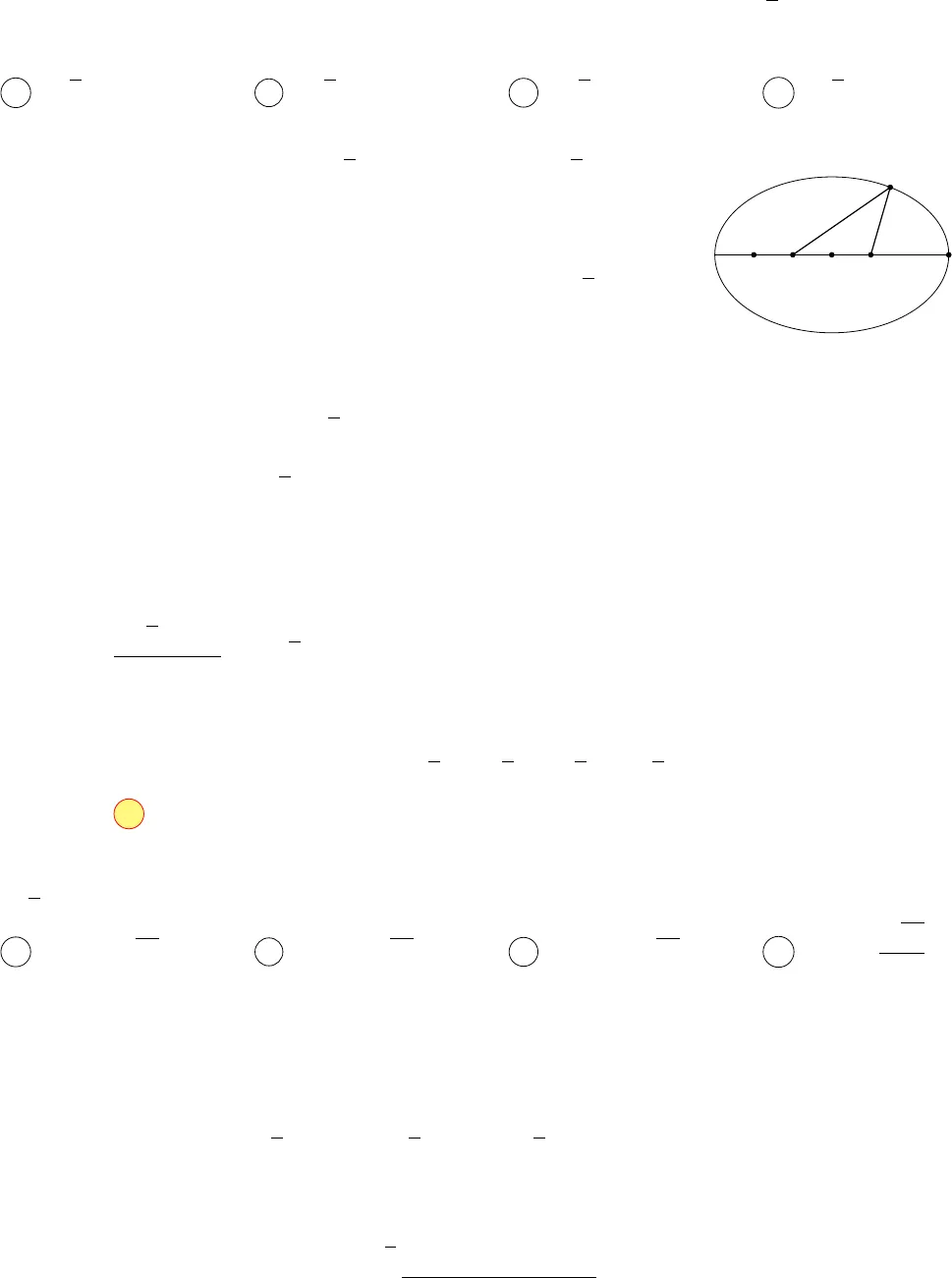1CỰC TRỊ SỐ PHỨC VÀ HÌNH HỌCCâu 1. Cho số phức z thỏa mãn điều kiện |z − 1 − i| + |z + 1 + 3i| = 6√5. Giá trị lớn nhất của|z −2 −3i| làA 5√5. B 2√5. C 6√5. D 4√5.Hướng dẫn giảiTa có |z −1 − i| + |z + 1 + 3i| = 6√5 ⇔ MA + MB = 6√5 với M(x; y)biểu diễn số phức z = x + yi, A(1; 1) biểu diễn số phức 1 + i, B(−1; −3)biểu diễn số phức −1 −3i.Khi đó điểm M nằm trên elip tâm I có độ dài trục lớn 6√5 và A, B làhai tiêu điểm.ABCIM0M• |z −2 −3i| = MC với C(2; 3) biểu diễn số phức 2 + 3i.•# »AB = (−2; −4) ⇒ AB = 2√5.•# »A C = (1; 2) ⇒ AC =√5.• Vì# »AB = −2# »A C nên# »AB,# »A C ngược hướng và AB = 2AC.Gọi M0là điểm nằm trên elip sao cho A, B, M0thẳng hàng và M0khác phía A so với B.Ta có BM0=6√5 − AB2= 2√5.Ta thấy MC ≤ M0C với mọi điểm M nằm trên elip.Do đó MC lớn nhất khi và chỉ khi M ≡ M0.Khi đó MC = M0C = CA + AB + BM0=√5 + 2√5 + 2√5 = 5√5.Chọn đáp án A Câu 2. Cho số phức z thỏa mãn |z + 1| + |z − 3 − 4i| = 10. Giá trị nhỏ nhất Pmincủa biểu thứcP = |z − 1 + 2i| bằngA Pmin=√17. B Pmin=√34. C Pmin= 2√10. D Pmin=√342.Hướng dẫn giảiĐặt z = x + yi, điểm biểu diễn của z là M(x; y).Khi đó |z + 1| + |z −3 −4i| = 10 ⇔ MA + MB = 10 với A(−1; 0) và B(3; 4).Suy ra M thuộc elip có độ dài trục lớn là 10 ⇒ 2a = 10 ⇒ a = 5 và hai tiêu điểm là A, B.Mà# »AB = (4; 4) ⇒ AB = 4√2 ⇒ 2c = 4√2 ⇒ c = 2√2.Ta cóP = |z −1 + 2i|=q(x −1)2+ (y −2)2= MH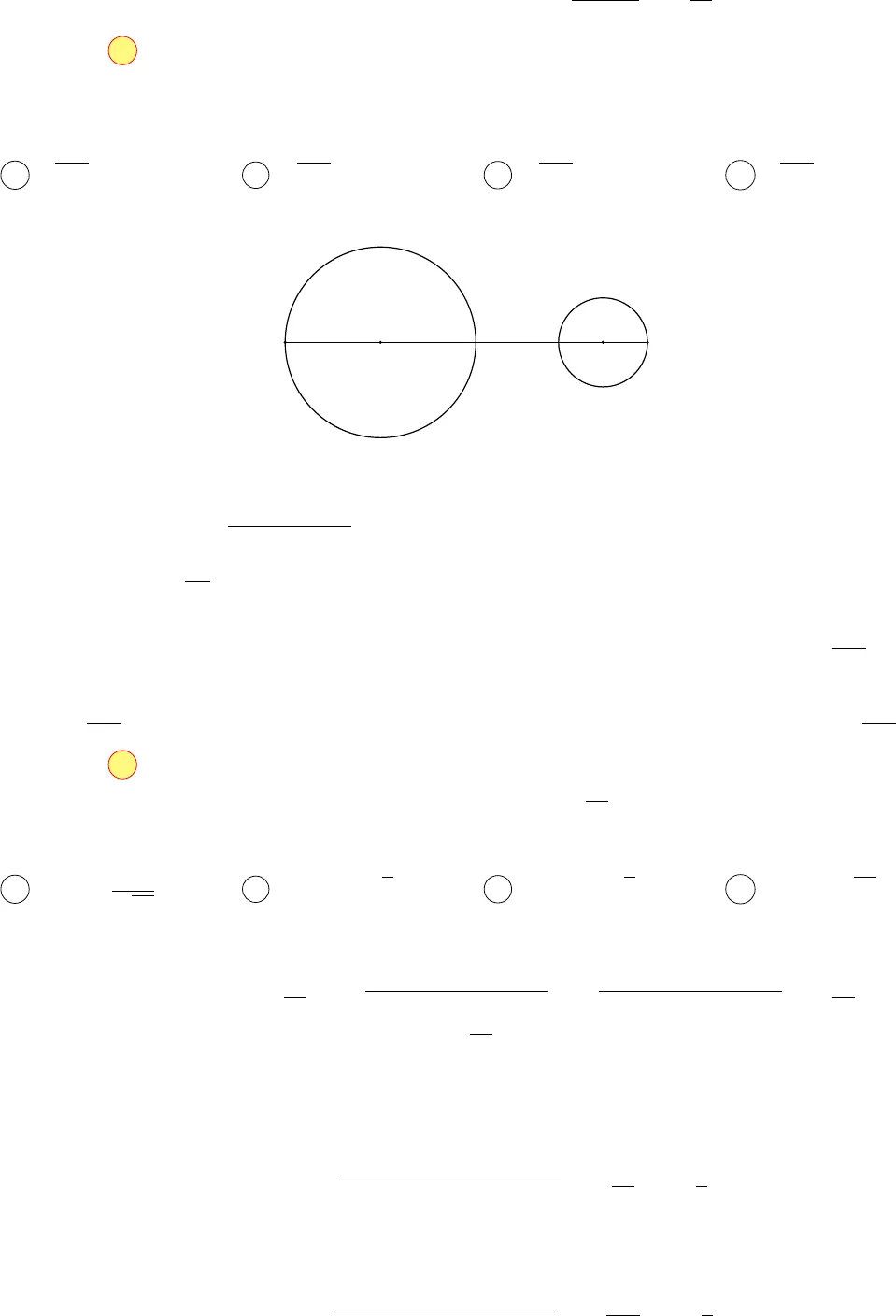2Với H(1; 2). Dễ thấy A, B, H thẳng hàng nên H thuộc đoạn AB.Do đó Pmin⇔ MH ngắn nhất khi và chỉ khi M thuộc trục nhỏ của elip.Khi đó độ dài MH bằng một nửa trục nhỏ hay MH = b =√a2−c2=√17.Chọn đáp án A Câu 3. Cho các số phức z, w thỏa mãn |z − 5 + 3i| = 3, |iw + 4 + 2i| = 2. Tìm giá trị lớn nhất củabiểu thức T = |3iz + 2w|.A√554 + 5. B√578 + 13. C√578 + 5. D√554 + 13.Hướng dẫn giảiOIA B94Ta có |z −5 + 3i| = 3 ⇔3iz −15i −93i= 3 ⇔ |3iz −9 −15i| = 9.|iw + 4 + 2i| = 2 ⇔−i2(−2w −4 + 8i)= 2 ⇔ |−2w −4 + 8i| = 4.Gọi A và B là điểm biểu diễn của 3iz và −2w, khi đó A và B lần lượt thuộc các đường tròn tâmO(9; 15) bán kính bằng 9 và đường tròn I(4; −8) bán kính bằng 4. Ta tính được OI =√554.Khi đó T = |3iz + 2w| = |3iz − (−2w)| = AB.Do IO =√554 > 4 + 9 nên hai đường tròn ngoài nhau, suy ra ABmax= AO + OI + IB =√554 + 13.Chọn đáp án D Câu 4. Xét số phức z thỏa mãn|iz −2i −2|−|z + 1 −3i|=√34. Tìm giá trị nhỏ nhất của biểu thứcP =|(1 + i)z + 2i|.A Pmin=9√17. B Pmin= 3√2. C Pmin= 4√2. D Pmin=√26.Hướng dẫn giảiGiả sử số phức z có dạng z = a + bi, z có biểu diễn hình học là điểm M(a; b). Khi đó|iz −2i −2|−|z + 1 −3i|=√34 ⇔q(b + 2)2+ (a −2)2−q(a + 1)2+ (b −3)2=√34. (1)Gọi điểm A(2; −2), B(−1; 3) khi đó ta có AB =√34. Kết hợp với (1) ta suy ra MA − MB = AB. ⇒Điểm M trùng với điểm B hoặc B là trung điểm của MA. Ta xét hai trường hợp sau:• TH1: M trùng B ⇒ M (−1; 3). Suy raP =q(a − b)2+ (a + b + 2)2=√32 = 4√2.• TH2: B là trung điểm của MA ⇒ M(−4; 8). Suy raP =q(a − b)2+ (a + b + 2)2=√180 = 6√5.3Suy ra, min P = 4√2.Chọn đáp án C Câu 5. Cho số phức z thỏa mãnz −2iz + 3 −i= 1. Giá trị nhỏ nhất của |z + 3 −2i| bằngA2√105. B 2√10. C√10. D√105.Hướng dẫn giảiGọi z = x + yi với x, y ∈ R.z −2iz + 3 −i= 1 ⇔ |z −2i| = |z + 3 − i| ⇔|x + (y −2)i|=|(x + 3) + (y − 1)i|⇔ 3x + y + 3 = 0.Vậy tập hợp các điểm biểu diễn số phức z là đường thẳng d : 3x + y + 3 = 0.Ta có |z + 3 −2i| = |z − (−3 + 2i)|, với M0(−3; 2).|z + 3 −2i| đạt giá trị nhỏ nhất bằng d(M0, d) =|−9 + 2 + 3|√9 + 1=4√10=2√105.Chọn đáp án A Câu 6. Cho các số phức z, w thỏa mãn |z| =√5, w = (4 − 3i)z + 1 − 2i. Giá trị nhỏ nhất của |w|làA 3√5. B 4√5. C 5√5. D 6√5.Hướng dẫn giảiTheo giả thiết ta có w = (4 − 3i)z + 1 − 2i ⇒ z =w −1 + 2i4 −3i.Nên |z| =√5 ⇔w −1 + 2i4 −3i=√5 ⇔|w −1 + 2i|= 5√5.Vậy, tập hợp điểm biểu diễn số phức w là đường tròn I(1; −2) và bán kính R = 5√5.Ta có OI =p12+ (−2)2=√5 R.Do đó min |w| = R −OI = 5√5 −√5 = 4√5.Chọn đáp án B Câu 7. Cho số phức z thỏa mãn |z −3 + 4i| = 2. Mô-đun lớn nhất của z bằngA 7. B 8. C 5. D 3.Hướng dẫn giảiTập hợp các điểm biểu diễn cho số phức z thỏa |z −3 + 4i| = 2 là đường tròn có tâm I(3; −4) và bánkính bằng R = 2. Suy ra max |z| = IO + R = 7.Chọn đáp án A Câu 8. Cho số phức z thỏa mãn |z − 2 − 3i| + |z − 5 + 2i| =√34. Gọi M, m lần lượt là giá trị lớnnhất và giá trị nhỏ nhất của biểu thức |z + 1 + 2i|. Khi đó tổng M + m bằngA30√34+√34. B30√34+ 5. C√34 + 6. D30√34+ 6.Hướng dẫn giải