Download.vn Học tập Lớp 12

Bạn đang đọc: Bài toán khoảng cách trong hình học không gian

Bài toán khoảng cách trong hình học không gian Tài liệu ôn tập môn Toán lớp 12

Giới thiệu Tải về Bình luận

• 1

Mua tài khoản Download Pro để trải nghiệm website Download.vn KHÔNG quảng cáo & tải File cực nhanh chỉ từ 79.000đ. Tìm hiểu thêm Mua ngay

Bài toán khoảng cách trong hình học không gian gồm 14 trang hướng dẫn phương pháp xác định và tính khoảng cách trong không gian và các ví dụ áp dụng có hướng dẫn giải.

Hy vọng đây sẽ là tài liệu hữu ích dành cho các bạn học sinh lớp 12 có thêm nhiều tài liệu học tập, củng cố kiến thức để đạt được kết quả cao trong các bài kiểm tra, bài thi THPT Quốc gia 2020 sắp tới. Đồng thời đem đến cho các thầy cô có thêm nhiều tài liệu giảng dạy. Ngoài ra các bạn tham khảo thêm một số tài liệu như: bài tập trắc nghiệm thể tích khối lăng trụ đều, bài tập trắc nghiệm sự đồng biến và nghịch biến của hàm số. Nội dung chi tiết mời các bạn cùng theo dõi bài viết dưới đây.

Bài toán khoảng cách trong hình học không gian

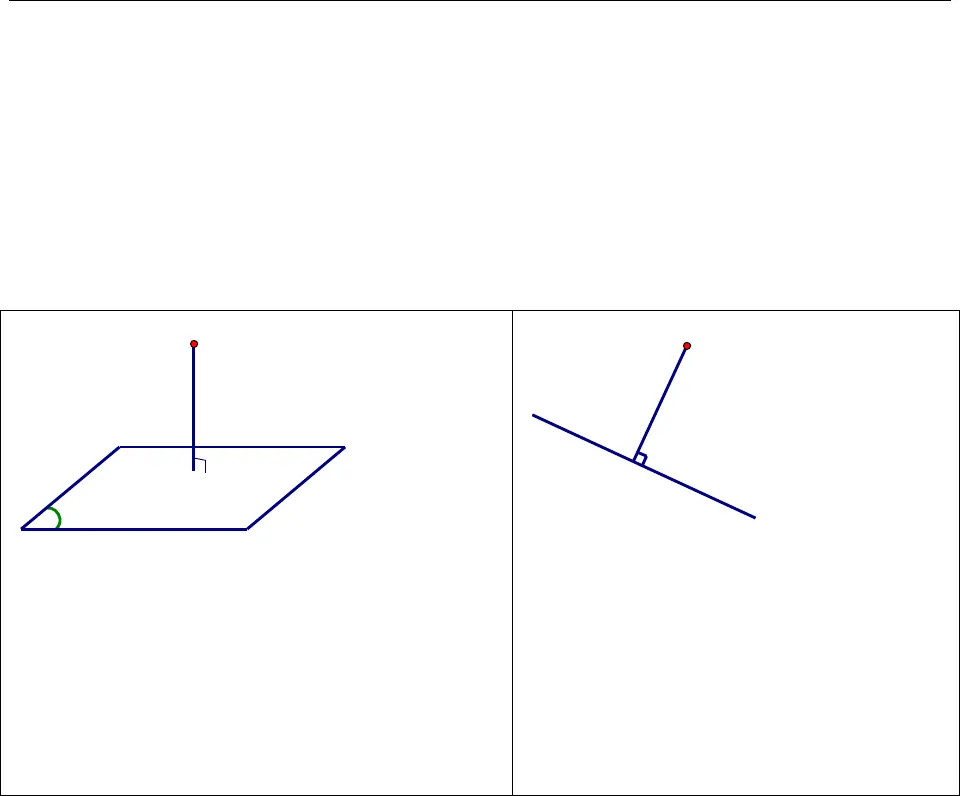BÀI GIẢNG ÔN THI VÀO ĐẠI HỌC BÀI TOÁN KHOẢNG CÁCH TRONG HÌNH HỌC KHÔNG GIANTHS. PHẠM HỒNG PHONG – GV TRƯỜNG ĐH XÂY DỰNG DĐ: 0983070744 website: violet.vn/phphong84 1BÀI TOÁN KHOẢNG CÁCH TRONG HÌNH HỌC KHÔNG GIANLoại 1. Khoảng cách từ điểm đến mặt phẳng, một đường thẳng A. Tóm tắt lý thuyết1. Định nghĩa: Khoảng cách từ một điểm đến mặt phẳng (hoặc đường thẳng) bằng khoảng cách từ điểm đó tới hình chiếu vuông góc của nó lên mặt phẳng (hoặc đường thẳng). Khoảng cách từ điểmMtới mặt phẳngPđượcký hiệu là d M; P.Hlà hình chiếu vuông góc củaMlênPthìd M; P MHKhoảng cách từ điểmMtới đường thẳng được ký hiệu làd M;.Hlà hình chiếu vuông góc củaMlênthìd M; MH . 2. Bài toán cơ bản: Nhiều bài toán tính khoảng cách từ điểm tới mặt phẳng, từ điểm tới đường thẳng có thể quy về bài toán cơ bản sau Bài toán: Cho hình chóp S.ABCcóSAvuông góc với đáy. Tính khoảng cách từ điểm Ađếnmặt phẳngSBCvà khoảng cách từ điểm Sđến đường thẳngBC.Cách giải HPMΔMH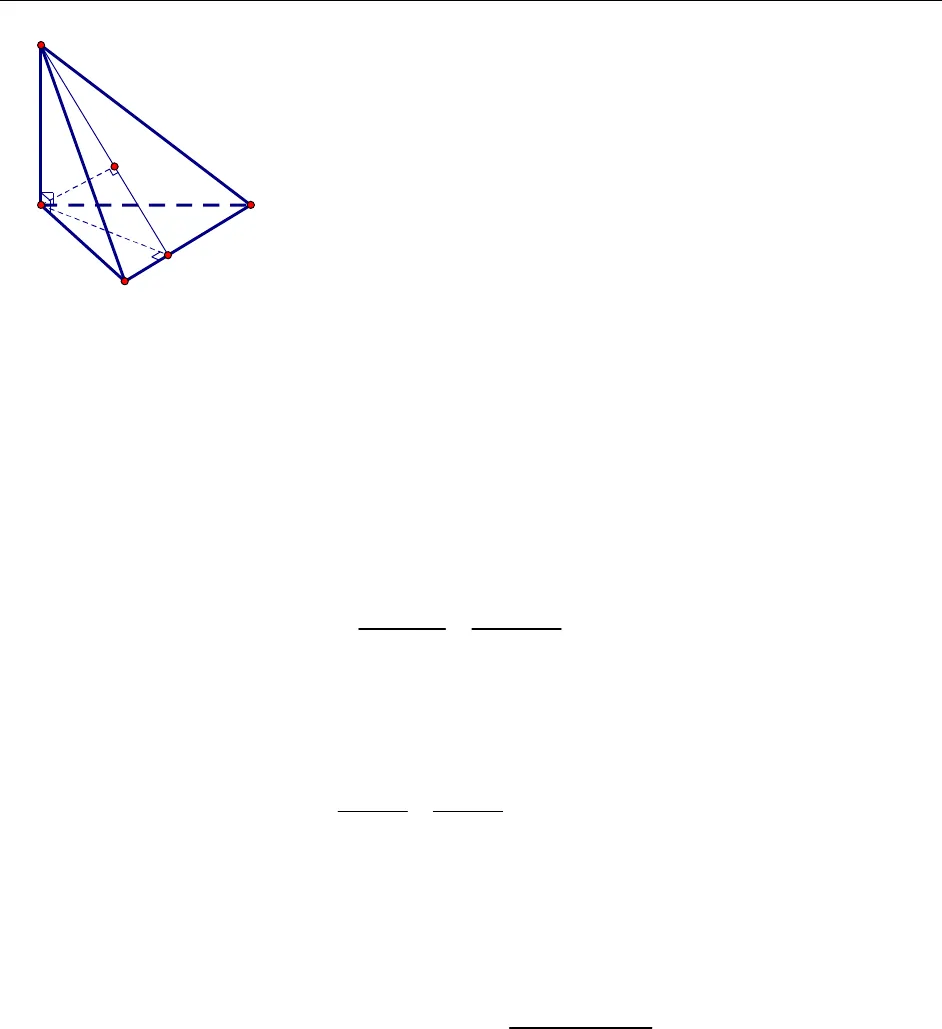BÀI GIẢNG ÔN THI VÀO ĐẠI HỌC BÀI TOÁN KHOẢNG CÁCH TRONG HÌNH HỌC KHÔNG GIANTHS. PHẠM HỒNG PHONG – GV TRƯỜNG ĐH XÂY DỰNG DĐ: 0983070744 website: violet.vn/phphong84 2GọiDlà chân đường vuông góc hạ từ AxuốngBC,Hlà chânđường vuông góc hạ từ AxuốngSD. Ta có+)SA ABCBC SA, lại cóBC AD(do dựng)BC SADSD BCd S;BC SD.+) Từ chứng minh trên, đã có BC SADAH BC, lạicóAH SD(do vẽ) AH SBCd A; SBC AH.3. Một số lưu ý* Về cách tính khoảng cách một cách gián tiếp +)MN Pd M; P d N; P.+)   M,N QQ Pd M; P d N; P.+)MN P I d M; P d M; QMI NI.Trường hợp đặc biệt: Ilà trung điểm của MNd M; P d N; P.+)MNd M; d N;  .+)MN I d M; d M;MI NI .Trường hợp đặc biệt: Ilà trung điểm của MNd M; d N;  .* Về cách sử dụng thể tích để tính khoảng cách từ điểm đến mặt phẳng: Cho hình chóp 1 2 nS.A A …A. Ta có 3VS.A A ...A1 2 n1 2 nSA A ...A1 2 nd S, A A ...A  .* Khoảng cách từ một đường thẳng tới mặt phẳng song song với nó: Cho P,Mlà một điểm bất kỳ trên . Khi đó d ; P d M; P .* Khoảng cách giữa hai mặt phẳng song song: Cho P Q,Mlà một điểm bất kỳ trên P. Khi đó SACBDH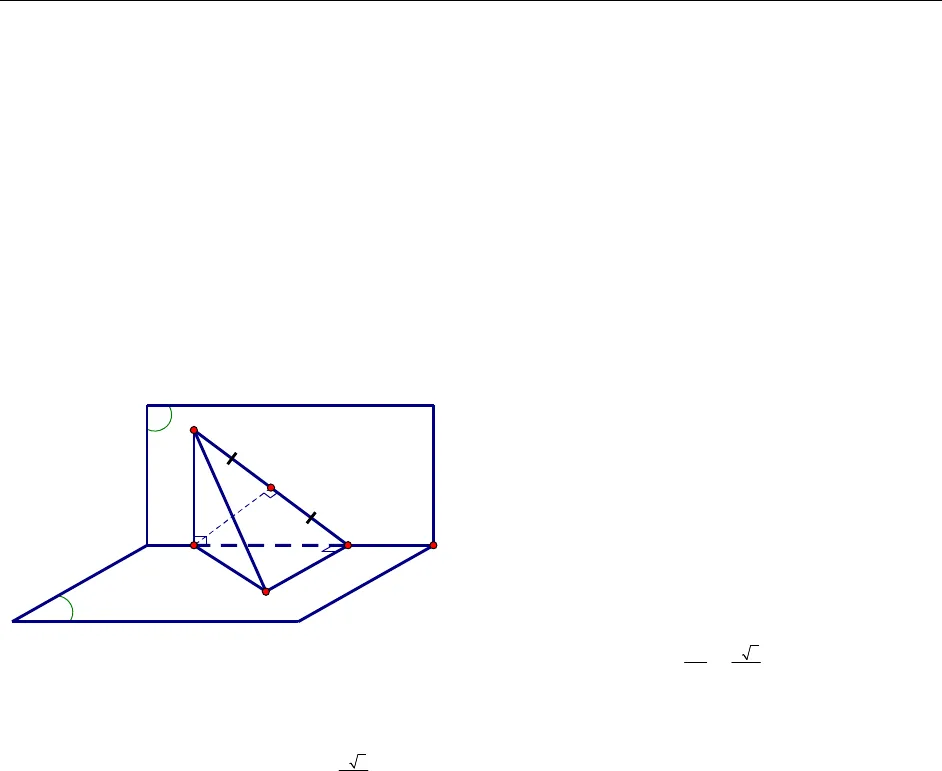BÀI GIẢNG ÔN THI VÀO ĐẠI HỌC BÀI TOÁN KHOẢNG CÁCH TRONG HÌNH HỌC KHÔNG GIANTHS. PHẠM HỒNG PHONG – GV TRƯỜNG ĐH XÂY DỰNG DĐ: 0983070744 website: violet.vn/phphong84 3d P ; Q d M; Q.B. Một số ví dụVí dụ 1. [ĐHD03] Cho hai mặt phẳng PvàQvuông góc với nhau, cắt nhau theo giaotuyến . LấyA,Bthuộcvà đặtAB a. LấyC,Dlần lượt thuộc PvàQsao choAC,BDvuông góc vớivàAC BD a . Tính khoảng cách từAđến mặt phẳng phẳng BCD.Giải Ta cóP Q , P Q  ,AC P , AC AC Q BD AC. Lại cóBD ABBD ABC 1.GọiHlà chân đường vuông góc hạ từ AxuốngBC. VìABCvuông cân tạiAnênAH BCvà22 2aBCAH   . Từ1suy raAH BDAH BCD . Do đó Hlà chân đường vuông góc hạ từ AlênBCD22;ad A BCD AH  . Ví dụ 2. [ĐHD12] Cho hình hộp đứng . ‘ ‘ ‘ ‘ABCD A B C Dcó đáy là hình vuông, tam giác ‘A ACvuông cân, ‘A C a. Tính khoảng cách từ điểm Ađến mặt phẳng ’BCDtheoa.Giải QPΔaaaHABCD