Download.vn Học tập Lớp 12

Bạn đang đọc: Bài toán thực tế và bài toán tối ưu Min – Max

Bài toán thực tế và bài toán tối ưu Min – Max Tài liệu ôn tập môn Toán lớp 12

Giới thiệu Tải về Bình luận

• 1

Mua tài khoản Download Pro để trải nghiệm website Download.vn KHÔNG quảng cáo & tải File cực nhanh chỉ từ 79.000đ. Tìm hiểu thêm Mua ngay

Bài toán thực tế và bài toán tối ưu Min – Max là tài liệu hữu ích mà Download.vn muốn giới thiệu đến quý thầy cô giáo cùng các bạn lớp 12 tham khảo.

Tài liệu gồm 23 trang tuyển chọn các bài toán thực tế và bài toán tối ưu min – max. Nội dung tài liệu bao gồm 3 phần: bài toán thực tế tối ưu, các bài toán thực tế liên quan đến tích phân; Bài toán thực tế liên quan đến mũ và lôgarit; Bài tập rèn luyện trích từ đề thi THPT Quốc gia. Sau đây là nội dung chi tiết mời các bạn cùng tham khảo và tải tài liệu tại đây.

Bài toán thực tế và bài toán tối ưu Min – Max

Giáo viên sưu tầm và biên soạn: Lê Viết NhơnFacebook: www.facebook.com/viet.nhon Trang 1 BÀI TOÁN THỰC TẾBÀI TOÁN TỐI ƯU MIN – MAX Tài liệu có tham khảo nguồn: 1) Bài toán tối ưu Min_max của thầy Lê Bá Bảo. 2) Tuyển chọn các bài toán thực tế của thầy Nguyễn Văn Rin. 3) Một số bài toán của thầy Hồ Hà ĐặngA. BÀI TẬP SÁCH GIÁO KHOAPHẦN 1. BÀI TOÁN THỰC TẾ_TỐI ƯU Ví dụ 1. (SGK 12 CB) Trong số các hình chữ nhật có cùng chu vi 16cm, hãy tìm hình chữnhật có diện tích lớn nhất.Hướng dẫn giảiHình vuông có cạnh bằng4cmlà hình có diện tích lớn nhất và2max 16S cmVí dụ 2. (SGK 12 CB) Trong tất cả các hình chữ nhật có diện tích 248m, hãy xác định hìnhchữ nhật có chu vi nhỏ nhất.Hướng dẫn giải:Hình vuông có cạnh bằng4 3mlà hình có chu vi nhỏ nhất vàmin 16 3 .P mVí dụ 3. (SGK BT 12 CB) Trong các hình trụ nội tiếp hình cầu bán kính ,Rhãy tìm hình trụ cóthể tích lớn nhất.Hướng dẫn giải:Kí hiệu chiều cao, bán kính đáy và thể tích của hình trụ nội tiếp hình cầu lần lượt là,h rvà.VKhi đó:2.V h rVì2 2 32 2 2 2.4 4 4h h hr R V h R hR                Ví dụ trở thành tìm giá trị lớn nhất của hàm số   32, 0; 2 .4hV h hR h R     Ta có: 223 2′ 0 .43h RV h R h       Bảng biến thiên:h023R2R’V0V0343 3R 0Từ BBT, suy ra 30;22 4max .3 3 3RR RV V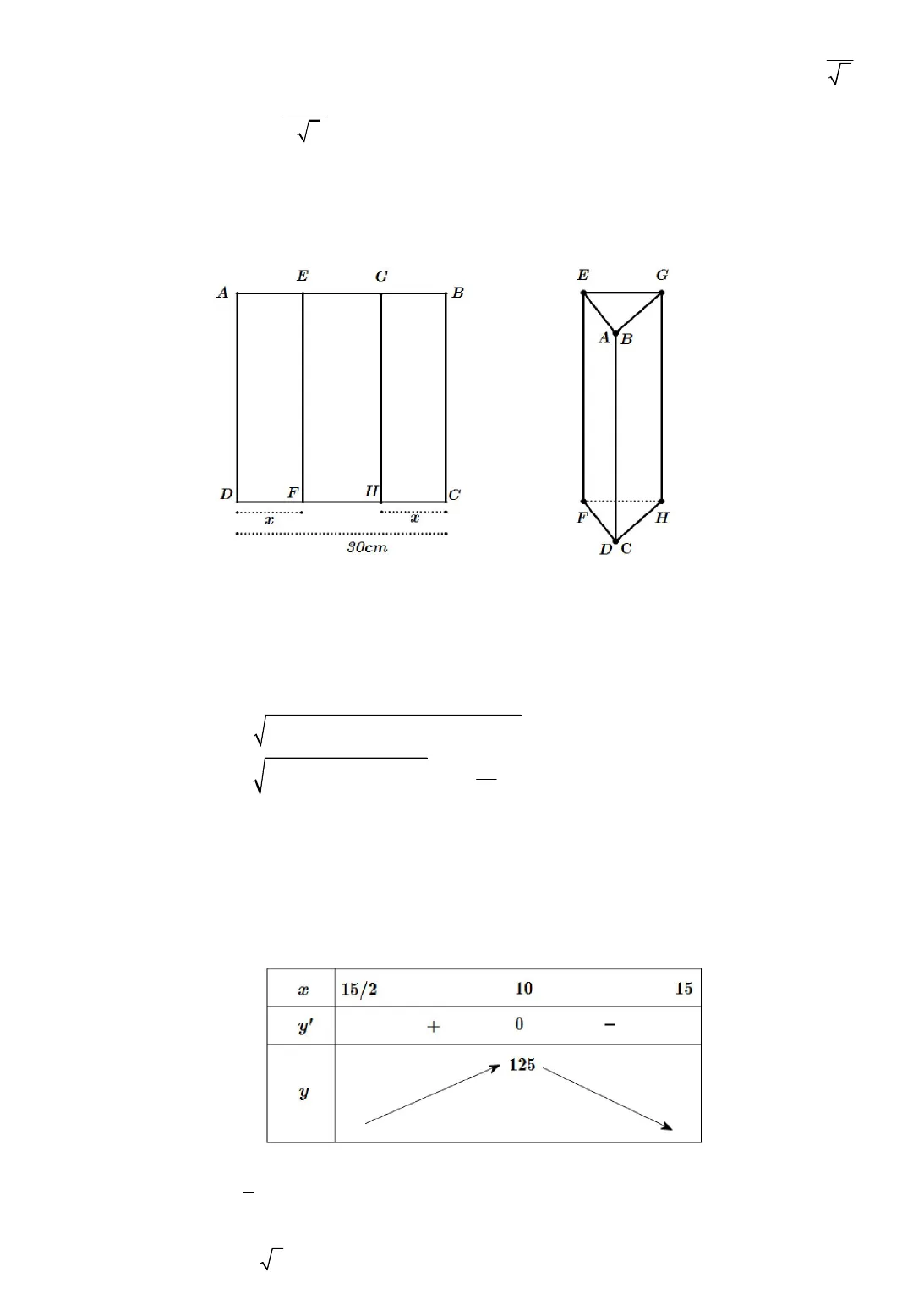    Giáo viên sưu tầm và biên soạn: Lê Viết NhơnFacebook: www.facebook.com/viet.nhon Trang 2 Vậy hình trụ nội tiếp hình cầu bán kínhRcó thể tích lớn nhất khi chiều cao của nó bằng23R.Khi đó, thể tích khối trụ là34.3 3RVí dụ 4. (Team 12 Huế) Một tấm kẽm hình vuông ABCDcó cạnh bằng30 .cmNgười ta gậptấm kẽm theo hai cạnhEFvàGHcho đến khiADvàBCtrùng nhau như hình vẽ dưới đây đểđược một hình lăng trụ khuyết hai đáy. Giá trị củaxđể thể tích khối lăng trụ lớn nhất làA.5 .x cmB.9 .x cmC.8 .x cmD.10 .x cm Hướng dẫn giải:Ta có:Δ, 30 2 15.DHFDF CH x FH x p    Thể tích khối lăng trụ như hình vẽ là. 30 15 15 15 15 30 2FDHV S EF x x x     21530 15 15 2 15 , ;152x x x      Xét hàm số215 2 15f x x x  2′ 2 15 2 15 2 15 2 15 3 30fx xx x xx        10′ 0 .15xf xx  Bảng biến thiên: Dựa vào BBT,15;152max 125f x  khi10.x Do đó thể tích khối lăng trụ như hình vẽ lớn nhất khi10 .x cm Khi đó3max750 3 .V cm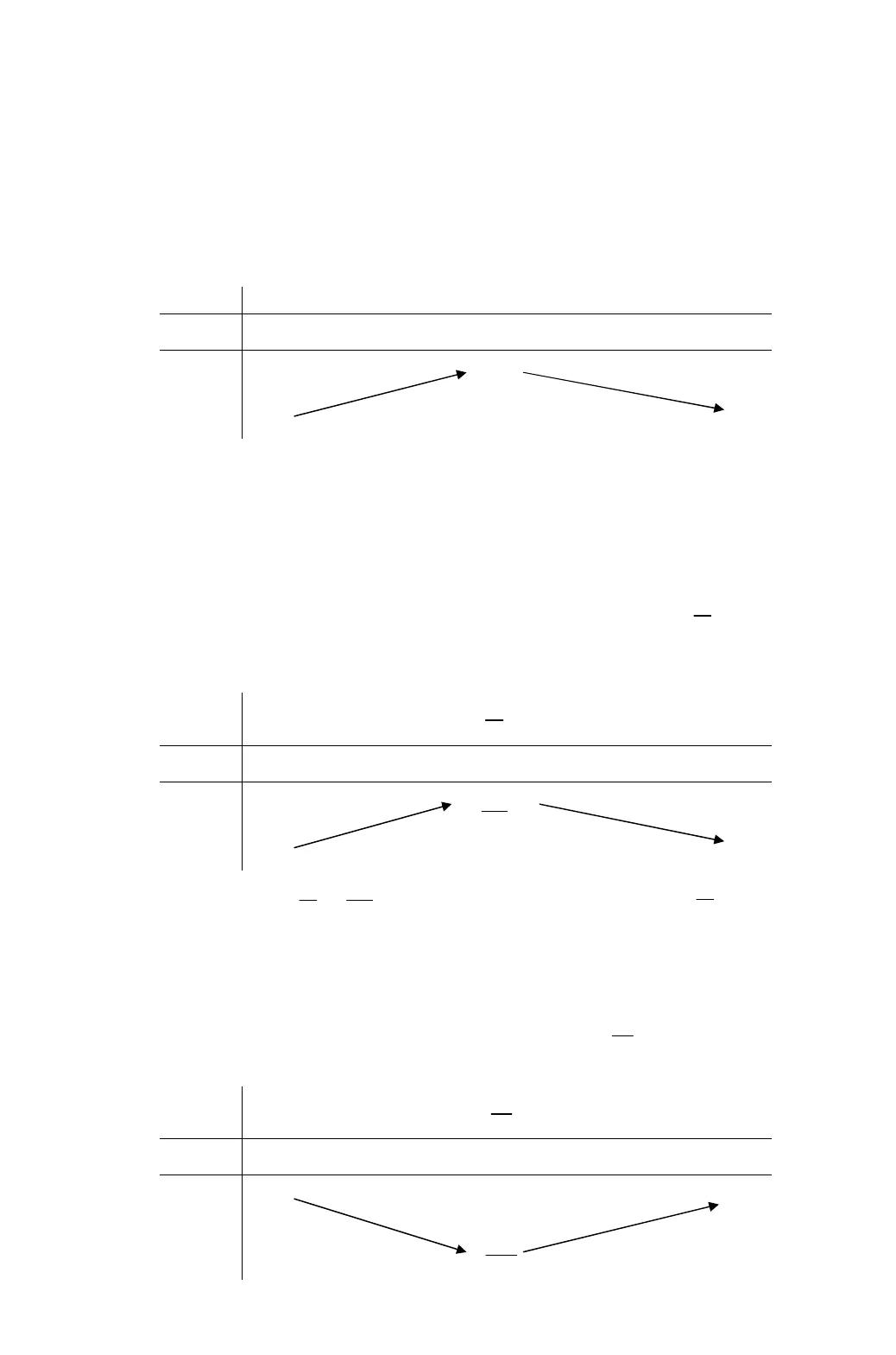Giáo viên sưu tầm và biên soạn: Lê Viết NhơnFacebook: www.facebook.com/viet.nhon Trang 3 Lựa chọn đáp án D.Ví dụ 5. (SGK BT 12 CB) Một chất điểm chuyển động theo quy luật 2 36 .s t t t Tính thờiđiểmt(giây) tại đó vận tốc/v m scủa chuyển động đạt giá trị lớn nhất.Hướng dẫn giải:Theo giả thiết:2 36 , 0; .s t t t t   Vận tốc của chuyển động là2′ 12 3 .vtst tt  Ta có:’ 12 6 0 2.v t t t    Bảng biến thiên:t02’v t0v t12 Dựa vào BBT, ta có 0;max 2 12 /v t v m s . Vậy vận tốc đạt giá trị lớn nhất khi2 .t sVí dụ 6. (SGK BT 12 CB) Cho số dương m. Hãy phân tíchmthành tổng của hai số dương saocho tích của chúng là lớn nhất.Hướng dẫn giải:Cho0.mĐặtxlà số thứ nhất,0 ,x m số thứ hai là.m xXét tích, 0;P x x m x x m  . Ta có: ’ 2 0 .2mP x x m x     Bảng biến thiên:x02mm’P x0P x24m Từ BBT, ta có  20;max .2 4mm mP x P    Vậy phân tíchmthành tổng hai số.2mVí dụ 7. (SGK BT 12 CB) Tìm hai số có hiệu là 13sao cho tích của chúng là bé nhất.Hướng dẫn giải:Gọi một trong hai số phải tìm là,xta có số kia là13.xXét tích13P x x x . Ta có: 13′ 2 13 0 .2P x x x     Bảng biến thiên:x132’P x0P x 1694 