Bộ công thức Toán ôn thi THPT Quốc gia dưới đây là những công thức quan trọng các em lớp 12 cần ghi nhớ để vận dụng tính toán nhanh nhất các bài toán thi THPT Quốc gia và cho ra kết quả chính xác.
Bạn đang đọc: Bộ công thức Toán ôn thi THPT Quốc gia
Trong đề thi THPT Quốc gia môn Toán thì số lượng công thức cần ghi nhớ là không hề nhỏ. Đối với các bài thi trắc nghiệm, điều cần thiết là các em học sinh cần nắm kiến thức rộng và có phương pháp giải nhanh hiệu quả để có thể ghi điểm nhiều nhất. Vì thế dưới đây là trọn bộ công thức Toán ôn thi THPT Quốc gia mời các bạn theo dõi. Bên cạnh công thức giải nhanh Toán 12 các bạn xem thêm công thức tính thể tích khối tròn xoay.
Công thức Toán thi THPT Quốc gia 2023
Phần 1: Công thức Toán học phần Đại số
- Tam thức bậc 2
- Bất đẳng thức Cauchy
- Cấp số cộng
- Cấp số nhân
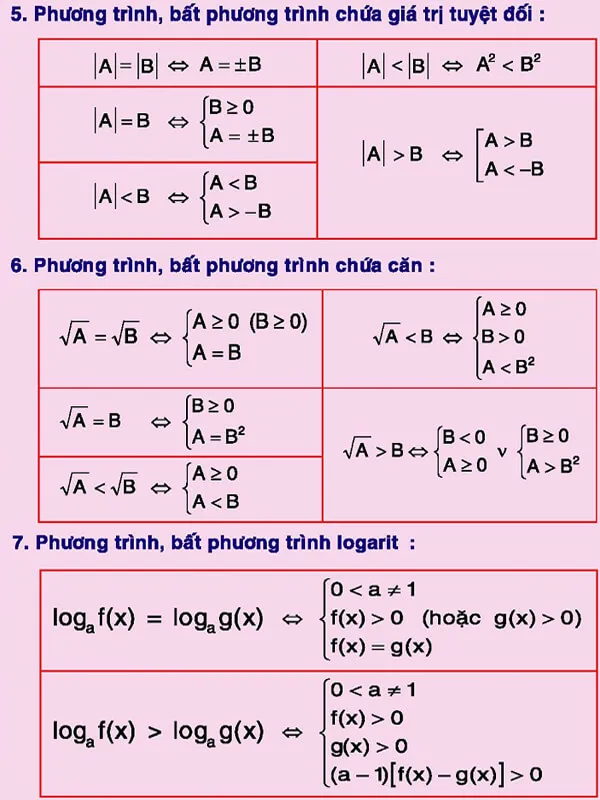
- Phương trình, bất phương trình chứa giá trị tuyệt đối
- Phương trình, bất phương trình chứa căn
- Phương trình, bất phương trình logarit
- Phương trình, bất phương trình mũ
- Lũy thừa
- Logarit



Phần II. Công thức phần Lượng giác
Bao gồm 3 chuyên đề lớn
- Công thức lượng giác
- Phương trình lượng giác
- Hệ thức lượng trong tam giác

3. Công thức cộng lượng giác
1. sin (a ± b) = sin a.cos b ± cos a.sin b
2. cos (a + b) = cos a.cos b – sin a.sin b
3. cos (a – b) = cos a.cos b + sin a.sin b
Mẹo nhớ công thức cộng: Sin thì sin cos cos sin, cos thì cos cos sin sin dấu trừ. Tan thì tan nọ tan kia chia cho mẫu số 1 trừ tan tan.
4. Công thức các cung liên kết trên đường tròn lượng giác
|
Góc đối nhau ( cos đối) |
Góc bù nhau (sin bù) |
Góc phụ nhau (Phụ chéo) |
Góc hơn kém (Khác pi tan) |
| cos (-α) = cos α | sin (π – α) = sin α | sin (π/2 – α)= cos α | sin (π + α) = – sin α |
| sin (-α) = -sin α | cos (π – α) = – cos α | cos (π/2 – α) = sinα | cos (π + α) = – cosα |
| tan (-α) = – tan α | tan ( π – α) = – tan α | tan (π/2 – α) = cot α | tan (π + α) = tanα |
| cot (-α) = -cot α | cot (π – α) = – cot α | cot (π/2 – α) = tan α | cot (π + α) = cotα |
Cung hơn kém π / 2
- cos(π/2 + x) = – sinx
- sin(π/2 + x) = cosx
Thơ nhớ cung đặc biệt
Cos đối, sin bù, phụ chéo, khác pi tan.
Cosin của 2 góc đối thì bằng nhau.
Sin của 2 góc bù nhau cũng bằng nhau.
Phụ chéo là 2 góc phụ nhau thì sin góc này bằng cos góc kia.
Tan góc này bằng Cot góc kia.
Tan của 2 góc hơn kém pi cũng bằng nhau.
5. Công thức nhân
a. Công thức nhân đôi
- sin2a = 2sina.cosa
- cos2a = cos2a – sin2a = 2cos2a – 1 = 1 – 2sin2a
- tan2a =
Thơ:
Sin gấp đôi thì bằng 2 lần sin cos
Cos gấp đôi bằng bình cos trừ bình sin, bằng luôn hai cos bình trừ đi 1, cũng bằng một trừ hai sin bình mà thôi.
Tang gấp đôi, ta lấy 2 tang chia đi một trừ bình tang ra liền.
b. Công thức nhân ba
- sin3a = 3sina – 4sin3a
- cos3a = 4cos3a – 3cosa
- tan3a =
Thơ:
Nhân 3 một gốc bất kỳ.
Sin thì ba bốn, Cos thì bốn ba.
Dấu trừ đặt giữa hai ta, lập phường thì bốn chỗ, thế là ra ngay.
6. Công thức hạ bậc
7. Biến đổi tổng thành tích
Thơ nhớ:
Sin tổng lập tổng sin cô.
Cô tổng lập hiệu đôi cô đôi chàng.
Tan tổng thì lập tổng hai tan.
Một trừ tan tích mẫu mang thương sầu.
Gặp hiệu ta chớ phải lo.
Đổi trừ thành cộng ghi sâu trong lòng.
8. Biến đổi tích thành tổng
Thơ:
Cos cos thì nữa cos cộng cộng cos trừ.
Sin sin thì trừ nữa cos cộng trừ cos trừ.
Sin cos thi nữa sin cộng cộng sin trừ.
9. Nghiệm phương trình lượng giác
| Kiến thức cơ bản |
Trường hợp đặc biệt |
|
|
|
10. Dấu của các giá trị lượng giác
| Góc phần tư số | I | II | III | IV |
| Giá trị lượng giác | ||||
| sin x | + | + | – | – |
| cos x | + | – | – | + |
| tan x | + | – | + | – |
| cot x | + | – | + | – |
11. Bảng giá trị lượng giác một số góc đặc biệt
|
|
|
|
|
|
|
|
|
|
|
|
|
| 0 | 0 | -1 | 0 | ||||||||
| 1 | 0 | -1 | 0 | 1 | |||||||
| 0 | 1 | || | -1 | 0 | || | 0 | |||||
| || | 1 | 0 | -1 | || | 0 | || |
12. Công thức lượng giác bổ sung
- tan a + cot a =
- cot a – tan a = 2cot 2a
- sin4a + cos4a = 1 –
sin2 2a =
cos4a +
- sin6a + cos6a = 1 –
sin2 2a =
cos4a +
Biểu diễn công thức theo
|
|
|

Xem thêm: Bảng công thức lượng giác cần nhớ
Phần III. Đạo hàm – Tích phân – Hình học – Nhị thức Newton
1. Đạo hàm
2. Bảng các nguyên hàm
3. Diện tích hình phẳng – Thể tích vật thể tròn xoay
4. Phương pháp tọa độ trong mặt phẳng
5. Phương pháp tọa độ trong không gian
6. Nhị thức Newton
…………………..
Mời các bạn tải File tài liệu về để xem thêm nội dung chi tiết

