Download.vn Học tập Lớp 11

Bạn đang đọc: Bộ đề kiểm tra 1 tiết Chương 1 Đại số và Giải tích lớp 11 (10 đề)

Bộ đề kiểm tra 1 tiết Chương 1 Đại số và Giải tích lớp 11 (10 đề) Đề kiểm tra 45 phút Đại số lớp 11 có đáp án

Giới thiệu Tải về Bình luận

• 35

Mua tài khoản Download Pro để trải nghiệm website Download.vn KHÔNG quảng cáo & tải File cực nhanh chỉ từ 79.000đ. Tìm hiểu thêm Mua ngay

Download.vn mời quý thầy cô cùng các bạn học sinh lớp 11 cùng tham khảo tài liệu Bộ đề kiểm tra 1 tiết Chương 1 Đại số và Giải tích lớp 11 được chúng tôi đăng tải sau đây.

Đây là đề kiểm tra nhằm khảo sát, đánh giá chất lượng học sinh. Tài liệu bao gồm 10 đề kiểm tra 45 phút có đáp án chi tiết kèm theo sẽ giúp các bạn ôn tập kiến thức nhằm chuẩn bị cho bài thi cuối học kì 1 sắp tới. Đồng thời, qua đó giúp quý thầy cô đánh giá được khả năng làm bài của học sinh để ra đề thi phù hợp. Sau đây, mời quý thầy cô và các em cùng tham khảo

Bộ đề kiểm tra 1 tiết Chương 1 Đại số và Giải tích lớp 11

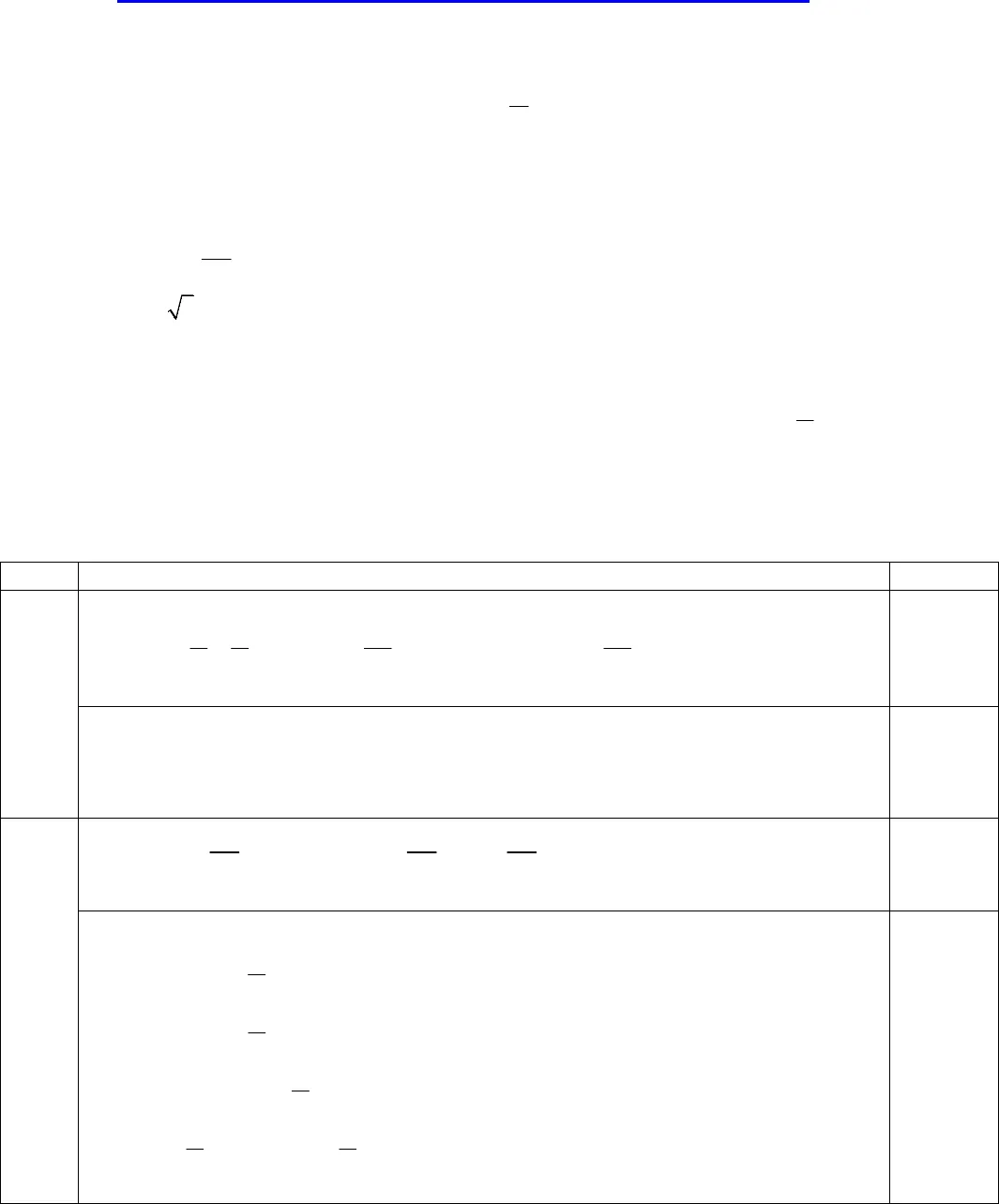BỘ ĐỀ KIỂM TRA 1 TIẾT ĐẠI SỐ &GIẢI TÍCH 11 CHƯƠNG IĐỀ SỐ 1Câu 1: (3 điểm)a) Tìm tập xác định của hàm sốtan4y x    .b) Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số1 3sin 2y x .Câu 2: (6 điểm) Giải các phương trình saua)2cot cot 07x . b)2 22sin 3sin cos cos 2x x x x  .c)sin 3 cos 4sin 2 cosx x x x . d)cos3 cos 2 9sin 4 0x x x   Câu 3: (1 điểm) Cho phương trình  21 sin cos 2 3 sin sin 1 cosx x m x x m x    (m là tham số)Tìm các giá trị thực của m để phương trình có 6 nghiệm khác nhau thuộc khoảng;22   ………….. HẾT ………….ĐÁP ÁNCÂUĐáp ánĐIỂMCâu13đa) ĐK:34 2 4x k x k        TXĐ: D =3,4k k    1.0 + 0.5b) TXĐ: D =Ta có:1 sin 2 1, 2 4,x x y x           Vậy: GTLN y = -2, GTNN y = 40.250.5+0.50.25Câu26đa)2 2 2cot cot 0 cot cot7 7 7x x x k        1.0+1.0b)2 22sin 3sin cos cos 2x x x x  (1)* cosx = 02x k  là nghiệm của (1)* cosx ≠ 02x k  . Ta có: (1) 2 22 tan 3tan 1 2 1 tanx x x    tan 14x x k      .Vậy:2x k và4x k  0.50.50.50.5c)sin 3 cos 4sin 2 cosx x x x  sin 3 cos 2 sin 3 sin 3 cos sin 2sin 3x x x x x x x      12 2sin sin 3 ( )33kxx x k Zx k          0.25+0,250.25+0,25d) Ta cócos3 cos 2 9sin 4 0x x x   3 24cos 3cos 2sin 9sin 5 0x x x x        2cos 1 4sin 2sin 1 sin 5 0x x x x       2sin 1 cos 2sin cos sin 5 0x x x x x        2sin 1 0 1sin cos 2sin cos 5 0 2xx x x x    Giải 1, ta có 2161 sin5226x kxx k    .Giải 2, đặtsin cos 2 sin4t x x x      với2t .Khi đó2 21 2sin cos 2sin cos 1t x x x x t    ;Phương trình 2trở thành2 21 5 0 4 0t t t t       phương trình vônghiệm.0.50.250,25Câu31đ          221 sin cos 2 3 sin sin 1 cos1 sin cos2 3sin 11 sin 0.cos2 2 1 sin 1 02sin sin 1 1 sin 1 sisin 2 1 sin 0sin 11sin .2sinnxxx x m x x m xx x m x x m xx m x mx m x mxxx mx                     +) Phương trìnhsin 1 22x x k   có 1 nghiệm là2thuộc;22   .+) Phương trình216sin5226x kxx k   có 2 nghiệm là5;6 6 thuộc;22   .Do đó yêu cầu bài toánsin x m có 3 nghiệm thuộc khoảng;22   1 0m   0.250.250,250,25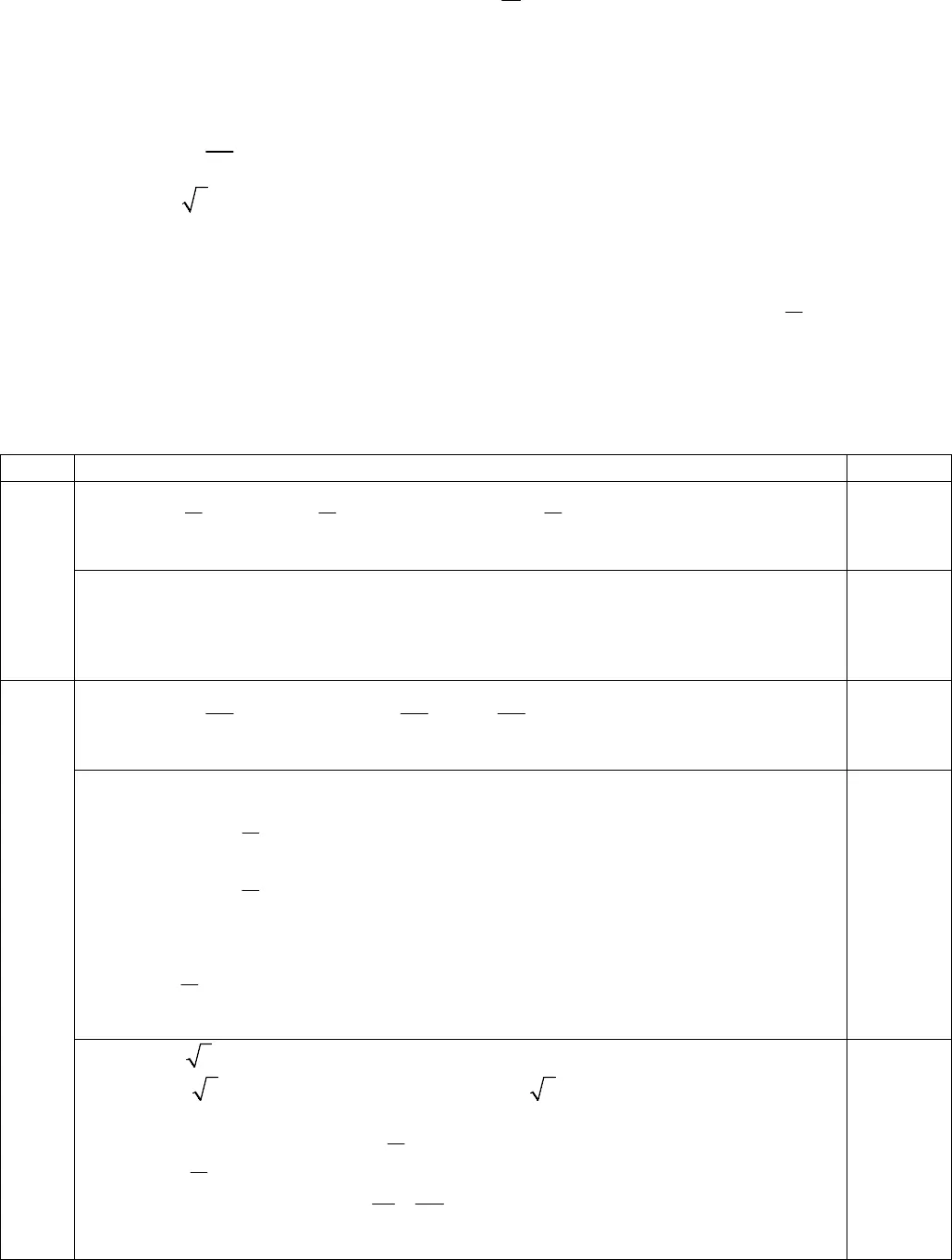ĐỀ SỐ 2Câu 1: (3 điểm)a) Tìm tập xác định của hàm sốcot4y x    .b) Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số2 3cos 2y x .Câu 2: (6 điểm) Giải các phương trình saua)3tan tan 07x . b)2 23sin 2sin cos cos 3x x x x  .c)3cos 3sin 4cos2 .cosx x x x . d)sin 3 cos 2 9cos 4 0x x x   .Câu 3: (1 điểm) Cho phương trình  21 cos cos 2 3 cos cos 1 sinx x m x x m x    (m là tham số)Tìm các giá trị thực của m để phương trình có 6 nghiệm khác nhau thuộc khoảng;22   ………….. HẾT ………….ĐÁP ÁNCÂUĐáp ánĐIỂMCâu13đa) ĐK:4 4x k x k      TXĐ: D =,4k k    1.0 + 0.5b) TXĐ: D =Ta có:1 cos 2 1, 1 5,x x y x           Vậy: GTLN y = -1, GTNN y = 50.250.5+0.50.25Câu26đa)3 3 3tan tan 0 tan tan7 7 7x x x k        1.0+1.0b)2 23sin 2sin cos cos 3x x x x  (1)* cosx = 02x k  là nghiệm của (1)* cosx ≠ 02x k  Ta có: (1) 2 23tan 2 tan 1 3 1 tanx x x     tan 2 arctan 2x x k      .Vậy:2x k và arctan 2x k  0.50.50.50.5c)3cos 3sin 4cos 2 cosx x x x  3cos 3sin 2 cos3 cos cos 3 sin 2cos3x x x x x x x      6cos cos3 ( )312 2x kx x k Zkx           0.25+0,250.25+0,25