TOP 3 Đề thi học kì 2 môn Toán 6 sách Chân trời sáng tạo năm 2023 – 2024 có đáp án, hướng dẫn chấm và bảng ma trận kèm theo, giúp thầy cô xây dựng đề thi học kì 2 cho học sinh của mình theo chương trình mới.
Bạn đang đọc: Bộ đề thi học kì 2 môn Toán 6 năm 2023 – 2024 sách Chân trời sáng tạo
Với 3 Đề thi học kì 2 môn Toán 6 Chân trời sáng tạo, các em dễ dàng luyện giải đề, nắm vững cấu trúc đề thi để đạt kết quả cao trong kỳ thi học kì 2 năm 2023 – 2024 sắp tới. Ngoài ra, có thể tham khảo thêm đề thi học kì 2 môn Công nghệ, Khoa học tự nhiên. Mời thầy cô và các em cùng theo dõi bài viết dưới đây của Download.vn:
Đề thi cuối kì 2 môn Toán 6 Chân trời sáng tạo năm 2023 – 2024
1. Đề thi học kì 2 môn Toán 6 sách Chân trời sáng tạo – Đề 1
1.1. Đề thi học kì 2 môn Toán 6
|
Trường THCS:……………. (Đề gồm có 03 trang) |
KIỂM TRA CUỐI HỌC KỲ II NĂM 2023 – 2024 |
Phần 1. Trắc nghiệm khách quan. (3,0 điểm)
Hãy khoanh tròn vào phương án đúng trong mỗi câu dưới đây:
Câu 1. [NB-1]Trong các cách viết sau đây, cách viết nào là phân số “âm hai phần năm”?
A.
B.
C.
D.
Câu 2. [NB-2] Cách viết nào sau đây biểu thị hỗn số?
A.
B.
C.
D.
Câu 3. [NB-3] Số đối của số thập phân -12,34 là:
A.
C.
C. 12,34
D. 0
Câu 4. [TH-TN4] Sắp xếp các số thập phân sau -5,9; 0,8;-7,3; 1,2; 3,41 theo thứ tự tăng dần, ta được:
A. -5,9 ;-7,3 ; 0,8 ; 1,2 ; 3,41.
B. 3,41 ; 1,2 ; 0,8 ;-5,9 ;-7,3.
C. -7,3 ;-5,9 ; 1,2 ; 3,41 ; 0,8.
D. -7,3 ;-5,9 ; 0,8 ; 1,2 ; 3,41.
Câu 5. [NB-4] Biển báo giao thông nào sau đây, không có trục đối xứng?

Câu 6. [NB-5] Chữ cái nào sau đây, có tâm đối xứng?
A. C
B. A
C. 0
D. U
Câu 7. [NB-6] Qua hai điểm A và B cho trước có bao nhiêu đường thẳng?
A. 2
B. 1
C. Nhiều hơn 2
D. Không có đường thẳng nào.
Câu 8. [NB-7] Điểm M là trung điểm của đoạn thẳng AB khi:
A. M nằm giữa A, B và MA = MB.
B. MA = MB.
C. M nằm giữa A và B.
D. MA = AB
Câu 9. [NB-TN9] Đoạn thẳng MN dài 10cm. Gọi I là trung điểm của đoạn thẳng MN. Khi đó, đoạn thẳng MI dài:
A. 5cm.
B. 5dm.
C. 2,5cm.
D. 2,5dm.
Câu 10. [NB-8] Góc có số đo bằng 900 là góc:
A. bẹt.
B. vuông.
C. nhọn.
D. tù.
Câu 11. [NB-9] Khả năng mặt sấp xuất hiện khi tung đồng xu là bao nhiêu?
A. 1
B. 0 .
C.
D.
Câu 12. [TH-TN12] Khả năng lấy được quả bóng màu đỏ trong hộp kín đựng 3 quả bóng (1 bóng xanh, 1 bóng vàng, 1 bóng đỏ) là bao nhiêu?
A. 0
B. 1
C.
D.
Phần 2: Tự luận (7,0 điểm)
Câu 13. (1 điểm) So sánh các số sau:
a) [TH-TL1] và
b) [TH-TL2] 6,345 và 6,325
Câu 14. (0,5 điểm) [VD-TL3] Một mảnh vườn có diện tích là 1600m² được trồng hai loại cây là cây sầu riêng và cây chôm chôm. Phần diện tích trồng cây chôm chôm chiếm diện tích cả vườn. Hỏi diện tích trồng cây sầu riêng là bao nhiêu mét vuông?
Câu 15. (1,0 điểm)
a) [VD-TL4] Tìm x, biết: x+24,4=-75,6
b) [VD-TL5] Tính diện tích một mảnh vườn hình chữ nhật có chiều dài 24,25 m và chiều rộng là 16,32m?
Câu 16. (0,75 điểm) [VD-TL6] Một cái ti vi giá 12500000 đồng. Tìm giá mới của nó sau khi giảm giá 20%?
Câu 17. (1,0 điểm) [TH-TL7] Hãy viết kí hiệu góc và viết số đo góc trên hình vẽ sau:
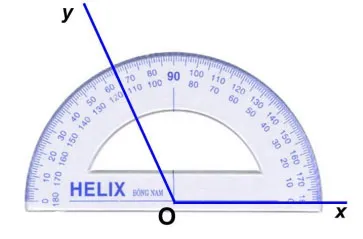
Câu 18. (1,5 điểm) Trong hình vẽ dưới đây:
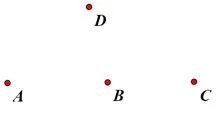
a) [NB-TL8] Hãy nêu ba điểm thẳng hàng và một bộ ba điểm không thẳng hàng?
b) [NB-TL9] Trong ba điểm A; B; C điểm nào nằm giữa?
Câu 19. (0,75 điểm) [TH-TL10] Trong hộp có 4 thẻ được đánh số 1,2,3,4. Thảo nhắm mắt lấy ra 1 thẻ từ hộp, ghi số rồi trả lại hộp. Lặp lại hoạt động trên 20 lần, Thảo được bảng kết quả như sau:

Hãy tính xác suất thực nghiệm của sự kiện: Thảo lấy được thẻ ghi số chẵn.
Câu 20. (0,5 điểm) [VDC-TL11] Một người đăng kí mua một căn hộ và trả tiền thành 3 đợt. Đợt đầu tiên, ngay khi kí hợp đồng mua bán, người đó phải trả số tiền mua căn hộ. Sáu tháng sau, người đó trả tiếp
số tiền mua căn hộ. Đọ̣t cuối, sau 1 năm kể từ khi kí hợp đồng, sẽ trả nốt số tiền còn lại là 800000000 đồng và nhận căn hộ. Hỏi số tiền để mua căn hộ là bao nhiêu?
1.2. Đáp án đề thi học kì 2 môn Toán 6
I. TRẮC NGHIỆM: (3,0 điểm) Mỗi phương án chọn đúng ghi 0,25điểm.
|
Câu |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
Đáp án |
A |
B |
C |
D |
D |
C |
B |
A |
A |
B |
C |
D |
II. TỰ LUẬN: (7,0 điểm)
|
Câu |
Lời giải |
Điểm |
|
13a |
|
0,5 |
|
b |
6,345 > 6,325 |
0,5 |
|
14 (0,5đ) |
Diện tích trồng cây chôm chôm là: Diện tích trồng cây sầu riêng là: 1600 – 400 = 1200 (m2) |
0,25 0,25 |
|
15a (0,5đ) |
x + 24,4 = -75,6 x = -75,6 – 24,4 = -100 |
0,5 |
|
b (0,5đ) |
Diện tích một mảnh vườn hình chữ nhật là: 24,25.16,32 = 395,76 (m2) |
0,5 |
|
16 (0,75đ) |
Ta có 100% – 20% = 80% Giá mới của ti vi sau khi giảm giá 20% là:
|
0,25 0,5 |
|
17 (1,0đ) |
Kí hiệu góc |
0,5 0,5 |
|
18a (1,0đ) |
* Ba điểm thẳng hàng là: A, B, C * Một bộ ba điểm không thẳng hàng là: A, B, D |
0,5 0,5 |
|
b (0,5đ) |
Trong ba điểm A; B; C điểm B nằm giữa |
0,5 |
|
19 (0,75đ) |
Số lần Thảo lấy được thẻ ghi số chẵn trong 20 lần thử là 10 Vậy xác suất thực nghiệm của sự kiện “Thảo lấy được thẻ ghi số chẵn” trong 20 lần thử là: |
0,25 0,5 |
|
20 (0,5đ)
|
Phân số biểu thị số tiền phải trả trong hai đợt đầu là: Phân số biểu thị số tiền phải trả trong đợt ba là: Do Vậy số tiền mua căn hộ là: |
0,25 0,25 |
1.3. Ma trận đề thi học kì 2 môn Toán 6
|
TT |
Chủ đề |
Nội dung/Đơn vị kiến thức |
Mức độ đánh giá |
Tổng % điểm |
|||||||
|
Nhận biết |
Thông hiểu |
Vận dụng |
Vận dụng cao |
||||||||
|
TNKQ |
TL |
TNKQ |
TL |
TNKQ |
TL |
TNKQ |
TL |
||||
|
1 |
Phân số (17 tiết) |
Phân số. Tính chất cơ bản của phân số. So sánh phân số |
2 (TN1,2) 0,5đ |
2,5 |
|||||||
|
Các phép tính với phân số |
1(TL1) 0,5đ |
1(TL3) 0,5đ |
1 (TL11) 1,0đ |
||||||||
|
2 |
Số thập phân (11 tiết) |
Số thập phân và các phép tính với số thập phân. Tỉ số và tỉ số phần trăm |
1 (TN3) |
1 (TN4) |
1(TL2) 0,5đ |
3 (TL4,5,6) 1,5đ |
2,5 |
||||
|
3 |
Tính đối xứng của hình phẳng trong thế giới tự nhiên (9 tiết) |
Hình có trục đối xứng |
1 (TN5) |
0,5 |
|||||||
|
Hình có tâm đối xứng |
1 (TN6) |
||||||||||
|
Vai trò của tính đối xứng trong thế giới tự nhiên |
|||||||||||
|
4 |
Các hình hình học cơ bản (20 tiết) |
Điểm, đường thẳng, tia |
1 (TN7) |
2 (TL8, 9) 1,5đ |
3,5 |
||||||
|
Đoạn thẳng. Độ dài đoạn thẳng |
2 (TN8,9) |
||||||||||
|
Góc. Các góc đặc biệt. Số đo góc |
1 (TN10) |
1 (TL7) 1,0đ) |
|||||||||
|
5 |
Một số yếu tố xác suất. (7 tiết) |
Làm quen với một số mô hình xác suất đơn giản. Làm quen với việc mô tả xác suất (thực nghiệm) của khả năng xảy ra nhiều lần của một sự kiện trong một số mô hình xác suất đơn giản. |
1 (TN11) |
1,0 |
|||||||
|
Mô tả xác suất (thực nghiệm) của khả năng xảy ra nhiều lần của một sự kiện trong một số mô hình xác suất đơn giản |
1 (TN12) |
1 (TL10) 0,5 |
|||||||||
|
Tổng: Số câu Điểm |
10 2,5 |
3 2,5 |
2 0,5 |
3 1,5 |
4 2,0 |
1 1,0 |
23 10,0 |
||||
|
Tỉ lệ % |
50% |
20% |
20% |
10% |
100% |
||||||
|
Tỉ lệ chung |
70% |
30% |
100% |
||||||||
1.4. Bản đặc tả đề thi học kì 2 môn Toán 6
| TT | Chương/Chủ đề | Mức độ đánh giá | Số câu hỏi theo mức độ nhận thức | ||||
| Nhận biết | Thông hiểu | Vận dụng | Vận dụng cao | ||||
| SỐ – ĐẠI SỐ | |||||||
|
1
|
Phân số |
Phân số. Tính chất cơ bản của phân số. So sánh phân số
|
Nhận biết: – Nhận biết được phân số với tử số hoặc mẫu số là số nguyên âm. |
1TN (TN1) |
|||
|
– Nhận biết được khái niệm hai phân số bằng nhau và nhận biết được quy tắc bằng nhau của hai phân số. |
|||||||
|
– Nêu được hai tính chất cơ bản của phân số. |
|||||||
|
– Nhận biết được số đối của một phân số. |
|||||||
|
– Nhận biết được hỗn số dương. |
1TN (TN2) |
||||||
|
Thông hiểu: – So sánh được hai phân số cho trước. |
1TL (TL1) |
||||||
|
Các phép tính với phân số |
Vận dụng: – Thực hiện được các phép tính cộng, trừ, nhân, chia với phân số. – Vận dụng được các tính chất giao hoán, kết hợp, phân phối của phép nhân đối với phép cộng, quy tắc dấu ngoặc với phân số trong tính toán (tính viết và tính nhẩm, tính nhanh một cách hợp lí). – Tính được giá trị phân số của một số cho trước và tính được một số biết giá trị phân số của số đó. Giải quyết được một số vấn đề thực tiễn (đơn giản, quen thuộc) gắn với các phép tính về phân số (ví dụ: các bài toán liên quan đến chuyển động trong Vật lí,…). |
1TL (TL11) |
|||||
|
Vận dụng cao: – Giải quyết được một số vấn đề thực tiễn (phức hợp, không quen thuộc) gắn với các phép tính về phân số. |
|||||||
|
2 2 2 |
Số thập phân |
Số thập phân và các phép tính với số thập phân. Tỉ số và tỉ số phần trăm |
Nhận biết: – Nhận biết được số thập phân âm, số đối của một số thập phân. |
1TN (TN3) |
|||
|
Thông hiểu: – So sánh được hai số thập phân cho trước. |
1TN (TN4) |
1TL (TL2) |
|||||
|
Vận dụng: – Thực hiện được các phép tính cộng, trừ, nhân, chia với số thập phân. – Vận dụng được các tính chất giao hoán, kết hợp, phân phối của phép nhân đối với phép cộng, quy tắc dấu ngoặc với số thập phân trong tính toán (tính viết và tính nhẩm, tính nhanh một cách hợp lí). – Thực hiện được ước lượng và làm tròn số thập phân. – Tính được tỉ số và tỉ số phần trăm của hai đại lượng. – Tính được giá trị phần trăm của một số cho trước, tính được một số biết giá trị phần trăm của số đó. Giải quyết được một số vấn đề thực tiễn (đơn giản, quen thuộc) gắn với các phép tính về số thập phân, tỉ số và tỉ số phần trăm (ví dụ: các bài toán liên quan đến lãi suất tín dụng, liên quan đến thành phần các chất trong Hoá học,…). |
3TL (TL4,5,6) |
||||||
|
Vận dụng cao: – Giải quyết được một số vấn đề thực tiễn (phức hợp, không quen thuộc) gắn với các phép tính về số thập phân, tỉ số và tỉ số phần trăm. |
|||||||
|
HÌNH HỌC VÀ ĐO LƯỜNG |
|||||||
|
3 |
Tính đối xứng của hình phẳng trong thế giới tự nhiên |
Hình có trục đối xứng |
Nhận biết: – Nhận biết được trục đối xứng của một hình phẳng. |
||||
|
– Nhận biết được những hình phẳng trong tự nhiên có trục đối xứng (khi quan sát trên hình ảnh 2 chiều). |
1TN (TN5) |
||||||
|
Hình có tâm đối xứng |
Nhận biết: – Nhận biết được tâm đối xứng của một hình phẳng. |
||||||
|
– Nhận biết được những hình phẳng trong thế giới tự nhiên có tâm đối xứng (khi quan sát trên hình ảnh 2 chiều). |
1TN (TN6) |
||||||
|
Vai trò của tính đối xứng trong thế giới tự nhiên |
Nhận biết: – Nhận biết được tính đối xứng trong Toán học, tự nhiên, nghệ thuật, kiến trúc, công nghệ chế tạo,… |
||||||
|
– Nhận biết được vẻ đẹp của thế giới tự nhiên biểu hiện qua tính đối xứng (ví dụ: nhận biết vẻ đẹp của một số loài thực vật, động vật trong tự nhiên có tâm đối xứng hoặc có trục đối xứng). |
|||||||
|
4 4 |
Các hình hình học cơ bản |
Điểm, đường thẳng, tia |
Nhận biết: – Nhận biết được những quan hệ cơ bản giữa điểm, đường thẳng: điểm thuộc đường thẳng, điểm không thuộc đường thẳng; tiên đề về đường thẳng đi qua hai điểm phân biệt. |
1TN (TN7) |
|||
|
– Nhận biết được khái niệm hai đường thẳng cắt nhau, song song. |
|||||||
|
– Nhận biết được khái niệm ba điểm thẳng hàng, ba điểm không thẳng hàng. |
1TL (TL10) |
||||||
|
– Nhận biết được khái niệm điểm nằm giữa hai điểm. |
1TL (TL11) |
||||||
|
– Nhận biết được khái niệm tia. |
|||||||
|
Đoạn thẳng. Độ dài đoạn thẳng |
Nhận biết: – Nhận biết được khái niệm đoạn thẳng, trung điểm của đoạn thẳng, độ dài đoạn thẳng. |
2TN (TN8,9) |
|||||
|
Góc. Các góc đặc biệt. Số đo góc |
Nhận biết: – Nhận biết được khái niệm góc, điểm trong của góc (không đề cập đến góc lõm). |
||||||
|
– Nhận biết được các góc đặc biệt (góc vuông, góc nhọn, góc tù, góc bẹt). |
1TN (TN10) |
||||||
|
– Nhận biết được khái niệm số đo góc. |
1TL (TL7) |
||||||
|
MỘT SỐ YẾU TỐ THỐNG KÊ VÀ XÁC SUẤT |
|||||||
|
5 |
Một số yếu tố xác suất. |
Làm quen với một số mô hình xác suất đơn giản. Làm quen với việc mô tả xác suất (thực nghiệm) của khả năng xảy ra nhiều lần của một sự kiện trong một số mô hình xác suất đơn giản. |
Nhận biết: – Làm quen với mô hình xác suất trong một số trò chơi, thí nghiệm đơn giản (ví dụ: ở trò chơi tung đồng xu thì mô hình xác suất gồm hai khả năng ứng với mặt xuất hiện của đồng xu, …). |
1TN (TN11) |
|||
|
Thông hiểu: – Làm quen với việc mô tả xác suất (thực nghiệm) của khả năng xảy ra nhiều lần của một sự kiện trong một số mô hình xác suất đơn giản. |
1TN (TN12) 1TL (TL10) |
||||||
|
Mô tả xác suất (thực nghiệm) của khả năng xảy ra nhiều lần của một sự kiện trong một số mô hình xác suất đơn giản |
Vận dụng: – Sử dụng được phân số để mô tả xác suất (thực nghiệm) của khả năng xảy ra nhiều lần thông qua kiểm đếm số lần lặp lại của khả năng đó trong một số mô hình xác suất đơn giản. |
||||||
2. Đề thi học kì 2 môn Toán 6 sách Chân trời sáng tạo – Đề 2
2.1. Ma trận đề thi học kì 2 môn Toán 6
| Mức độ Chủ đề | Nhận biết | Thông hiểu | Vận dụng thấp | Vận dụng cao | Tổng | ||||
| TNKQ | TL | TNKQ | TL | TNKQ | TL | TNKQ | TL | ||
|
1. Phân số |
– Biết được quy tắc cộng, trừ phân số. – Biết được các tính chất của phép cộng phân số. – Biết được số đối của một phân số. – Biết được quy tắc nhân và chia phân số. – Biết được các tính chất của phép nhân. – Biết được phân số nghịch đảo. – Biết được quy tắc tìm giá trị phân số của một số cho trước và quy tắc tìm một số biết giá trị phân số của số đó. – – Biết viết hỗn số thành phân số |
Thực hiện được phép nhân và chia phân số. -Thực hiện rút gọn được phân số. |
– Thực hiện biến đổi và so sánh được các phân số |
|
|||||
|
Số câu Số điểm Tỉ lệ |
4 0,8 8% |
|
2 0,4 4% |
1 1,5 15% |
1 0,2 2% |
|
8 2,9đ 29% |
||
|
2. Số thập phân |
– Biết được cách quy các phép toán với số thập phân bất kì về các phép toán với số thập phân dương. – Biết được các tính chất giao hoán, kết hợp, phân phối của phép nhân đối với phép cộng, quy tắc dấu ngoặc với số thập phân trong tính toán. – Biết được thế nào là làm tròn số; làm tròn số thập phân đến một hàng nào đó. – Biết được thế nào là ước lượng kết quả của một phép đo, phép tính; ước lượng dùng làm gì. |
– Thực hiện được các phép tính cộng, trừ, nhân, chia số thập phân. Sử dụng được kí hiệu tỉ số, tỉ số phần trăm của hai số. |
|
||||||
|
Số câu Số điểm Tỉ lệ |
2 0,4 4% |
|
1 0,2 2% |
1 0,5đ 5% |
|
|
|
4 1,1đ 11% |
|
|
3. Dữ liệu và xác suất thực nghiệm |
– Biết được các loại dữ liệu, chủ yếu là phân biệt được dữ liệu là số (dữ liệu định lượng) và dữ liệu không phải là số (dữ liệu định tính). – Biết được một số cách đơn giản để thu thập dữ liệu như lập phiếu hỏi, làm thí nghiệm, quan sát hay thu thập từ những nguồn có sẵn như sách báo, trang web,… – Đọc và phân tích được dữ liệu từ bảng thống kê và biểu đồ tranh – Nhận ra được vấn đề hoặc quy luật đơn giản từ việc phân tích biểu đồ cột. – Nhận ra được quy luật đơn giản từ biểu đồ cột kép. |
– Biết được tính không đoán trước được trong kết quả của một số trò chơi, thí nghiệm. – Biết được một sự kiện trong trò chơi, thí nghiệm có thể xảy ra hay không. – Biểu diễn được khả năng xảy ra một sự kiện theo xác suất thực nghiệm
|
– Vẽ được biểu đồ cột từ bảng số liệu cho trước. – Đọc và mô tả được dữ liệu từ biểu đồ cột. – Vẽ được biểu đồ cột kép. – Đọc và mô tả được dữ liệu từ biểu đồ cột kép. |
– Liệt kê được các kết quả có thể xảy ra trong các trường hợp cụ thể. – Kiểm tra được một sự kiện xảy ra hay không xảy ra. – Sử dụng được phân số để mô tả xác suất (thực nghiệm) của khả năng xảy ra nhiều lần thông qua kiểm đếm số lần lặp lại của khả năng đó trong một số mô hình xác suất đơn giản. |
|
||||
|
Số câu Số điểm Tỉ lệ |
2 0,4 4% |
|
2 0,4 4% |
|
|
1 1đ 10% |
|
1 1đ 10% |
6 2,8đ 28% |
|
4. Những hình học cơ bản |
– Nhận biết được một tia. Biết được khái niệm trung điểm của đoạn thẳng. – Biết đo độ dài đoạn thẳng để xác định trung điểm của đoạn thẳng. Biết được khái niệm góc; đỉnh và cạnh của góc; góc bẹt; điểm trong của góc. Biết được khái niệm số đo góc, các góc đặc biệt (góc vuông, góc nhọn, góc tù) |
Thực hiện đo một góc bằng thước đo góc. Tìm được mối liên hệ số đo giữa các góc đặc biệt. |
Giải được các bài toán liên quan đến trung điểm của đoạn thẳng |
|
|||||
|
4 0,8 8% |
1 1 10% |
2 0,4 4% |
|
1 1 10% |
8 3,2đ 32% |
||||
|
T. Số câu T. Số điểm Tỉ lệ |
13 3,4 34% |
9 3,4 34% |
3 2,2 22% |
1 1 10% |
26 10 100% |
||||
2.2. Đề thi học kì 2 môn Toán 6
|
PHÒNG GD&ĐT……. |
ĐỀ KIỂM TRA HỌC KỲ II, NĂM HỌC 2023-2024 |
A. TRẮC NGHIỆM (4 điểm): Viết chữ cái đứng trước câu trả lời em cho là đúng vào giấy kiểm tra:
Câu 1: Kết quả của phép tính là:
A. 0
B.
C.
D.
Câu 2: Kết quả của phép tính là:
A.
B.
C.
D.
Câu 3: của 56 bằng:
A. 14.
B. 224.
C.60.
D. 52.
Câu 4: Phân số nghịch đảo của phân số là:
A.
B.
C.
D.
Câu 5: Kết quả của phép tính 4,52 + 11,3 là :
A. 56,5.
B. 5,56.
C. 15,82.
D. 1,582.
Câu 6: Kết quả của phép tính 1+ 12,3 – 11,3 là:
A. 11.
B. -11.
C. 2.
D. -2.
Câu 7: So sánh và
, ta được:
A.  frac{25+3}{8}” width=”107″ height=”41″ data-type=”0″ data-latex=”3frac{3}{4} > frac{25+3}{8}” data-src=”https://tex.vdoc.vn?tex=3%5Cfrac%7B3%7D%7B4%7D%20%3E%20%5Cfrac%7B25%2B3%7D%7B8%7D”>
frac{25+3}{8}” width=”107″ height=”41″ data-type=”0″ data-latex=”3frac{3}{4} > frac{25+3}{8}” data-src=”https://tex.vdoc.vn?tex=3%5Cfrac%7B3%7D%7B4%7D%20%3E%20%5Cfrac%7B25%2B3%7D%7B8%7D”>
B.
C.
D.  3frac{3}{4}” width=”107″ height=”41″ data-type=”0″ data-latex=”frac{25+3}{8} > 3frac{3}{4}” data-src=”https://tex.vdoc.vn?tex=%5Cfrac%7B25%2B3%7D%7B8%7D%20%3E%203%5Cfrac%7B3%7D%7B4%7D”>
3frac{3}{4}” width=”107″ height=”41″ data-type=”0″ data-latex=”frac{25+3}{8} > 3frac{3}{4}” data-src=”https://tex.vdoc.vn?tex=%5Cfrac%7B25%2B3%7D%7B8%7D%20%3E%203%5Cfrac%7B3%7D%7B4%7D”>
Câu 8: Làm tròn số 231, 6478 đến chữ số thập phân thứ hai:
A. 231, 64.
B. 231, 65.
C. 23.
D. 231, 649.
Câu 9: Hỗn số được viết dưới dạng phân số?
A.
B.
C.
D.
Câu 10: Phân số được rút gọn đến tối giản là:
A.
B.
C.
D.
Câu 11: Cho biểu đồ tranh ở Hình 3:

Số học sinh (HS) yêu thích Cam là:
A. 50 HS.
B. 55 HS.
C. 40 HS.
D. 45 HS.
Câu 12: Biểu đồ cột kép thể hiện số học sinh nam, nữ ở mỗi lớp của khối 6 ở một trường THCS như sau:
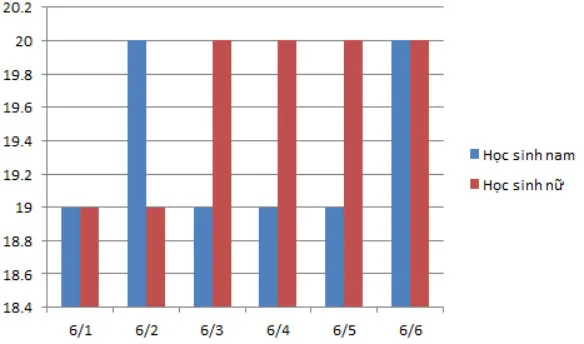
Số học sinh nam/nữ của lớp 6/4 là:
A. 19/19.
B. 20/19.
C. 19/20.
D. 20/20.
Câu 13: Khi gieo hai con xúc sắc, gọi T là tổng số chấm trên hai con xúc sắc thì kết quả nào sau đây không thể xảy ra?
A. T = 4.
B. T = 3.
C. T = 2.
D. T = 1.
Câu 14: Cô giáo tổ chức trò chơi chiếc nón kì diệu, bạn A tham gia quay chiếc nón 5 lần thì được 2 lần vào ô may mắn. Hỏi xác suất thực nghiệm của sự kiện quay vào ô may mắn là:
A.
B.
C.
D.
Câu 15: Cho hình vẽ: Có bao nhiêu tia gốc A trong hình vẽ đã cho:
A. 1
B. 2
C.3
D. 4

Câu 16: Cho góc Hỏi số đo của
bằng mấy phần số đo của góc bẹt?
A.
B.
C.
D.
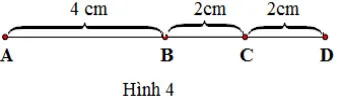
Câu 17: Xem hình 4:
A. Điểm C là trung điểm của đoạn thẳng AB.
B. Điểm C là trung điểm của đoạn thẳng BD.
C. Điểm C là trung điểm của đoạn thẳng AD.
D. Điểm B là trung điểm của đoạn thẳng AC.
Câu 18: Hình gồm hai tia chung gốc Ox, Oy được gọi là:
A. Góc xOy.
B. Góc Oxy.
C. Góc xyO.
D. Góc bẹt.
Câu 19: Góc nhọn là góc :
A. Nhỏ hơn góc bẹt.
B. Nhỏ hơn góc vuông.
C. Có số đo bằng .
D. Có số đo .
Câu 20: Xem hình 5:
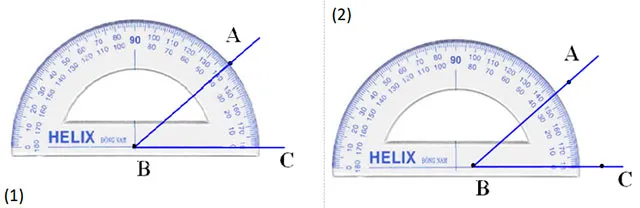
Hình đặt thước đo góc đúng và số đo của là:
A. (1),
B. (1),
C. (2),
D. (2),
B. TỰ LUẬN (6 điểm):
Câu 1 (1,5 điểm): Tính giá trị của biểu thức:
a) 152,3 + 2021,19 + 7,7 – 2021,19
b)
Câu 2 (0,5 điểm): Tìm tỉ số phần trăm của hai số 12 và 15.
Câu 3 (1 điểm): Hãy vẽ biểu đồ cột thể hiện số học sinh ở mỗi lớp của khối 6 ở một trường THCS theo bảng sau:
|
Lớp |
6/1 |
6/2 |
6/3 |
6/4 |
|
Số học sinh |
38 |
39 |
40 |
39 |
Câu 4 (1 điểm): Gieo 02 con xúc xắc, liệt kê các kết quả có thể để sự kiện tổng số chấm ở hai con xúc xắc là một số nguyên tố.
Câu 5 (2 điểm): Vẽ tia Ot. Trên tia Ot, lấy hai điểm M, N sao cho OM = 4cm, ON = 8 cm.
a) Trong ba điểm O, M, N điểm nào nằm giữa hai điểm còn lại? Vì sao?
b) Tính MN. Điểm M có là trung điểm của đoạn thẳng ON không? Vì sao?
2.3. Đáp án đề thi học kì 2 môn Toán 6
A. TRẮC NGHIỆM (Đúng mỗi câu 0.2 điểm):
|
Câu |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
|
Đáp án |
C |
B |
A |
D |
D |
C |
A |
B |
B |
B |
D |
C |
D |
A |
C |
D |
B |
A |
B |
A |
B. TỰ LUẬN
|
Câu 1 : Tính giá trị của biểu thức: a) 12,3 + 2021,19 + 7,7 – 2021,19 = (12,3 + 7,7) + (2021,19 – 2021,19) = 20 + 0 = 20 b) |
0.5 điểm 0.25 điểm 0.25 điểm 0.5 điểm |
|
Câu 2 : Tỉ số của hai số 12 và 15 là |
0,5 điểm |
|
Câu 3: Biểu đồ cột thể hiện số học sinh ở mỗi lớp của khối 6 ở một trường THCS
|
1 điểm |
|
Câu 4: Gieo 02 con xúc xắc, liệt kê các kết quả có thể để sự kiện tổng số chấm ở hai con xúc xắc là một số nguyên tố. Gọi x là số chấm của 1 xúc xắc, y là số chấm của xúc xắc còn lại Ta có (x ; y) sao cho x+y là số nguyên tố ( 1;1), (1 ; 2), (1 ;4), (1 ;6), ( 2;3), ( 2;5), ( 3;1), ( 3;4), ( 4;1),( 5;1), ( 5;6), ( 6;1). |
0.25 điểm 0.25 điểm 0.5 điểm |
|
Câu 5: Hình vẽ đúng a) Vì OM b) Ta có : OM + MN = ON MN = ON – OM = 8 – 4 MN = 4cm. Vậy : M là trung điểm của đoạn thẳng ON vì M nằm giữa O, N và OM = MN = 3cm. |
1 điểm 0.5 điểm 0.5 điểm |
…..
>> Tải file để tham khảo trọn bộ đề thi!