Download.vn Học tập Thi THPT Quốc Gia Toán Ngoại ngữ
Bạn đang đọc: Bộ đề thi thử THPT Quốc gia 2019 trường THPT Kinh Môn II, Hải Dương
Bộ đề thi thử THPT Quốc gia 2019 trường THPT Kinh Môn II, Hải Dương Đề thi minh họa môn Toán THPT Quốc gia 2019
Giới thiệu Tải về Bình luận
- 1
Mua tài khoản Download Pro để trải nghiệm website Download.vn KHÔNG quảng cáo & tải File cực nhanh chỉ từ 79.000đ. Tìm hiểu thêm Mua ngay
Với mong muốn cung cấp thêm nhiều tài liệu ôn tập hữu ích dành cho các bạn học sinh lớp 12. Download.vn xin gửi đến các bạn Bộ đề thi thử THPT Quốc gia 2018 trường THPT Kinh Môn II, Hải Dương.
Đề thi có đáp án kèm theo sẽ giúp các bạn ôn luyện và làm quen với cấu trúc đề thi môn Toán để rút kinh nghiệm cho kỳ thi THPT Quốc gia năm 2019 sắp tới. Chúc các bạn ôn tập và đạt được kết quả cao. Ngoài ra các bạn có thể tham khảo thêm rất nhiều tài liệu đề thi thử THPT Quốc gia tại Download.vn để có thể tải về những tài liệu hay nhất nhé.
Đề thi minh họa môn Toán THPT Quốc gia 2019
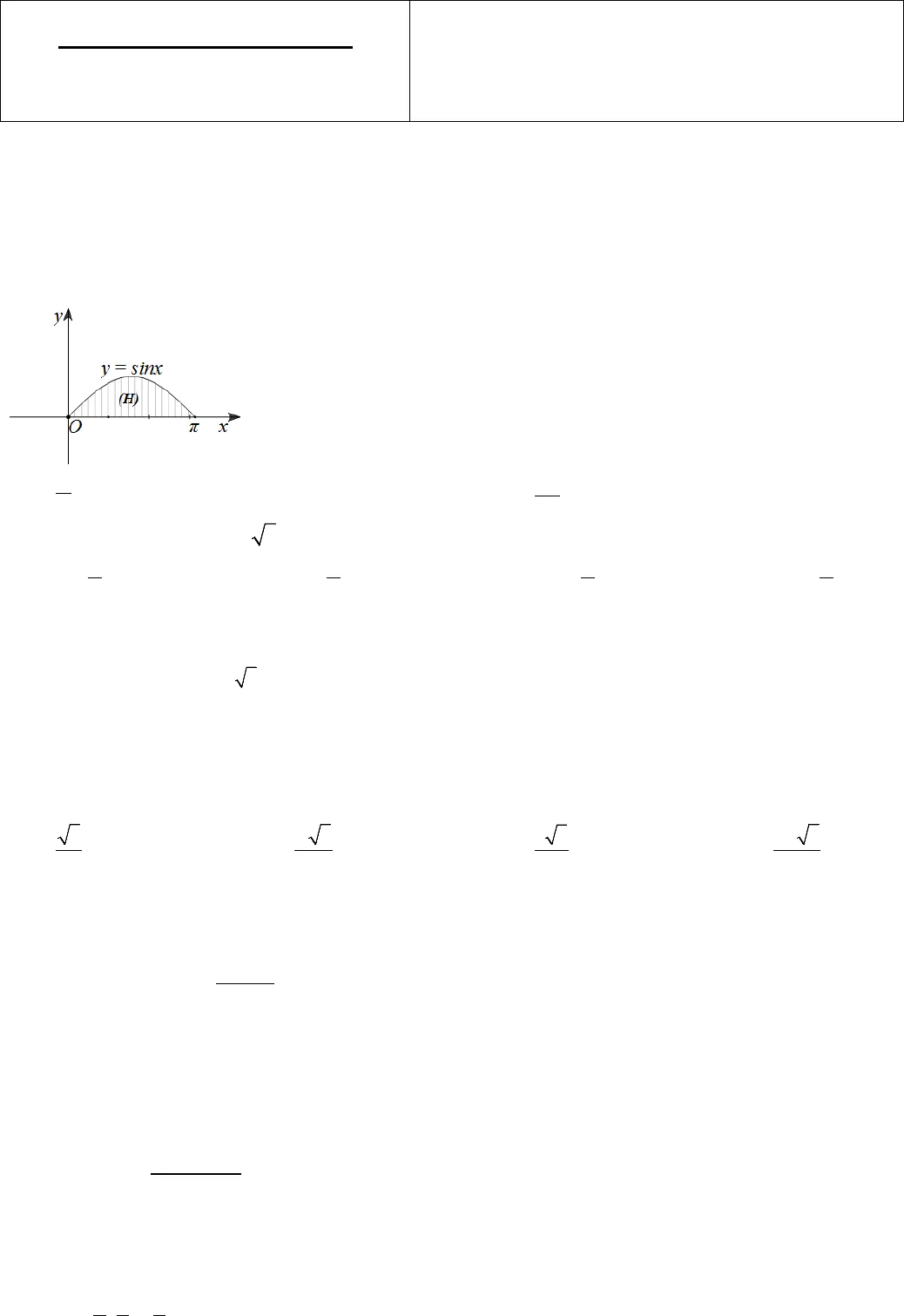Trang 1/5 – Mã đề thi 132 TRƯỜNG THPT KINH MÔN II Mã đề thi: 132ĐỀ THI THỬ THPT QUỐC GIA – Lần 3Môn: ToánThời gian làm bài: 90 phút; (50 câu trắc nghiệm)(Thí sinh không được sử dụng tài liệu) Họ, tên thí sinh:……………………..……………………………………. Mã số: ………………………..Câu 1: Cho hình ( )Htrong hình vẽ dưới đây quay quanh trụcOxtạo thành một khối tròn xoay có thể tích bằng bao nhiêu ? A..2πB.22.πC.2.2πD.2.πCâu 2: Phương trình cot 3 0x +=có nghiệm làA.π2π3xk= +B.ππ6xk= +C.π2π6xk=−+ D. ππ6xk=−+Câu 3: Cho hình trụ ()Tcó hai hình tròn đáy là ()Ovà ( ‘).OXét hình nón ()Ncó đỉnh ‘,Ođáy là hình tròn ( )Ovà đường sinh hợp với đáy một góc.αBiết tỉ số giữa diện tích xung quanh hình trụ ()Tvà diện tích xungquanh hình nón()Nbằng 3.Tính số đo góc .αA.075 .=αB.045 .=αC.060 .=αD.030 .=αCâu 4: Ông An, gửi ngân hàng 150 triệu đồng với lãi suất 0,8%/tháng, sau mỗi tháng tiền lãi được nhập vào vốn(lãi kép). Hỏi sau một năm số tiền lãi ông An thu được gần nhất với kết quả nào sau đây. A. 15.050.000 đồng.B. 165.050.000 đồng.C. 165.051.000 đồng.D. 15.051.000 đồng.Câu 5: Một khối cầu ngoại tiếp khối lập phương. Tỉ số thể tích giữa khối cầu và khối lập phương là A.3.2B.3.2πC.33.8 D.33.8πCâu 6: Trong không gian Oxyz, cho ( ) ( ) ( ) ( ) ( )1; 2; 2 , 2;1; 2 , 1; 5;1 , 3;1;1 , 0; 1; 2A B C DE−−. Có bao nhiêu mặtphẳng cách đều 5 điểm đã cho A. Vô sốB. 1C. 2D. 3Câu 7: Cho hàm số 12mxyxm+=−với tham số0m ≠.Giao điểm của hai đường tiệm cận của đồ thị hàm số thuộcđường thẳng có phương trình nào dưới đây ? A.2yx=.B.20xy+=.C.20xy−=.D.20xy+=.Câu 8: Trong không gian với hệ tọa độ Oxyzcho hai điểm (1;1; 2)Avà (3; 3; 6)BPhương trình mặt phẳng trungtrực của đoạn AB là A.2 12 0.xy z−− + =B.2 12 0.xy z++ − =C.2 8 0.xy z−+ −=D.2 4 0.xy z+− +=Câu 9: Giả sử 2201d ln 5 ln 3; ,43xx a b abxx−=+∈++∫. Tính22Pa b= −. A.10P =.B.8P =.C.3P =.D.1P =.Câu 10: Trong không gian Oxyz, cho điểm (1;4;2)Mvà mặt phẳng( ):x y z 1 0α++−=. Xác định tọa độ điểmH là hình chiếu vuông góc của điểmMtrên mặt phẳng ()αA.45 1H( ; ; ).33 3−−B. H(1;4;-4) C.H( 1; 2; 0).−D.H(3;6;4).
Trang 2/5 – Mã đề thi 132 Câu 11: Cho hàm số 1(C)1xyx. Điểm M thuộc (C) có hoành độ lớn hơn 1, tiếp tuyến của (C) tại M cắthai tiệm cận của (C) lần lượt tại A, B. Diện tích nhỏ nhất của tam giác OAB bằng. A.4 22B.4C.42D.42Câu 12: Tính diện tích hình phẳng giới hạn bởi đồ thị của hai hàm số 2y x4=−+và y x2=−+A.5.7B.8.3C.9.2D. 9. Câu 13: Số giá trị nguyên của tham số mđể hàm số 22mxyxm−=−+nghịch biến trên khoảng1;2+∞là A.4. B.3. C.5. D.2. Câu 14: Một mảnh đất hình chữ nhật ABCDcó chiều dài25AB m=, chiều rộng20AD m=được chia thànhhai phần bằng nhau bởi vạch chắnMN(, MNlần lượt là trung điểmBCvàAD). Một đội xây dựng làm mộtcon đường đi từAđếnCqua vạch chắn MN, biết khi làm đường trên miền ABMNmỗi giờ làm được 15mvàkhi làm trong miềnCDNMmỗi giờ làm được30m. Tính thời gian ngắn nhất mà đội xây dựng làm được conđường đi từAđến Clà.A.253 B. 10 2 72530+ C. 20 72530+D.5Câu 15: Cho hình hình chóp S.ABC có cạnh SA vuông góc với mặt đáy và SA=3a. Đáy ABC là tam giácđều cạnh bằnga. Thể tích của khối chóp S.ABC bằngA.33.12aV=B.3.4aV=C.33Va=D.3.12aV=Câu 16: Trong không gian ,Oxyzmặt phẳng ()Oyzcó phương trình làA.0.yz+=B.0.z =C.0.y =D.0.x =Câu 17: Họ nguyên hàm của hàm số cos 2fx xlàA.cos 2 d sin 2xx x C. B. cos 2 d 2 sin 2xx x C. C.sin 2cos 2 d2xxx C. D. sin 2cos 2 d2xxx C . Câu 18: Cho hình chóp S.ABCD đều, có cạnh bên bằng 1. Thể tích lớn nhất của khối chóp S.ABCD bằng A.427B.16C.4327 D. 312Câu 19: Đạo hàm của hàm số .4xyx=là: A.( )’ 4 1 ln 4 .xyx= +B.()’ 4 1 ln 4 .xy = +C.2′ ln 4.yx= D. ‘ 4 ln 4.xyx=Câu 20: Đường cong ở hình vẽ dưới đây là đồ thị của hàm số nào dưới đây ? A.12.xy−=B.12.yx−=C.1.yx−=D.( )2log 2 .yx=Câu 21: Trong không gian với hệ trục tọa độ Oxyz, cho hai véctơ ( )1; 2;1u = −và ( )2;1; 1 .v = −Véctơ nào dưới đây vuông góc với cả hai véctơuvà v?A.( )21;3;5 .w = − B. ( )41; 4; 7 .w = C. ( )31; 4; 7 .w = − D. ( )12; 6; 10 .w =−−− Câu 22: Tập nghiệm của bất phương trình 4 3.2 2 0xx− +>làA.( ) ( );1 2; .x ∈ −∞ ∪ +∞B.( )0;1 .x ∈C.( ) ( ); 0 1; .x ∈ −∞ ∪ +∞D.( )1; 2 .x ∈
Trang 3/5 – Mã đề thi 132 Câu 23: Hệ số của 5xtrong khai triển biểu thức ( ) ( )6821 31xx x−+ −bằngA.13848−B.13368C.13848D.13368−Câu 24: Trong không gian Oxyz, cho hai điểm(1; 2;3),I −(0;1;5).MPhương trình mặt cầu có tâm Ivà đi qua MlàA.2 22( 1) ( 2) ( 3) 14.xy z− ++ +− = B. 2 22( 1) ( 2) ( 3) 14.xy z+ +− ++ =C.2 22( 1) ( 2) ( 3) 14.xy z+ +− ++ = D. 2 22( 1) ( 2) ( 3) 14.xy z− ++ +− =Câu 25: Cho số phức 2(1 2 )zi= +. Xác định phần thực a, phần ảobcủa số phức 1zA.34;.25 25ab=−=−B.3; 4.ab=−=−C.34;.25 25ab=−=D.3; 4.ab=−=Câu 26: Cho số phức 23zi= +. Phần thực và phần ảo của số phứczlần lượt là: A. Phần thực bằng 2, phần ảo bằng3−B. Phần thực bằng 3, phần ảo bằng2C. Phần thực bằng 2−, phần ảo bằng3−D. Phần thực bằng 3, phần ảo bằng2−. Câu 27: Thể tích khối nón có chiều cao bằng 2,bán kính hình tròn đáy bằng 5 làA.25 .πB.50.3π C. 200.3πD.50 .πCâu 28: Trong không gian Oxyz, cho mặt phẳng (P):3 10xy− + +=. Tính góc tạo bởi (P) với trục OxA.060B.030C.0120D.0150Câu 29: Cho hàm số ( )fxliên tục trên .Mệnh đề nào sau đây đúng?A.( )( )12001.2f x dx f x dx=∫∫ B. ( ) ( )11102.f x dx f x dx−=∫∫ C. ( )110.f x dx−=∫D.( ) ( )11001.f x dx f x dx= −∫∫Câu 30: Trong không gian tọa độ Oxyz, cho đường thẳng x1 y2 z9d:13 1−−−= =−và mặt phẳng()αcó phươngtrình2m x my 2z 19 0− −+=với m là tham số. Tập hợp các giá trị m thỏa mãnd / /( )αlà A.{ }2B.{ }1; 2C.{}1D.∅Câu 31: Để hàm số −+≠=−=22x 3x 1khix 1f(x)2(x 1)m khix 1liên tục tại x = 1 thì giá trị của m bằng:A. 0,5 B. 1,5 C. 1 D. 2 Câu 32: Tập xác định của hàm số 322532 3yx x x là A. ;1 2; 3D . B. ; 1; 2D . C. ; 3D . D. ;1 2;D . Câu 33: Gọi Tlà giá trị lớn nhất của hàm số 323 91yx x x trên đoạn2;1 .Tính giá trịTA.4T B.1T C.20.T D.6.T Câu 34: Cho số phức z thỏa mãn −+ =1 3 32zi. Biết rằng số phức()=− ++2019(1 ) 3 2019w i zicó tập hợp các điểm biểu diễn thuộc đường tròn (C). Diện tích S của hình tròn (C) bằng A.π18B.π36C.π9D.π12Câu 35: Trong không gian cho A(1;2;3), B(2;–1;2). Đường thẳng đi qua hai điểm AB có phương trình là A.1233xtytzt= += −=−−B.1231 31xy z−−−= =− C. 21213 1x yz− +−= =−−D.324612xtytzt= +=−−= −Câu 36: Tìm tất cả các giá trị của tham số mđể đồ thị hàm số( )42 241yx m x m= + − +−có một điểm cực trị.A.( 2; 2)m∈−. B.( ) ( ); 2 2;m∈ −∞ − ∪ +∞. 