Download.vn Học tập Lớp 12 Thi THPT Quốc Gia Văn

Bạn đang đọc: Bộ đề thi thử THPT Quốc gia 2020 trường THPT Chuyên Thái Bình

Bộ đề thi thử THPT Quốc gia 2020 trường THPT Chuyên Thái Bình Đề minh họa THPT Quốc gia năm 2020 môn Toán

Giới thiệu Tải về Bình luận

• 6

Mua tài khoản Download Pro để trải nghiệm website Download.vn KHÔNG quảng cáo & tải File cực nhanh chỉ từ 79.000đ. Tìm hiểu thêm Mua ngay

Ngày thi THPT Quốc gia 2020 đang ngày một đến gần, Download.vn xin giới thiệu đến các bạn tài liệu Đề thi thử THPT Quốc gia 2020 trường THPT Chuyên Thái Bình.

Hy vọng đây là tài liệu bổ ích giúp các bạn học sinh lớp 12 rèn luyện kỹ năng làm bài và làm quen với cấu trúc đề thi. Nội dung chi tiết mời các bạn cùng tham khảo và tải tài liệu tại đây.

Đề thi thử THPT Quốc gia 2020 môn Toán

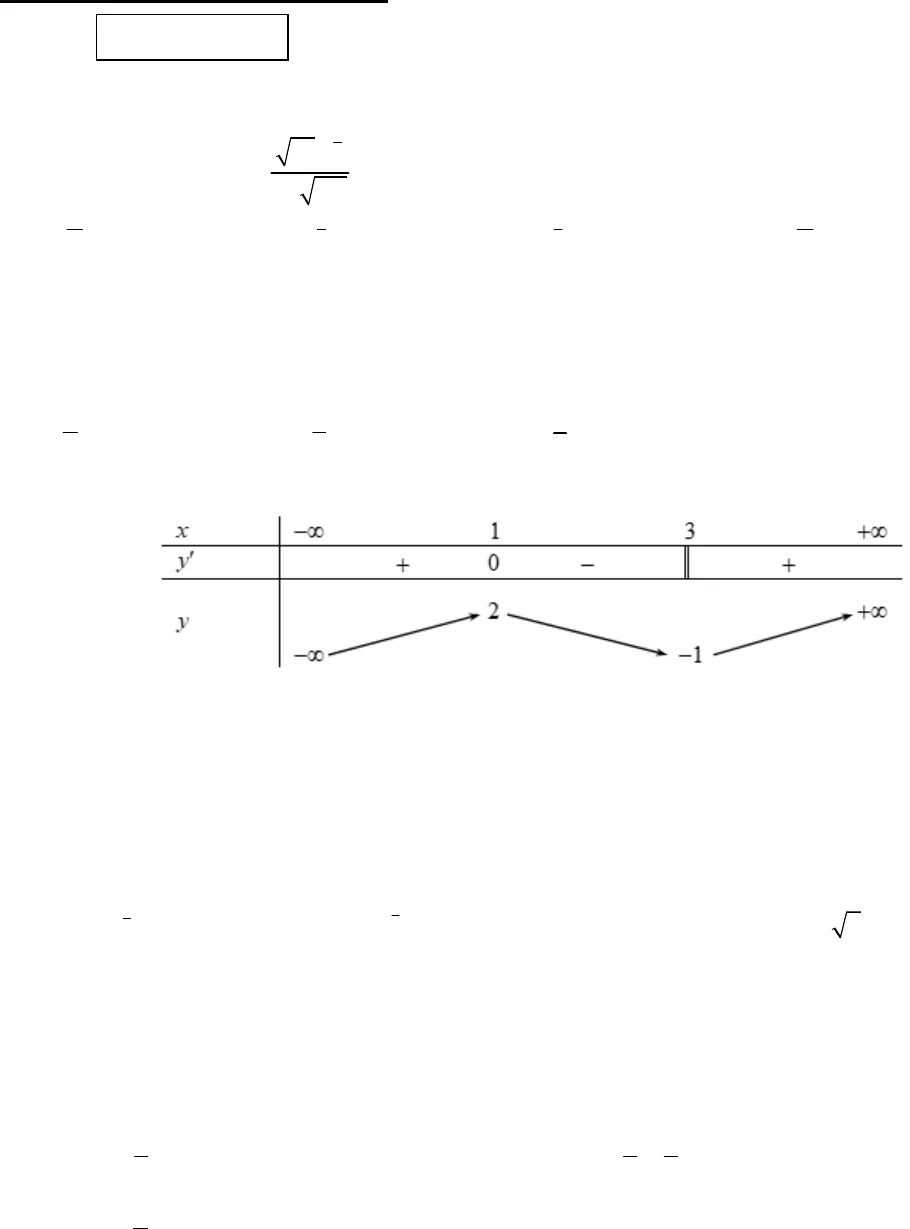Trang 1/6 – Mã đề thi 210SỞ GIÁO DỤC & ĐÀO TẠO THÁI BÌNHTRƯỜNG THPT CHUYÊN THÁI BÌNH ĐỀ THI THỬ THPTQG LẦN I – NĂM HỌC: 2019 – 2020MÔN TOÁNThời gian làm bài: 90 phút(50 câu trắc nghiệm)Họ và tên thí sinh: …….………………………..……………….. Lớp: …………. SBD: ………………..Câu 1: Rút gọn biểu thức 735374 2..a aAa avới0a. Khẳng định nào sau đây đúng? A.27A a. B. 27A a. C. 72A a. D. 72A a.Câu 2: Cho hàm số 2sin cosy x x . Đạo hàm của hàm số là:A.2cos sinx x . B.2cos siny x x  .C. 2cos siny x x . D.2cos siny x x . Câu 3: Hàm số nào trong bốn hàm số liệt kê ở dưới nghịch biến trên từng khoảng xác định của nó? A.2 1e2xy   . B. 13xy   C. 3exy   . D. 2017xy  . Câu 4: Cho hàm số  y f xliên tục trênvà có bảng biến thiên như sau:Khẳng định nào sau đây đúng?A. Hàm số đạt cực tiểu tại điểm 3x. B. Hàm số có giá trị nhỏ nhất trênbằng1. C. Hàm số có giá trị cực đại bằng 1. D. Hàm số chỉ có một điểm cực trị. Câu 5: Hình bát diện đều có bao nhiêu cạnh? A.16. B.8. C.24. D. 12.Câu 6: Trong các hàm số sau đây, hàm số nào xác định với mọi giá trị thực của x?A. 132 1y x . B.  1232 1y x . C.  31 2y x . D.  31 2y x .Câu 7: Công thức tính diện tích xung quanh của hình nón tròn xoay có bán kính đáy rvà độ dài đườngsinhllà:A. xqSrl. B.2xqSrl. C. xqSrl. D. 2xqSrlCâu 8: Cho các số thực dương ,a bvới1a . Tìm mệnh đề đúng trong các mệnh đề dưới đây.A. 21log log2aaab b. B.  21 1log log2 2aaab b .C. 21log log4aaab b. D.  2log 2 2 logaaab b .Câu 9: Cho hàm số ( )y f xcó đạo hàm trênvà’( ) 0 (0; )f x x   . Biết(1) 2020f. Khẳngđịnh nào dưới đây đúng?A.   2020 2022f f. B. (2018) (2020)f f.C.(0) 2020f. D. (2) (3) 4040f f .Câu 10: Cho hình chóp .S ABCcó, ,SA SB SCđôi một vuông góc. BiếtSA SB SC a  , tính thể tíchcủa khối chóp.S ABC.MÃ ĐỀ 210 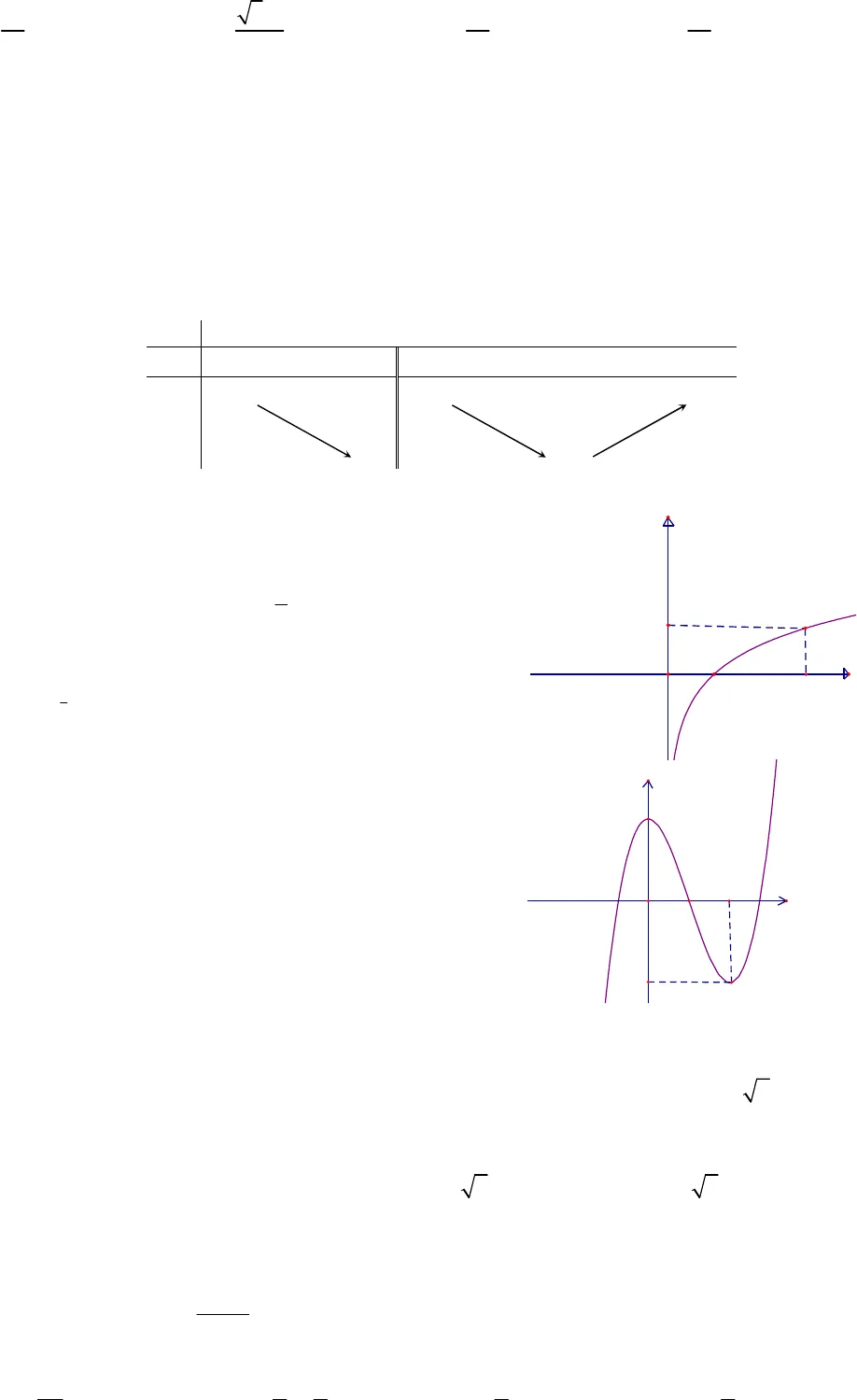Trang 2/6 – Mã đề thi 210A.36a. B. 334a. C. 32a. D. 33a. Câu 11: Tổng 0 1 2 2 3 33 3 3 … ( 1) .3n n nn n n n nS C C C C C      bằng:A.2nB. ( 2)nC. 4nD. 2nCâu 12: Cho 10 điểm phân biệt. Hỏi có thể lập được bao nhiêu vectơ khác 0mà điểm đầu và điểm cuốithuộc 10 điểm đã cho.A. 210C. B. 210A. C. 28A. D. 110A.Câu 13:Cho hàm số y f xcó bảng biến thiên như hình bên dưới. Hỏi đồ thị hàm số đã cho có tất cảbao nhiêu đường tiệm cận đứng và ngang?A. 3. B.1. C.2. D.4.Câu 14: Hàm số nào dưới đây có đồ thị như trong hình vẽ bên?A.2xy. B. 13xy   .C.13logy x . D. 3logy x . 01xy31Câu 15: Đường cong trong hình vẽ bên là đồ thị của hàm số nào trong các hàm số dưới đây?A.3 23 2y x x   .B.3 23 2y x x  . C. 33 2y x x  .D. 4 22 2y x x   .201xy2-2Câu 16: Hàm số 4 23y x x  có mấy điểm cực trị?A. 1. B. 2. C. 3. D. 0.Câu 17: Cho hình lập phương .ABCD A B C D   có diện tích mặt chéoACC A bằng22 2a. Thể tíchcủa khối lập phương.ABCD A B C D   là:A.3aB.32aC.32aD.32 2aCâu 18: Tìm số giao điểm của đồ thị hàm số 33 3y x x  và đường thẳngy x.A.1. B. 2. C. 3. D. 0.Câu 19. Cho hàm số 2 11xyxcó đồ thị Cvà đường thẳng: 2 3d y x . Đường thằngdcắt( )Ctạihai điểmAvàB. Tọa độ trung điểm của đoạnABlà:A.3; 62M   . B. 3 3;4 2M   . C. 3;02M   . D. 3;04M   .x12y 0y325 Trang 3/6 – Mã đề thi 210Câu 20: Hàm số  22log 2y x x nghịch biến trên khoảng nào sau đây?A. ;1. B.  ;0. C.  1;1. D.  0;.Câu 21: Hai đường tiệm cận của đồ thị hàm số 2 11xyxtạo với hai trục tọa độ một hình chữ nhật códiện tích bằng bao nhiêu? A. 2. B.1. C.3. D.4.Câu 22: Cho mặt cầu ( ; )S I Rvà mặt phẳng( )PcáchImột khoảng bằng2R. Khi đó thiết diện của( )Pvà Slà một đường tròn có bán kính bằng:A.R. B. 32R. C. 3RD.2RCâu 23: Gọi m,Mlần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số 112f x x x  trênđoạn 0;3. Tính tổng2S M m .A. 0S. B.32S . C.2S . D.4S.Câu 24: Hàm số: 3 23 9 7y x x x   đồng biến trên khoảng nào sau đây?A. 1;y . B. 5; 2 . C. ;1. D. 1;3.Câu 25: Viết phương trình tiếp tuyến của đồ thị 3( ) : 2 lnC y x x x tại điểm(1;2)M. A.7 9y x  . B. 3 4y x . C. 7 5y x . D. 3 1y x . Câu 26: Cho hình chóp .S ABCcó đáyABClà tam giác đều cạnha, cạnh bênSAvuông góc với đáy,SA a. Thể tích của khối chóp.S ABCbằng:A. 334a. B. 336a. C. 34a. D. 3312a.Câu 27: Hai anh em A sau Tết có 20 000 000đồng tiền mừng tuổi. Mẹ gửi ngân hàng cho hai anh emvới lãi suất0,5/tháng (sau mỗi tháng tiền lãi được nhập vào tiền gốc để tính lãi tháng sau). Hỏi sau1năm hai anh em được nhận bao nhiêu tiền biết trong một năm đó hai anh em không rút tiền lần nào (sốtiền được làm tròn đến hàng nghìn)?A.21 233 000đồng. B. 21 234 000đồng. C.21 235 000đồng. D.21 200 000đồng.Câu 28: Cho khối chóp .S ABCDcó thể tích bằng34a, đáy ABCD là hình bình hành. Gọi làMtrungđiểm của cạnhSD. Biết diện tích tam giác SAB bằng2.aTính khoảng cách từMtới mặt phẳng( )SAB.A.12a.B. 6 .aC. 3 .a D. 4 .aCâu 29: Cho avàblà các số thực dương khác1. Biếtrằng bất kì đường thẳng nào song song với trục tung màcắt các đồ thịlogay x , logby x và trục hoành lần lượt tạiA,BvàHphân biệt ta đều có3 4HA HB(hình vẽ bên dưới). Khẳng định nào sau đây là đúng?A.4 31a b.B.3 41a b.C. 3 4a b.D.4 3a b.Câu 30: Một hình trụ nội tiếp một hình lập phương cạnh a. Thể tích của khối trụ đó là: