Download.vn Học tập Lớp 12 Thi THPT Quốc Gia Toán
Bạn đang đọc: Các dạng toán về hàm ẩn liên quan đến tiệm cận của hàm số
Các dạng toán về hàm ẩn liên quan đến tiệm cận của hàm số Tài liệu ôn tập môn Toán lớp 12
Giới thiệu Tải về Bình luận
- 1
Mua tài khoản Download Pro để trải nghiệm website Download.vn KHÔNG quảng cáo & tải File cực nhanh chỉ từ 79.000đ. Tìm hiểu thêm Mua ngay
Với mong muốn đem đến cho quý thầy cô cùng các bạn học sinh lớp 12 có thêm nhiều tài liệu học tập chương trình Giải tích 12 chương 1 và ôn tập thi THPT Quốc gia 2020, Download.vn xin giới thiệu tài liệu Các dạng toán về hàm ẩn liên quan đến tiệm cận của hàm số.
Đây là tài liệu vô cùng hữu ích, bao gồm 95 trang tuyển chọn các bài toán trắc nghiệm có đáp án và lời giải chi tiết chủ đề bài toán hàm ẩn liên quan đến tiệm cận của hàm số. Đây là dạng toán được bắt gặp khá thường xuyên trong các đề thi thử THPT Quốc gia môn Toán của các trường THPT và cơ sở GD&ĐT trên toàn quốc. Nội dung chi tiết mời các bạn cùng tham khảo và tải tài liệu tại đây.
Các dạng toán về hàm ẩn liên quan đến tiệm cận của hàm số
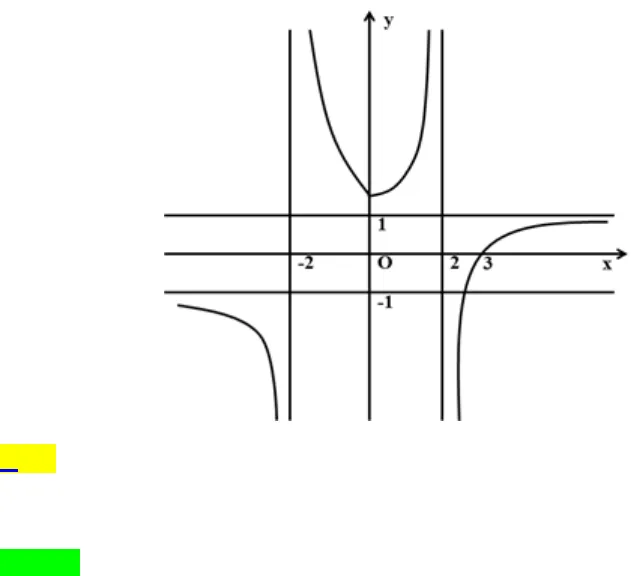Phần 1: Biết đồ thị hàm số ( )y fx=Dạng 1: Biết đồ thị của hàm số( )y fx=, tìm tiệm cận đứng, tiệm cận ngang của đồ thị hàm số ( )y fx=, trong bài toán không chứa tham số.Câu 1. Cho hàm số ( )y fx=có đồ thị như hình vẽ. Đồ thị hàm số đã cho có bao nhiêu đường tiệm cận? A.4. B. 2. C. 1. D. 3.Lời giải Chọn A Từ đồ thị hàm số ta thấy:( )lim 1xfx→−∞= −nên đường thẳng1y= −là một đường tiệm cận ngang.( )lim 1xfx→+∞=nên đường thẳng1y =là một đường tiệm cận ngang.Đồ thị hàm số có hai tiệm cận ngang là 1y = ±.Tương tự ( )2limxfx+→−= +∞và()2limxfx−→−= −∞nên đường thẳng2x = −là đường tiệm cậnđứng. ( )2limxfx−→= +∞và và( )2limxfx+→= −∞nên đường thẳng2x = −là đường tiệm cậnđứng. Đồ thị hàm số có hai tiệm cận đứng là 2x = ±.Các dạng toán về hàm ẩn liên quan đến tiệm cận của hàm số
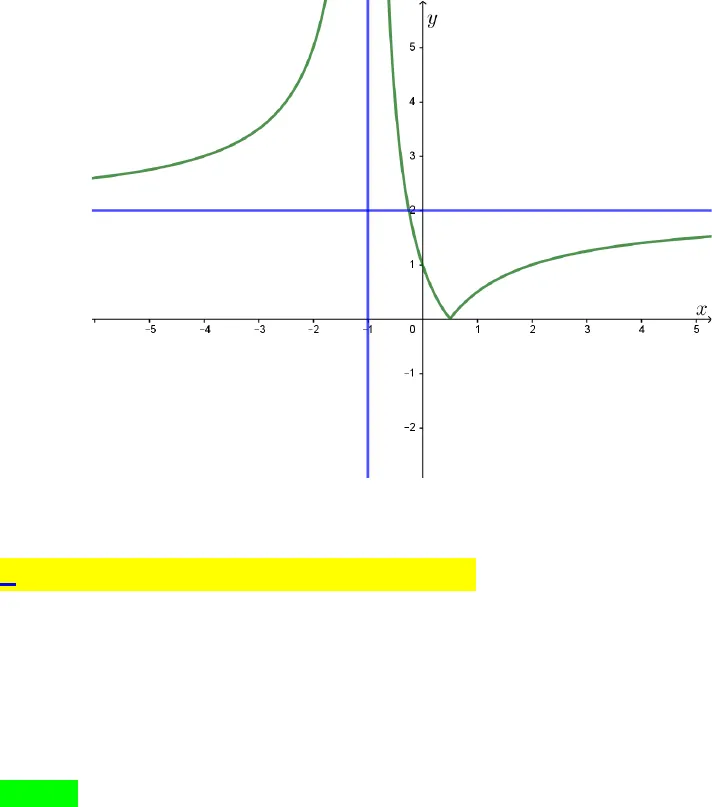Vậy đồ thị hàm số có 4 đường tiệm cận.Câu 1. Cho hàm số ( )y fx=có đồ thị như hình vẽ. Phương trình đường tiệm cận đứng và đường tiệm cận ngang của đồ thị hàm số là A. Tiệm cận đứng 1x =, tiệm cận ngang2y =.B. Tiệm cận đứng 1x = −, tiệm cận ngang2y =.C. Tiệm cận đứng 1x =, tiệm cận ngang2y= −.D. Tiệm cận đứng 1x = −, tiệm cận ngang2y = −.Lời giảiChọn B Dựa vào đồ thị ta có( )( )1limxfx−→−= +∞và( )( ) 1limxfx+→−= +∞nên đường thẳng1x = −là tiệm cậnđứng của đồ thị hàm số ( )y fx=. ( )lim 2xfx→−∞=và( )+lim 2xfx→∞=nên đường thẳng 2y =là tiệm cận ngang của đồthị hàm số ( )y fx=. Câu 2. Cho hàm số ( )y fx=có đồ thị như hình vẽ. Phương trình đường tiệm cận đứng và đường tiệm cận ngang của đồ thị hàm số là 
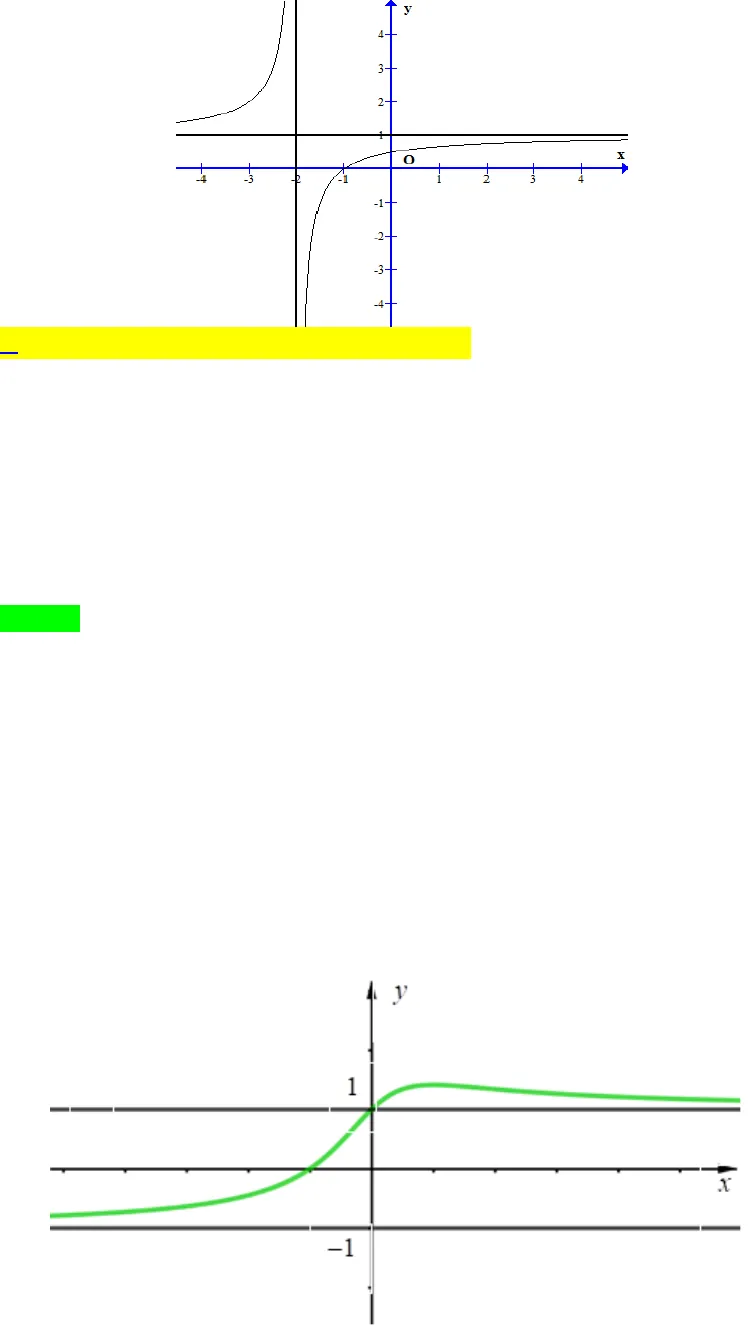A. Tiệm cận đứng 2x = −, tiệm cận ngang1y =.B. Tiệm cận đứng 2x =, tiệm cận ngang1y = −.C. Tiệm cận đứng 1x=, tiệm cận ngang2y= −.D. Tiệm cận đứng 1x = −, tiệm cận ngang2y =.Lời giảiChọn A Dựa vào đồ thị ta có()( )2limxfx−→−= +∞và( )( )2limxfx+→−= −∞nên đường thẳng 2x = −là tiệm cận đứngcủa đồ thị hàm số( )y fx=.+)( )lim 1xfx→−∞=và( )lim 1xfx→+∞=nên đường thẳng1y =là tiệm cận ngang đứngcủa đồ thị hàm số( )y fx=.Câu 3. Cho hàm số ( )y fx=có đồ thị như hình vẽ dưới đây.Số đường tiệm cận ngang của đồ thị hàm số là 