Download.vn Học tập Lớp 12 Thi THPT Quốc Gia Toán
Bạn đang đọc: Các phương pháp tính thể tích khối đa diện
Các phương pháp tính thể tích khối đa diện Tài liệu ôn tập môn Toán lớp 12
Giới thiệu Tải về Bình luận
- 1
Mua tài khoản Download Pro để trải nghiệm website Download.vn KHÔNG quảng cáo & tải File cực nhanh chỉ từ 79.000đ. Tìm hiểu thêm Mua ngay
Mời quý thầy cô giáo cùng các bạn học sinh lớp 12 cùng tham khảo tài liệu Các phương pháp tính thể tích khối đa diện được chúng tôi tổng hợp và đăng tải ngay sau đây.
Đây là tài liệu cực kì hữu ích, gồm 34 trang hướng dẫn các phương pháp tính thể tích khối đa diện và các bài tập vận dụng. Hy vọng với tài liệu này các bạn học sinh có thêm nhiều tài liệu tham khảo, củng cố nắm vững kiến thức thể tích khối đa diện để đạt được kết quả cao trong các bài kiểm tra, bài thi THPT Quốc gia sắp tới. Đồng thời đây cũng là tư liệu tham khảo dành cho các giáo viên giảng dạy. Nội dung chi tiết mời bạn đọc cùng tham khảo và tải tài liệu tại đây.
Các phương pháp tính thể tích khối đa diện
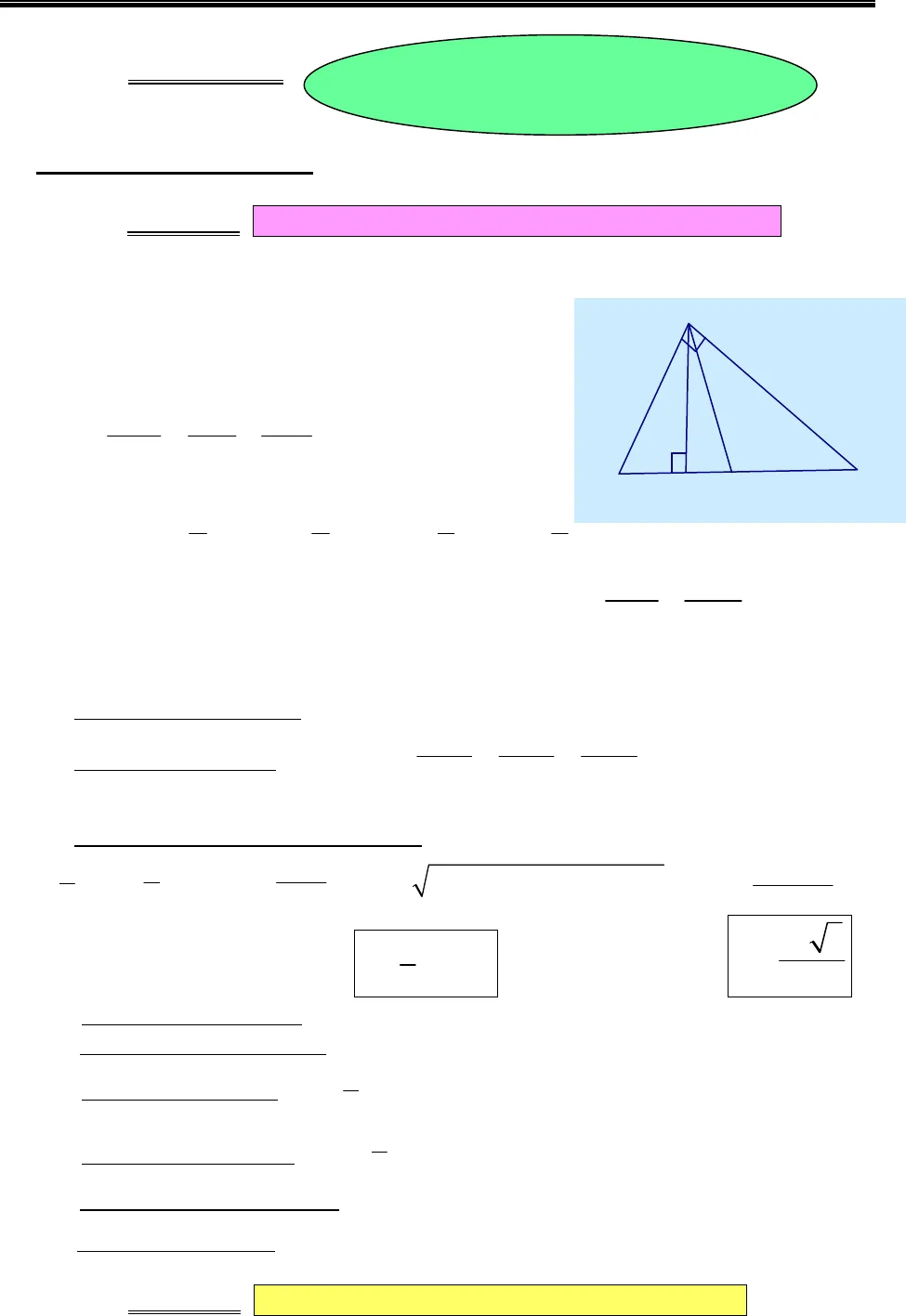 Thể tích khối đa diện – www.mathvn.comhttp://book.mathvn.com 1cbaMHCBACHUYÊN ĐỀ: PHƯƠNG PHÁP LUYỆN TẬP THỂ TÍCH KHỐI ĐA DIỆN I. Ôn tập kiến thức cơ bản: ÔN TẬP 1. KIẾN THỨC CƠ BẢN HÌNH HỌC LỚP 9 – 10 1. Hệ thức lượng trong tam giác vuông : cho ABCDvuông ở A ta có : a) Định lý Pitago :2 2 2BC AB AC= +b) CBCHCABCBHBA .;.22==c) AB. AC = BC. AHd) 222111ACABAH+=e) BC = 2AMf) sin , os , tan ,cotb c b cB c B B Ba a c b= = = =g) b = a. sinB = a.cosC, c = a. sinC = a.cosB, a =sin cosb bB C=,b = c. tanB = c.cot C2.Hệ thức lượng trong tam giác thường: * Định lý hàm số Côsin: a2= b2+ c2- 2bc.cosA* Định lý hàm số Sin: 2sin sin sina b cRA B C= = =3. Các công thức tính diện tích. a/ Công thức tính diện tích tam giác: 12S=a.ha=1 . .. sin . .( )( )( )2 4a b ca b C p r p p a p b p cR= = = – – -với2a b cp+ +=Đặc biệt :*ABCDvuông ở A :1.2S AB AC=,*ABCDđều cạnh a:234aS =b/ Diện tích hình vuông : S = cạnh x cạnh c/ Diện tích hình chữ nhật : S = dài x rộngd/ Diên tích hình thoi : S =12(chéo dài x chéo ngắn) d/ Diện tích hình thang : 12S=(đáy lớn + đáy nhỏ) x chiều cao e/ Diện tích hình bình hành : S = đáy x chiều cao f/ Diện tích hình tròn :2S .Rp=ÔN TẬP 2 KIẾN THỨC CƠ BẢN HÌNH HỌC LỚP 11
Thể tích khối đa diện – www.mathvn.comhttp://book.mathvn.com 1cbaMHCBACHUYÊN ĐỀ: PHƯƠNG PHÁP LUYỆN TẬP THỂ TÍCH KHỐI ĐA DIỆN I. Ôn tập kiến thức cơ bản: ÔN TẬP 1. KIẾN THỨC CƠ BẢN HÌNH HỌC LỚP 9 – 10 1. Hệ thức lượng trong tam giác vuông : cho ABCDvuông ở A ta có : a) Định lý Pitago :2 2 2BC AB AC= +b) CBCHCABCBHBA .;.22==c) AB. AC = BC. AHd) 222111ACABAH+=e) BC = 2AMf) sin , os , tan ,cotb c b cB c B B Ba a c b= = = =g) b = a. sinB = a.cosC, c = a. sinC = a.cosB, a =sin cosb bB C=,b = c. tanB = c.cot C2.Hệ thức lượng trong tam giác thường: * Định lý hàm số Côsin: a2= b2+ c2- 2bc.cosA* Định lý hàm số Sin: 2sin sin sina b cRA B C= = =3. Các công thức tính diện tích. a/ Công thức tính diện tích tam giác: 12S=a.ha=1 . .. sin . .( )( )( )2 4a b ca b C p r p p a p b p cR= = = – – -với2a b cp+ +=Đặc biệt :*ABCDvuông ở A :1.2S AB AC=,*ABCDđều cạnh a:234aS =b/ Diện tích hình vuông : S = cạnh x cạnh c/ Diện tích hình chữ nhật : S = dài x rộngd/ Diên tích hình thoi : S =12(chéo dài x chéo ngắn) d/ Diện tích hình thang : 12S=(đáy lớn + đáy nhỏ) x chiều cao e/ Diện tích hình bình hành : S = đáy x chiều cao f/ Diện tích hình tròn :2S .Rp=ÔN TẬP 2 KIẾN THỨC CƠ BẢN HÌNH HỌC LỚP 11 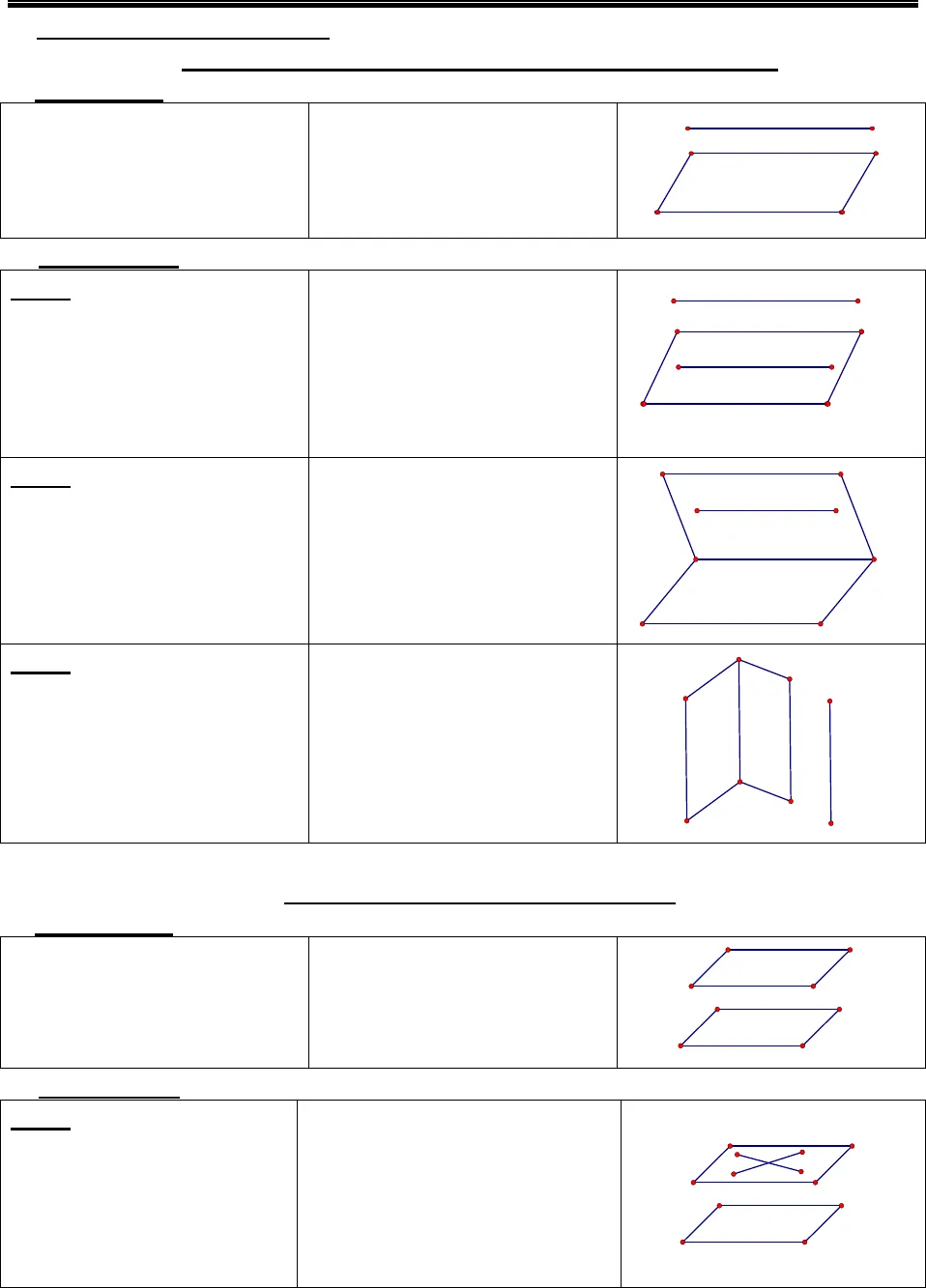 Thể tích khối đa diện – www.mathvn.comhttp://book.mathvn.com 2A.QUAN HỆ SONG SONG§1.ĐƯỜNG THẲNG VÀ MẶT PHẲNG SONG SONG I. Định nghĩa:Đường thẳng và mặtphẳng gọi là song songvới nhau nếu chúng không có điểm nào chung.a//(P) a (P)Û Ç =Æa(P)II.Các định lý: ĐL1:Nếu đường thẳng d không nằm trên mp(P) vàsong song với đường thẳng a nằm trên mp(P) thì đường thẳng d song song với mp(P) d (P)d/ /a d/ /(P)a (P)ìËïÞíïÌîda(P)ĐL2: Nếu đường thẳng a song song với mp(P) thì mọi mp(Q) chứa a mà cắt mp(P) thì cắt theo giao tuyến song song với a. a/ /(P)a (Q) d/ /a(P) (Q) dìïÌ ÞíïÇ =îda(Q)(P)ĐL3: Nếu hai mặt phẳng cắt nhau cùng song songvới một đường thẳng thìgiao tuyến của chúng song song với đường thẳng đó.(P) (Q) d(P)/ /a d/ /a(Q)/ /aìÇ =ïÞíïîadQP§2.HAI MẶT PHẲNG SONG SONG I. Định nghĩa:Hai mặt phẳng được gọi là song song với nhau nếu chúng không có điểm nào chung.(P)/ /(Q) (P) (Q)Û Ç =ÆQPII.Các định lý:ĐL1: Nếu mp(P) chứa hai đường thẳng a, b cắtnhau và cùng song songvới mặt phẳng (Q) thì(P) và (Q) song song với nhau.a,b (P)a b I (P)/ /(Q)a/ /(Q),b/ /(Q)ìÌïÇ = ÞíïîIbaQP
Thể tích khối đa diện – www.mathvn.comhttp://book.mathvn.com 2A.QUAN HỆ SONG SONG§1.ĐƯỜNG THẲNG VÀ MẶT PHẲNG SONG SONG I. Định nghĩa:Đường thẳng và mặtphẳng gọi là song songvới nhau nếu chúng không có điểm nào chung.a//(P) a (P)Û Ç =Æa(P)II.Các định lý: ĐL1:Nếu đường thẳng d không nằm trên mp(P) vàsong song với đường thẳng a nằm trên mp(P) thì đường thẳng d song song với mp(P) d (P)d/ /a d/ /(P)a (P)ìËïÞíïÌîda(P)ĐL2: Nếu đường thẳng a song song với mp(P) thì mọi mp(Q) chứa a mà cắt mp(P) thì cắt theo giao tuyến song song với a. a/ /(P)a (Q) d/ /a(P) (Q) dìïÌ ÞíïÇ =îda(Q)(P)ĐL3: Nếu hai mặt phẳng cắt nhau cùng song songvới một đường thẳng thìgiao tuyến của chúng song song với đường thẳng đó.(P) (Q) d(P)/ /a d/ /a(Q)/ /aìÇ =ïÞíïîadQP§2.HAI MẶT PHẲNG SONG SONG I. Định nghĩa:Hai mặt phẳng được gọi là song song với nhau nếu chúng không có điểm nào chung.(P)/ /(Q) (P) (Q)Û Ç =ÆQPII.Các định lý:ĐL1: Nếu mp(P) chứa hai đường thẳng a, b cắtnhau và cùng song songvới mặt phẳng (Q) thì(P) và (Q) song song với nhau.a,b (P)a b I (P)/ /(Q)a/ /(Q),b/ /(Q)ìÌïÇ = ÞíïîIbaQP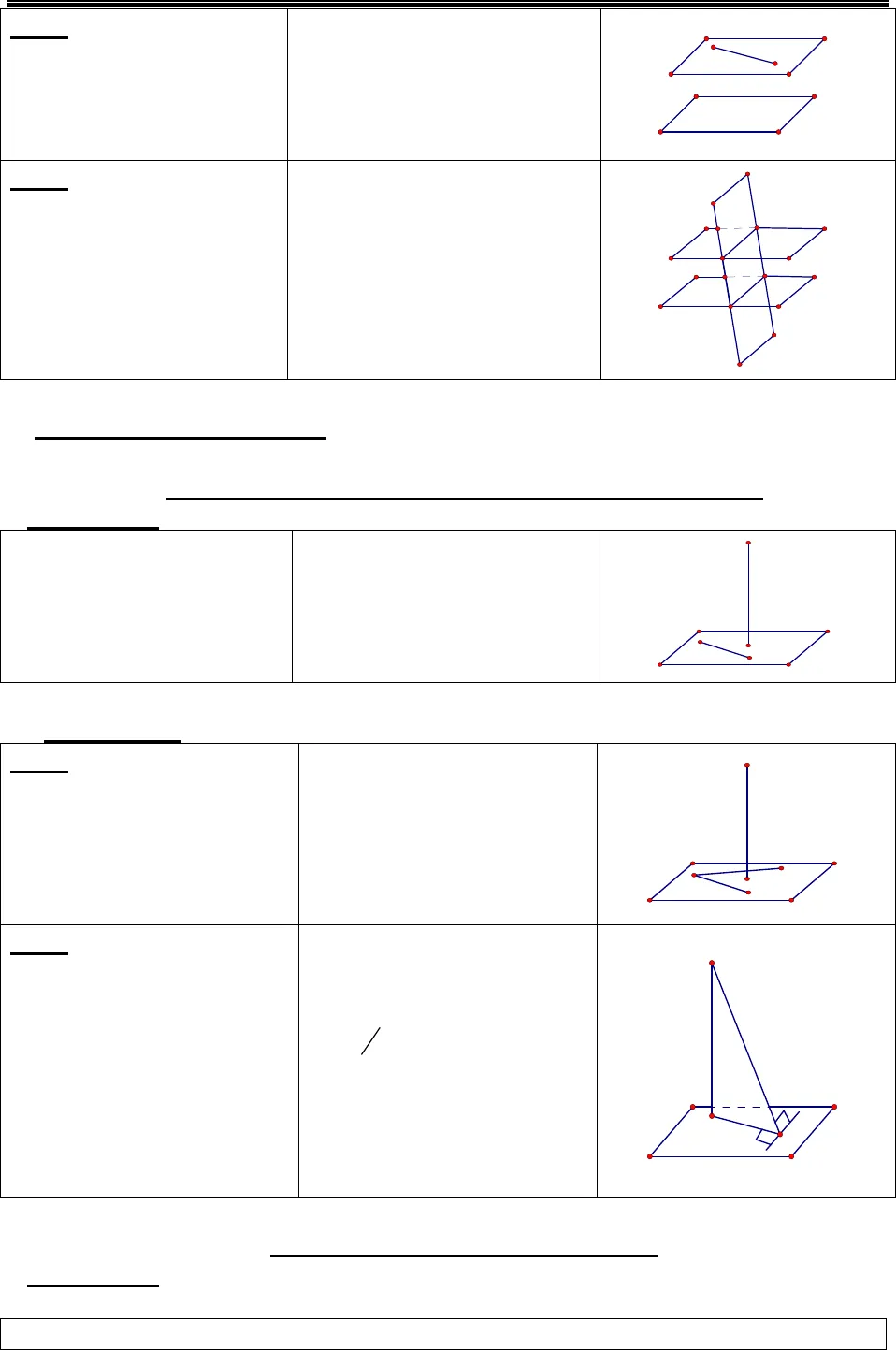 Thể tích khối đa diện – www.mathvn.comhttp://book.mathvn.com 3ĐL2: Nếu một đường thẳng nằm một trong hai mặt phẳng song song thìsong song với mặt phẳng kia.(P)/ /(Q)a / /(Q)a (P)ìÞíÌîaQPĐL3: Nếu hai mặt phẳng (P) và (Q) song song thìmọi mặt phẳng (R) đãcắt (P) thì phải cắt (Q) vàcác giao tuyến của chúng song song.(P) / /(Q)(R) (P) a a / /b(R) (Q) bìïÇ = ÞíïÇ =îbaRQP B.QUAN HỆ VUÔNG GÓC §1.ĐƯỜNG THẲNG VUÔNG GÓC VỚI MẶT PHẲNG I.Định nghĩa: Một đường thẳng được gọi là vuông góc với một mặt phẳng nếu nó vuông góc với mọi đường thẳng nằm trên mặt phẳng đó. a mp(P) a c, c (P)^ Û ^ “ ÌPcaII. Các định lý:ĐL1: Nếu đường thẳng d vuông góc với hai đường thẳng cắt nhau a và bcùng nằm trong mp(P) thì đường thẳng d vuông gócvới mp(P). d a,d ba,b mp(P) d mp(P)a,b caét nhauì^ ^ïÌ Þ ^íïîdabPĐL2: (Ba đường vuông góc) Cho đường thẳng a không vuông góc với mp(P) và đường thẳng bnằm trong (P). Khi đó, điều kiện cần và đủ để bvuông góc với a là bvuông góc với hình chiếu a’ của a trên (P).a mp(P),b mp(P)b a b a‘^ Ì^ Û ^a‘abP§2.HAI MẶT PHẲNG VUÔNG GÓC I.Định nghĩa: Hai mặt phẳng được gọi là vuông góc với nhau nếu góc giữa chúng bằng 900.
Thể tích khối đa diện – www.mathvn.comhttp://book.mathvn.com 3ĐL2: Nếu một đường thẳng nằm một trong hai mặt phẳng song song thìsong song với mặt phẳng kia.(P)/ /(Q)a / /(Q)a (P)ìÞíÌîaQPĐL3: Nếu hai mặt phẳng (P) và (Q) song song thìmọi mặt phẳng (R) đãcắt (P) thì phải cắt (Q) vàcác giao tuyến của chúng song song.(P) / /(Q)(R) (P) a a / /b(R) (Q) bìïÇ = ÞíïÇ =îbaRQP B.QUAN HỆ VUÔNG GÓC §1.ĐƯỜNG THẲNG VUÔNG GÓC VỚI MẶT PHẲNG I.Định nghĩa: Một đường thẳng được gọi là vuông góc với một mặt phẳng nếu nó vuông góc với mọi đường thẳng nằm trên mặt phẳng đó. a mp(P) a c, c (P)^ Û ^ “ ÌPcaII. Các định lý:ĐL1: Nếu đường thẳng d vuông góc với hai đường thẳng cắt nhau a và bcùng nằm trong mp(P) thì đường thẳng d vuông gócvới mp(P). d a,d ba,b mp(P) d mp(P)a,b caét nhauì^ ^ïÌ Þ ^íïîdabPĐL2: (Ba đường vuông góc) Cho đường thẳng a không vuông góc với mp(P) và đường thẳng bnằm trong (P). Khi đó, điều kiện cần và đủ để bvuông góc với a là bvuông góc với hình chiếu a’ của a trên (P).a mp(P),b mp(P)b a b a‘^ Ì^ Û ^a‘abP§2.HAI MẶT PHẲNG VUÔNG GÓC I.Định nghĩa: Hai mặt phẳng được gọi là vuông góc với nhau nếu góc giữa chúng bằng 900.
