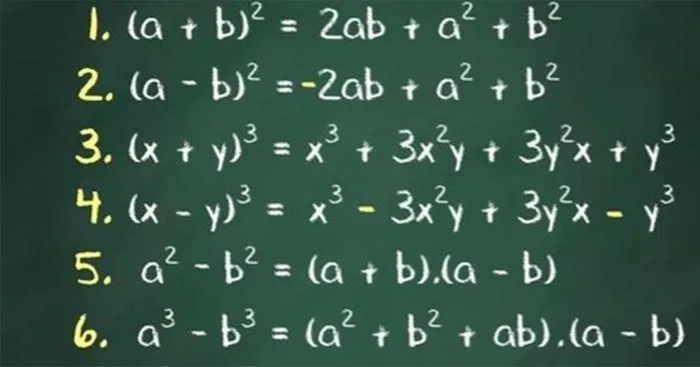Cách sử dụng hằng đẳng thức để rút gọn biểu thức là một trong những dạng toán trọng tâm thường xuất hiện trong các bài kiểm tra, bài thi học kì môn Toán lớp 8.
Bạn đang đọc: Cách sử dụng hằng đẳng thức để rút gọn biểu thức
Cách rút gọn biểu thức sử dụng hằng đẳng thức tổng hợp toàn bộ kiến thức về cách rút gọn kèm theo một số ví dụ minh họa và bài tập tự luyện. Thông qua tài liệu này giúp học sinh củng cố, nắm vững chắc kiến thức nền tảng, vận dụng với các bài tập cơ bản để đạt được kết quả cao trong kì thi sắp tới. Bên cạnh đó các bạn xem thêm tài liệu Cách tính giá trị biểu thức lớp 8.
Cách sử dụng hằng đẳng thức để rút gọn biểu thức
I. Cách sử dụng hằng đẳng thức để rút gọn biểu thức
Với A, B là các biểu thức tùy ý, ta có:
1.Bình phương của một tổng
(A + B)2 = A2 + 2AB + B2
2.Bình phương của một hiệu
(A – B)2 = A2 – 2AB + B2
3.Hiệu hai bình phương
A2 – B2 = (A – B)(A + B)
4.Lập phương của một tổng
(A + B)3 = A3 + 3A2B + 3AB2 + B3
5.Lập phương của một hiệu.
(A – B)3 = A3 – 3A2B + 3AB2 – B3
6.Tổng hai lập phương
A3 + B3 = (A + B)(A2 – AB + B2)
7.Hiệu hai lập phương
A3 – B3 = (A – B)(A2 + AB + B2)
Chú ý: Ta quy ước A2 + AB + B2 là bình phương thiếu của tổng A + B.
II. Ví dụ sử dụng hằng đẳng thức để rút gọn biểu thức
Ví dụ 1. Tính (a + 3)2
A. a2 + 6a + 9 B. a2 + 3a + 9 C. a2+ 6a + 3 D. a2 +3a + 3
Gợi ý đáp án
(a + 3)2 = a2 + 2.a.3 + 32 = a2 + 6a + 9
Chọn A.
Ví dụ 2. Viết biểu thức x2 + 4x + 4 dưới dạng bình phương của một tổng.
A. (x+ 4)2 B. (x+2)2 C. (x+ 1)2 D. (2x +1)2
Gợi ý đáp án
Ta có x2 + 4x + 4 = x2 + 2.x.2 + 22 = (x + 2)2.
Chọn B.
Ví dụ 3. Tính (2x – 3y)2
A. 4x2 – 12xy + y2 B. 4x2 + 12xy – 9y2 C. 4x2 – 6xy + 9y2 D. 4x2 – 12xy + 9y2
Gợi ý đáp án
Ta có:
(2x – 3y)2 = (2x)2 – 2.2x.3x + (3y)2
= 4x2 – 12xy + 9y2
Chọn D.
Ví dụ 4. Tính (2x – 3y)3
A. 8x3 – 36x2y + 54xy2 – 27y3
B. 8x3 – 36x2y + 27xy2 – 27y3
C. 8x3 – 54x2y + 36xy2 – 27y3
D. 8x3 – 27x2y + 54xy2 – 36y3
Gợi ý đáp án
Ta có:
(2x – 3y)3 = (2x)3 – 3.(2x)2.3y + 3.2x.(3y)2 – (3y)3
= 8x3 – 36x2y + 54xy2 – 27y3
Chọn A.
III. Bài tập sử dụng hằng đẳng thức để rút gọn
Câu 1. Tính ( 5x -y)2
A. 10x2 – 10xy + y2
B. 25x2 – 5xy + y2
C. 25x2 – 10xy + y2
D. x2 + 10xy + y2
Câu 2. Viết biểu thức 36x2 – 24xy + 4y2 dưới dạng bình phương của một hiệu.
A.( 2x- 2y)2
B. (2x – 6y)2
C. (6x – 6y)2
D. ( 6x- 2y)2
Câu 3. Đưa biểu thức sau về dạng tích 81 – 25x2
A. (3 – 5x). (3+ 5x)
B. (9+ 5x). (9- x)
C. (9+ 5x).(9- 5x)
D. Đáp án khác
Câu 4 . Tính 56. 64.
A. 3600
B. 2880
C. 3248
D. 3584
Câu 5. Viết biểu thức x3 + 6x2 +12x + 8 dưới dạng lập phương của một tổng.
A. (x+ 1)3
B. (x+ 2)3
C. (2x +1)3
D. (2x +2)3
Câu 6. Khai triển ( 4x – y)3
A. 64x3 – 48x2y + 12xy2 – y3
B. 64x3 – 12x2y + 48xy2 – y3
C. 12x3 – 48x2y + 12xy2 – y3
D. Đáp án khác
Câu 7. Viết biểu thức x3 – 6x2y + 12xy2 – 8y3 dưới dạng lập phương của một hiệu.
A. (x – 2y)3
B. (2y – x)3
C. ( 2x – 2y)3
D. (x – 4y)3
Câu 8. Viết biểu thức (2x+ 4). (4x2 – 8x +16 ) dưới dạng tổng hai lập phương.
A. 8x3 + 32
B. 8x3 + 12
C. 8x3 + 64
D. 6x3 +12
Câu 9. Viết biểu thức (x – 2y)(x2 + 2xy + 4y2) dưới dạng hiệu hai lập phương
A.x3 – 8y3
B. x3 – 6y3
C. 8x3 – y3
D. 2x3 – 4y3