Download.vn Học tập Lớp 12 Thi THPT Quốc Gia

Bạn đang đọc: Chuyên đề bảng biến thiên và đồ thị hàm số

Chuyên đề bảng biến thiên và đồ thị hàm số Tài liệu ôn thi THPT Quốc gia 2019

Giới thiệu Tải về Bình luận

• 1

Mua tài khoản Download Pro để trải nghiệm website Download.vn KHÔNG quảng cáo & tải File cực nhanh chỉ từ 79.000đ. Tìm hiểu thêm Mua ngay

Chuyên đề bảng biến thiên và đồ thị hàm số là tài liệu cực kì hữu ích mà Download.vn muốn giới thiệu đến các bạn học sinh lớp 12 cùng tham khảo.

Tài liệu gồm 150 trang được biên soạn bởi thầy Đặng Việt Đông, hướng dẫn giải các dạng toán thuộc chuyên đề bảng biến thiên và đồ thị hàm số trong chương trình Giải tích 12 chương 1: ứng dụng đạo hàm để khảo sát và vẽ đồ thị hàm số. Trong mỗi dạng toán, tài liệu giới thiệu lý thuyết cần nắm, phân dạng, hướng dẫn giải và các bài tập trắc nghiệm có đáp án và lời giải chi tiết. Nội dung chi tiết, mời các bạn cùng tham khảo và tải tài liệu tại đây.

Chuyên đề bảng biến thiên và đồ thị hàm số

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Bản biến thiên và Đồ thị hàm số File Word liên hệ: 0978064165 – Email: [email protected] Trang 1Facebook: https://www.facebook.com/dongpay MỤC LỤC BẢNG BIẾN THIÊN VÀ ĐỒ THỊ HÀM SỐ …………..………..………..………..…………..………..………..….. 0A – KIẾN THỨC CHUNG …..………..…………..………..………..………..………..…………..……..…………..……. 2B – CÁC DẠNG BÀI TẬP ….………..…………..……..…………..………..………..…………..………..………..…….. 7CHỦ ĐỀ 1: BẢNG BIẾN THIÊN …..………..…………..………..………..………..………..…………..……..………. 7 DẠNG 1: NHẬN DẠNG BBT ….……..…………..………..………..………..………..…………..………..……….... 7 DẠNG 2: BBT VỚI SỰ ĐƠN ĐIỆU CỦA HÀM SỐ ..…..…………..………..………..………..………..…….. 9 DẠNG 3: BBT VỚI CỰC TRỊ HÀM SỐ ..……..………..………..………..…………..……..…………..………. 12 DẠNG 4: BBT VỚI GTLN, GTNN CỦA HÀM SỐ ….………..………..………..………..…………..………. 14 DẠNG 5: BBT VỚI TIỆM CẬN CỦA ĐỒ THỊ HÀM SỐ ….……..………..………..…………..………..… 15 CHỦ ĐỀ 2: ĐỒ THỊ HÀM SỐ ..………..………..………..………..…………..……..…………..………..………..….. 18 DẠNG 1: ĐỒ THỊ VỚI SỰ ĐƠN ĐIỆU CỦA HÀM SỐ ..………..…………..………..………..………….... 18 DẠNG 2: ĐỒ THỊ VỚI CỰC TRỊ HÀM SỐ ...………..…………..……..…………..………..………..……….. 20 DẠNG 3: ĐỒ THỊ VỚI GTLN, GTNN CỦA HÀM SỐ …..………..…………..………..………..………..… 23 DẠNG 4: ĐỒ THỊ VỚI TIỆM CẬN CỦA ĐỒ THỊ HÀM SỐ …..………..…………..………..………..…. 25 DẠNG 5: NHẬN DẠNG ĐỒ THỊ CỦA CÁC HÀM SỐ …..………..…………..………..………..……….... 26 DẠNG 6: XÉT DẤU CÁC HỆ SỐ DỰA VÀO BBT VÀ ĐỒ THỊ…..………..…………..……..………… 30 DẠNG 7: XÉT SỰ TƯƠNG GIAO BẰNG BBT VÀ ĐỒ THỊ ..…..…………..………..………..…………. 38 STG SỬ DỤNG BẢNG BIẾN THIÊN ..………..………..………..………..…………..………..………..……. 38 STG SỬ DỤNG ĐỒ THỊ HÀM SỐ ...………..…………..………..………..…………..……..…………..……. 41 DẠNG 8: ĐỒ THỊ HÀM TRỊ TUYỆT ĐỐI ..…………..………..………..…………..………..………..………. 46 DẠNG 9: XÉT SỰ TƯƠNG GIAO VỚI BBT VÀ ĐỒ THỊ HÀM CHỨA TRỊ TUYỆT ĐỐI .…... 50 STG SỬ DỤNG BẢNG BIẾN THIÊN ..………..………..………..………..…………..………..………..……. 50 STG SỬ DỤNG ĐỒ THỊ HÀM SỐ .……..…………..………..………..………..………..…………..……….... 52 C – HƯỚNG DẪN GIẢI …...…………..………..………..………..………..…………..………..………..………..……. 60 ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Bản biến thiên và Đồ thị hàm số File Word liên hệ: 0978064165 – Email: [email protected] Trang 2Facebook: https://www.facebook.com/dongpay BẢNG BIẾN THIÊN VÀ ĐỒ THỊ HÀM SỐ A – KIẾN THỨC CHUNG1 – TÍNH ĐƠN ĐIỆU- Đối với bảng biến thiên nhìn vào dòng của y nếu thấy hướng mũi tên đi lên (đi xuống) thì hàm số đồng biến( nghịch biến). Để tìm xem đồng biến nghịch biến trên khoảng nào thì nhìn lên dòng của biến xtương ứng. – Đối với đồ thị hàm số:Theo hướng tăng dần của biến x nếu đồ thị đi lên (đi xuống) thì hàm số đồng biến( nghịch biến).2 – CỰC TRỊ – Đối với bảng biến thiên nhìn vào dòng của y nếu thấy tại điểm đó hàm số thay đổi tính chất từ đồng biến sang nghịch biến hoặc nhìn sang dòng y’ thấy dấu y’ đổi từ + sang – thì đó là điểm cực đại ngược lạ là điểm cực tiểu. – Đối với đồ thị hàm số: Nếu đồ thị đổi hướng từ đi lên sang đi xuống thì đó là điểm cưc đại ngựơc lại là cực tiểu. – Khi nói đến cực trị hàm số chú ý phân biệt 3 khái niệm + Điểm cực trị của hàm số + Giá trị cực trị của hàm số: y + Điểm cực trị của đồ thị hàm số: x,y 3 – TIỆM CẬN (GIỚI HẠN) – Nhìn vào bảng biến thiên hoặc đồ thị nếu : +Nếu( )x x   màoy ythìlimyoxy(limy )oxyhayoy ylà đường tiệm cận ngang của đồ thị hàm số.+Nếu( )o ox x x x   mà( )y y   thìlimyox x (limy )ox x hayox xlà đường tiệm cận đứng của đồ thị hàm số.4 – GIÁ TRỊ LỚN NHẤT, NHỎ NHẤT.– Nhìn vào bảng biến thiên hoặc đồ thị để tìm được hai số m, M sao cho: m y M + Nếu tồn tạiox Dđể ( )of x mthì min ( )x Df x m+ Nếu tồn tạiox Dđể ( )of x Mthì ( )x Dmax f x M5 – ĐỒ THỊ HÀM SỐHàm số bậc ba3 2y ax bx cx d   1. Tập xác định: D2. Đạo hàm: 2′ 3 2y ax bx c  ,23b ac   0 : Hàm số có 2 cực trị. 0 : Hàm số luôn tăng hoặc luôn giảm trên .3. Đạo hàm cấp 2:‘‘ 6 2y ax b , ‘‘ 03by xa    3bxa là hoành độ điểm uốn, đồ thị nhận điểm uốn làm tâm đối xứng. 4. Giới hạn: Nếu 0athì: lim ; limx xy y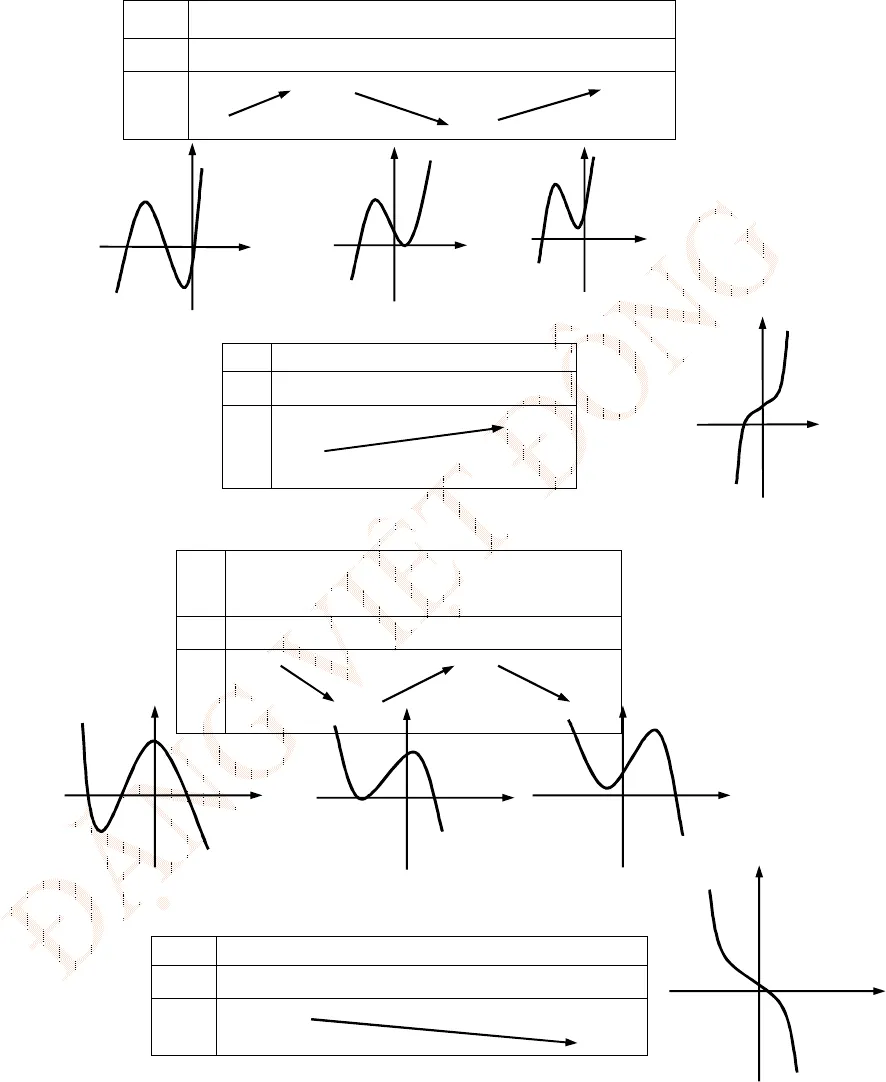    ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Bản biến thiên và Đồ thị hàm số File Word liên hệ: 0978064165 – Email: [email protected] Trang 3Facebook: https://www.facebook.com/dongpay Nếu0athì: lim ; limx xy y    5. Bảng biến thiên và đồ thị: Trường hợp0a:*23 0b ac   : Hàm số có 2 cực trị *23 0 0,b ac y x        : Hàm số luôn tăng trên .x’yyTrường hợp0a:*23 0b ac   : Hàm số có 2 cực trị.x1x2x’y 0 0y CĐ CT *23 0 0,b ac y x        : Hàm số luôn giảm trên.x’yyMột số tính chất của hàm số bậc ba1. Hàm số có cực đại và cực tiểu khi và chỉ khi: 23 0b ac   .2. Hàm số luôn đồng biến trên 203 0ab ac    3. Hàm số luôn nghịch biến trên203 0ab ac    4. Để tìm giá cực trị ta lấy ( )f xchia cho( )f x: ( ) ( ). ( )f x f x g x rx q  x1x2x’y 00yCĐ  CT