Download.vn Học tập Lớp 12
Bạn đang đọc: Chuyên đề cô lập đường thẳng trong biện luận đồ thị hàm số có chứa tham số
Chuyên đề cô lập đường thẳng trong biện luận đồ thị hàm số có chứa tham số Tài liệu ôn tập môn Toán lớp 12
Giới thiệu Tải về Bình luận
- 1
Mua tài khoản Download Pro để trải nghiệm website Download.vn KHÔNG quảng cáo & tải File cực nhanh chỉ từ 79.000đ. Tìm hiểu thêm Mua ngay
Chuyên đề cô lập đường thẳng trong biện luận đồ thị hàm số có chứa tham số là tài liệu hữu ích mà hôm nay Download.vn muốn giới thiệu đến quý thầy cô cùng các bạn học sinh lớp 12 tham khảo.
Tài liệu bao gồm 20 trang, hướng dẫn phương pháp cô lập đường thẳng trong biện luận đồ thị hàm số có chứa tham số giúp các bạn học sinh lớp 12 học tốt chương 1 giải tích 12 và có thêm nhiều tài liệu ôn thi THPT Quốc gia môn Toán. Nội dung chi tiết, mời các bạn cùng tham khảo và tải tài liệu tại đây.
Chuyên đề cô lập đường thẳng trong biện luận đồ thị hàm số có chứa tham số
Group: HỎI ĐÁP TOÁN HỌC – Page: Toán dành cho nhóm 9+ và giáo viên __________________________________________________________________________________________________________________________________https://www.facebook.com/groups/traloinhanhmontoan/ CHUYÊN ĐỀ CÔ LẬP ĐƯỜNG THẲNGTRONG BIỆN LUẬN ĐỒ THỊ HÀM SỐ CÓ CHỨA THAM SỐ A. Cơ sở lý thuyết chung I. Các phép biến đổi đồ thị hàm số 1. Phép tịnh tiến theo véc tơ ( )u = a;bBài toán: Cho đồ thị ( )Ccủa hàm số()y f x=tìm đồ thị ( )’Ccủa hàm số()y F x=thu được khitịnh tiến ( )Ctheo véc tơ ( );u a b=.Cách vẽ: – Mỗi điểm ( )00;A x ythuộc đồ thị( )y f x=cho ta một điểm 00′( ‘ ; ‘ )A x ythuộc đồ thị( )y F x=. Khi đó: 0 0 0 00 0 0 0””x x a x x aAA uy y b y y b− = = −= − = = −- Điểm ( )( )00′ ‘ ; ‘ ‘A x y Cnên00′ ( ‘ )y F x=– Điểm ( )( )00;A x y Cnên( ) ( )0 0 0 0”y f x y b f x a= − = −Do đó: ( )( )( )( ) ( )( )0 0 0 00 0 0 000′ ‘ ‘ ” ‘ ‘ ”’y F x y F xy b f x a F x b f x ay f x a b==− = − − = − = − +Vậy sau phép tịnh tiến ta thu được đồ thị( )’Clà( )y f x a b= − +Bài toán nghịch: Vẽ đồ thị hàm số ()y f x m n= + +từ đồ thị()y f x=Cách vẽ: Đồng nhất ( ) ( )( )y F x f x a by f x m n= = − += + +ta có:( );amu m nbn=− = −=Ghi nhớ: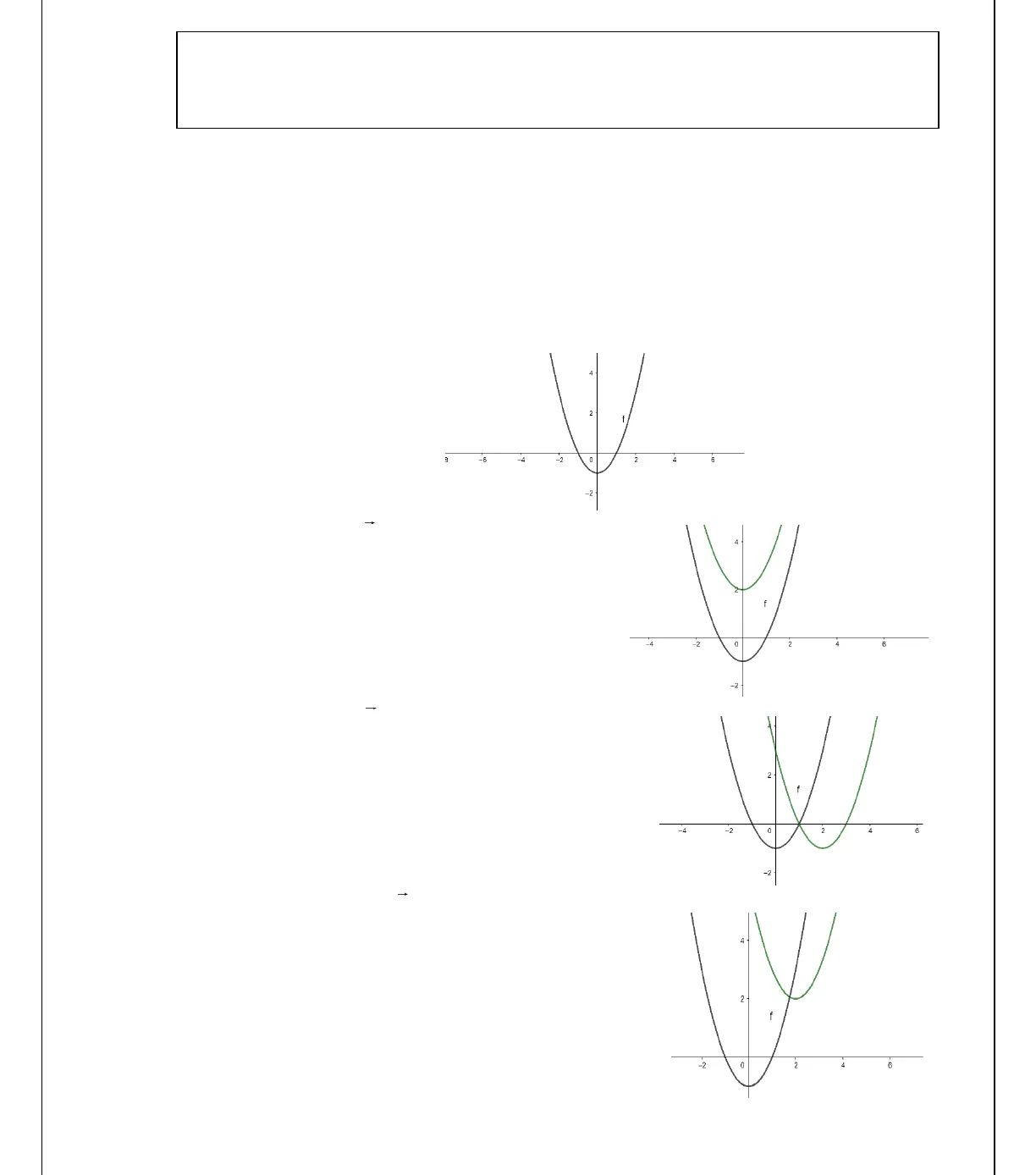 
Group: HỎI ĐÁP TOÁN HỌC – Page: Toán dành cho nhóm 9+ và giáo viên __________________________________________________________________________________________________________________________________https://www.facebook.com/groups/traloinhanhmontoan/ Áp dụng:Ví dụ 1: Cho hàm số 2( ) 1y f x x= = −, vẽ đồ thị các hàm số a) ( ) 3y f x=+b) ( 2)y f x=−c) ( 2) 3y f x= − +Giải: 2( ) 1y f x x= = −a) ( ) 3 ( ; ) (0;3)y f x u m n= + = − =ta dịchchuyển lên trên 3 đơn vị b) ( 2) ( ; ) (2;0)y f x u m n= − = − =ta dịchchuyển sang phải 2 đơn vị c) ( 2) 3 ( ; ) (2;3)y f x u m n= − + = − =ta dịchchuyển sang phải 2 đơn vị và lên trên 3 đơn vị Để thu được ( )( )’:C y f x m n= + +từ( ) ( ):C y f x=ta dịch chuyển đồ thị ( )Csang tráimđơn vị và lên trênnđơn vị.
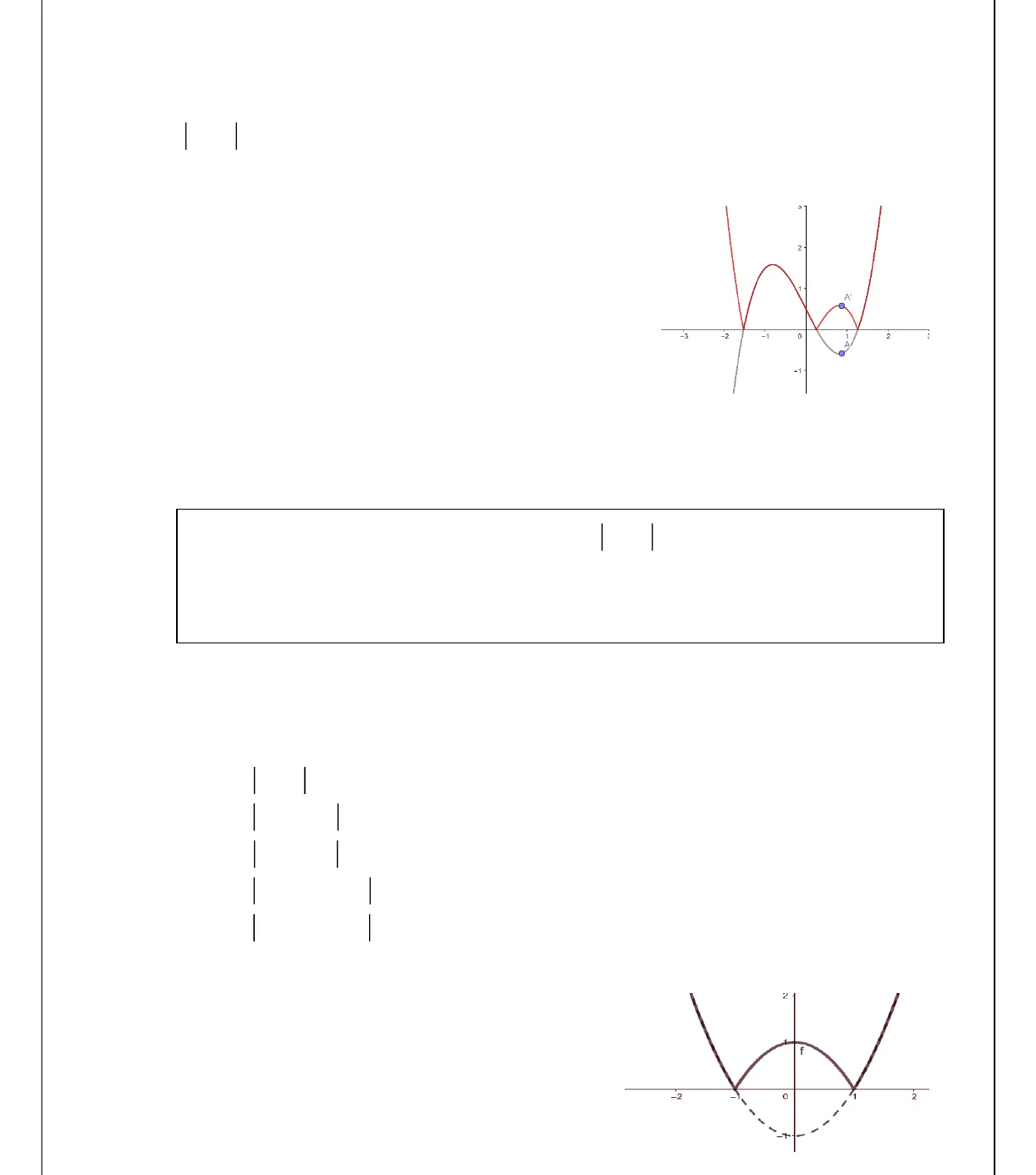Group: HỎI ĐÁP TOÁN HỌC – Page: Toán dành cho nhóm 9+ và giáo viên __________________________________________________________________________________________________________________________________https://www.facebook.com/groups/traloinhanhmontoan/ 2. Phép đối xứng qua trục OxBài toán: Cho đồ thị ( )Ccủa hàm số()y f x=, vẽ đồ thị ( )’Ccủa hàm số()y f x=.Cách vẽ: Tại những điểm ( )00;A x ytrên( )Cqua phép đối xứng qua trục Oxchođiểm ( )00′;A x y−thuộc độ thị ( )’C. Ta luôn có:0 0 00 0 0′ , 0′ , 0y y yy y y= = − Do đó ta có đồ thị ( )’Cbao gồm phần đồ thị ( )Ccó tung độ không âm và tập hợp những điểm đối xứng với ( )Ckhi( )Ccó tung độ âm.Ghi nhớ:Áp dụng Ví dụ 2: Cho hàm số 2( ) 1y f x x= = −, vẽ đồ thị các hàm số a) ()y f x=b) ( 2)y f x=−c) ( ) 3y f x=−d) ( 2) 3y f x= − −e) 4( 2) 3y f x= − − +Giải: a) Vẽ đồ thị hàm số ()y f x=rồi lấy đối xứng phần bên dưới trục OxĐể thu được đồ thị ( )’Ccủa hàm số()y f x=từ đồ thị( )Ccủa hàm số()y f x=, ta giữ nguyên phần đồ thị( )Cở nửa trên trục Oxvà lấy đối xứngvới đồ thị( )Cở nửa dưới trục Ox.