Download.vn Học tập Lớp 11 Toán 11
Bạn đang đọc: Chuyên đề đạo hàm và ý nghĩa của đạo hàm
Chuyên đề đạo hàm và ý nghĩa của đạo hàm Tài liệu ôn tập môn Toán lớp 11
Giới thiệu Tải về Bình luận
- 2
Mua tài khoản Download Pro để trải nghiệm website Download.vn KHÔNG quảng cáo & tải File cực nhanh chỉ từ 79.000đ. Tìm hiểu thêm Mua ngay
Chuyên đề đạo hàm và ý nghĩa của đạo hàm là tài liệu vô cùng hữu ích mà Download.vn muốn giới thiệu đến các bạn học sinh lớp 11, 12 cùng tham khảo.
Chủ đề đạo hàm là phần kiến thức cơ bản và là nên tảng đề các bạn học sinh tìm hiểu sâu hơn về ý nghĩa của đạo hàm nói chung và phương trình tiếp tuyến của hàm số nói riêng. Từ năm tuyển sinh 2018, bộ GD&ĐT đã đưa thêm phần kiến thức của khối lớp 11 vào cấu trúc đề thi, do đó các bạn học sinh cần chuẩn bị những kiến thức căn bản để có thể sử dụng một cách nhanh gọn các đề thi trắc nghiệm. Nội dung chi tiết tài liệu mời các bạn cùng tham khảo và tải tại đây.
Chuyên đề đạo hàm và ý nghĩa của đạo hàm
MỤC LỤCChương 1 ÔN TẬP: Đạo hàm và ứng dụng 21.1 Các công thức cần nhớ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 21.2 Ý nghĩa hình học của đạo hàm . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 41.2.1 Ý nghĩa hình học của đạo hàm . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 41.2.2 Viết phương tr ình tiếp tuyến tại điểm giao với trục Ox,Oy hoặc giao với đồ thị hàmsố khác . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 71.2.3 Viết phương trình tiếp tuyến biết hệ số góc . . . . . . . . . . . . . . . . . . . . . . 81.2.4 Viết phương trình tiếp tuyến qua điểm cho trước . . . . . . . . . . . . . . . . . . . . 111.2.5 Các bài toán tiếp tuyến chứa tham số m . . . . . . . . . . . . . . . . . . . . . . . . 121.3 Ý nghĩa vật lý của đạo hàm . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 121.3.1 Ý nghĩa vật lý của đạo hàm . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 121.4 Các bài toán liên quan đến đạo hàm . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 151.4.1 Các bài toán liên quan đến đạo hàm . . . . . . . . . . . . . . . . . . . . . . . . . . 151.5 Đáp án . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 191.6 Lời giải chi tiết . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 201
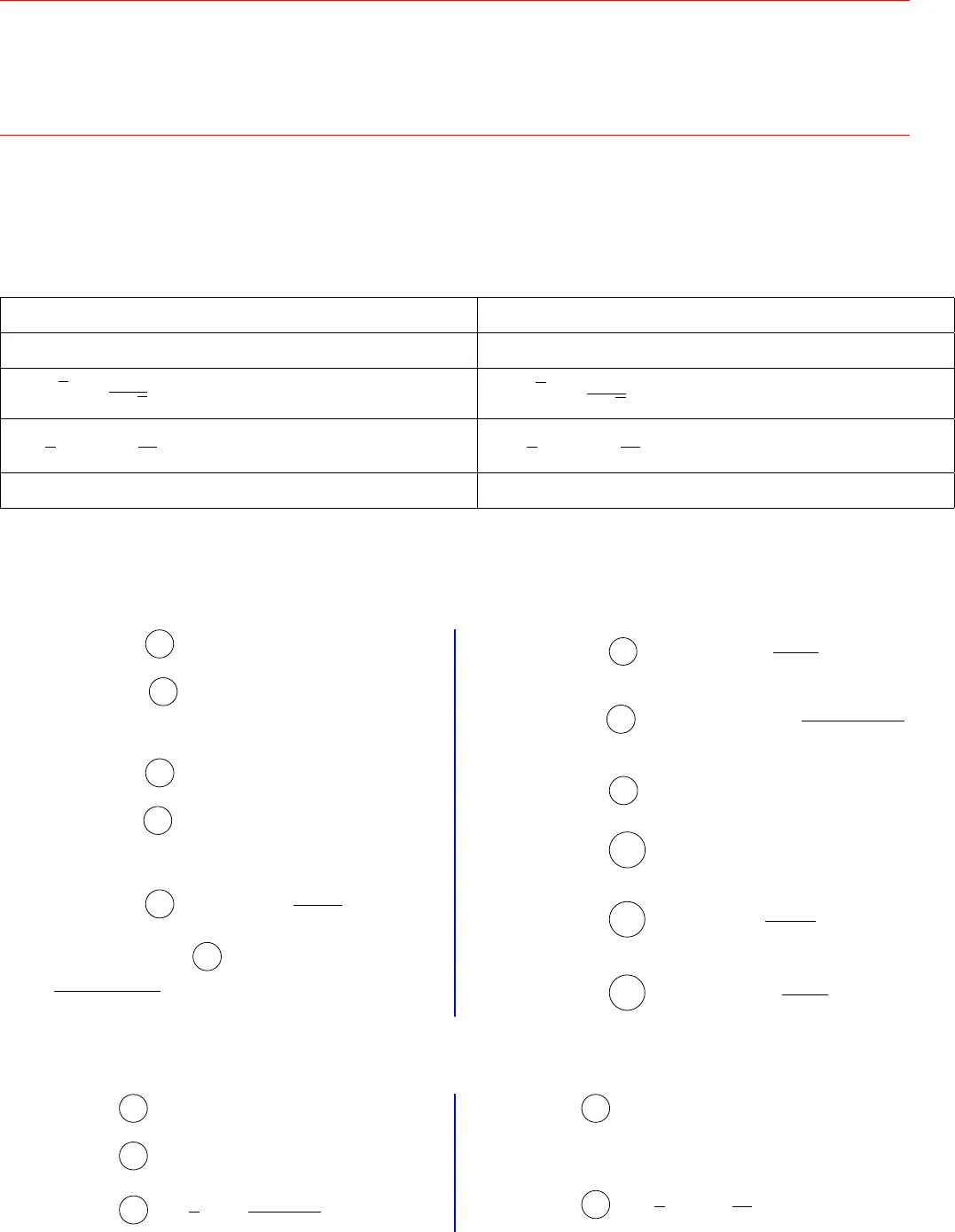CHƯƠNG 1ÔN TẬP: ĐẠO HÀM VÀ ỨNG DỤNG§1.1 Các công thức cần nhớ1. c0= 0 2. x0= 13.xn0= n.xn−1(n ∈ N,n > 1) 4.un0= n.un−1.u0(n ∈ N,n > 1)5. (√x)0=12√x6. (√u)0=u02√u7.1x0= −1×28.1u0= −u0u29. (kx)0= k 10. (ku)0= k.u0Bảng 1.1: Bảng đạo hàm các hàm cơ bảnĐạo hàm của hàm lượng giác1. Công thức 1 . (sin x)0= cos x.2. Công thức 2 . (sin(ax + b))0= a cos(ax +b).3. Công thức 3 . (cos x )0= −sin x.4. Công thức 4 . (cos(ax+b))0= −a sin(ax +b).5. Công thức 5 . (tan x )0=1cos2x.6. Công thức 6 . (tan(ax + b))0=acos2(ax + b).7. Công thức 7 . (cot x)0= −1sin2x.8. Công thức 8 . (cot(ax+b))0= −asin2(ax + b).9. Công thức 9 . (sin u)0= u0.cos u.10. Công thức 10 . (cos u)0= −u0.sin u.11. Công thức 11 . (tan u)0=u0cos2u.12. Công thức 12 . (cot u)0= −u0sin2u.Các quy tắc tính đạo hàm1. Qui tắc 1 . (u ±v)0= u0±v0.2. Qui tắc 2 . (uv)0= u0v + uv0.3. Qui tắc3 .uv0=u0v −uv0v2.4. Hệ quả 1 . (ku)0= ku0.5. Hệ quả 2 .1u0= −u0u2.Các định lý nghiệm tam thức f (x) = ax2+ bx + c2
CHƯƠNG 1. ÔN TẬP: ĐẠO HÀM VÀ ỨNG DỤNG Thầy Lê Minh Cường – 016666582311. f (x) = 0 có 2 nghiệm phân biệt ⇔a 6= 0∆ > 0.2. f (x) = 0 có nghiệm kép ⇔a 6= 0∆ = 0.3. f (x) = 0 có 2 nghiệm trái dấu ⇔ ac 0.4. f (x) = 0 có 2 nghiệm dương pb ⇔a 6= 0∆ > 0S > 0P > 0.5. f (x) = 0 có 2 nghiệm âm pb ⇔a 6= 0∆ > 0S 0P > 0.6. f (x) ≤ 0, ∀x ∈ R ⇔a 0∆ ≤ 0.7. f (x) ≥ 0, ∀x ∈ R ⇔a > 0∆ ≤ 0.Định lý Vi-ét: Nếu x1,x2là 2 nghiệm phân biệt của ax2+ bx + c = 0 thìx1+ x2=−bax1.x2=ca.? Luyện thi 10 – 11 – 12 – THPT QG tại Sài Gòn ? Page 3 of 23