Download.vn Học tập Lớp 12
Bạn đang đọc: Chuyên đề giới hạn của dãy số
Chuyên đề giới hạn của dãy số Tài liệu ôn tập môn Toán lớp 11
Giới thiệu Tải về Bình luận
- 1
Mua tài khoản Download Pro để trải nghiệm website Download.vn KHÔNG quảng cáo & tải File cực nhanh chỉ từ 79.000đ. Tìm hiểu thêm Mua ngay
Với mong muốn đến cho các bạn lớp 11, 12 có thêm tài liệu môn Toán Download.vn xin giới thiệu Chuyên đề giới hạn của dãy số.
Đây là tài liệu rất hữu ích, gồm 30 trang trình bày lý thuyết, phương pháp giải và bài tập trắc nghiệm chuyên đề giới hạn của dãy số với 2 dạng toán thường gặp. Hi vọng với tài liệu này các bạn có thêm nhiều tài liệu học tập, củng cố kiến thức để đạt được kết quả cao trong các bài kiểm tra, bài thi THPT Quốc gia. Mời các bạn cùng theo dõi bài viết dưới đây.
Chuyên đề giới hạn của dãy số
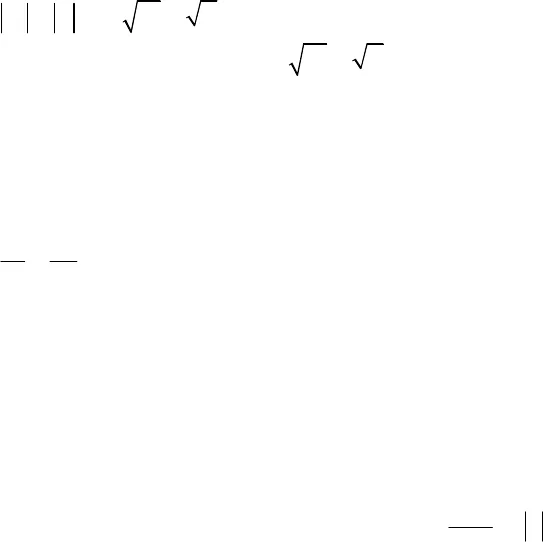 Chuyên đề: Giới hạn dãy số– Chương IV: Đại số và Giải tích 11Nguyễn Quốc Tuấn (Tổng biên tập của Xuctu.com)-090.567.1232 Trang số 1 CHƯƠNG IV: GIỚI HẠNCHỦ ĐỀ 1 : GIỚI HẠN CỦA DÃY SỐDạng 1: Tìm giới hạn của dãy sốI. Dãy số có giới hạn hữu hạn1. Định nghĩa: Ta nói dãy số (un) có giới hạn là L hay (un) dần tới L khi ndần tới vô cực (n ), nếu lim 0.nnu L Kí hiệu: nlim hay u khi n + .nnu L L Chú ý: lim limn nnu u.2. Một số định lý: Định lí 1: Giả sử limnu L, khi đó: 33lim ,limn nu L u L Nếu 0, 0nu n L vàlimnu L Định lí 2: Giả sử lim ,lim ,n nu L v M c const lim( )n nu v L M lim( )n nu v L M lim( . ) .n nu v L M,lim . .nc u c L lim ( 0)nnuLMv M Định lí 3: Cho 3 dãy số ( ),( ),( )n n nu v w. Nếu,n n nu v w n vàlim lim limn n nu w L v L Định lí 4: Dãy số tăng và bị chặn trên thì có giới hạn. Dãy số giảm và bị chặn dưới thì có giới hạn.3. Tổng của cấp số nhân lùi vô hạn:S = u1+ u1q + u1q2+ … =11uq 1qII. DÃY SỐ CÓ GIỚI HẠN VÔ CỰC1. Dãy số có giới hạn :limnu mọi số hạng của dãy số đềulớn hơn một số dương tùy ý cho trước kể từ số hạng nào đó trở đi. 2. Dãy số có giới hạn :limnu mọi số hạng của dãy số đềunhỏ hơn một số âm tùy ý cho trước kể từ số hạng nào đó trở đi.
Chuyên đề: Giới hạn dãy số– Chương IV: Đại số và Giải tích 11Nguyễn Quốc Tuấn (Tổng biên tập của Xuctu.com)-090.567.1232 Trang số 1 CHƯƠNG IV: GIỚI HẠNCHỦ ĐỀ 1 : GIỚI HẠN CỦA DÃY SỐDạng 1: Tìm giới hạn của dãy sốI. Dãy số có giới hạn hữu hạn1. Định nghĩa: Ta nói dãy số (un) có giới hạn là L hay (un) dần tới L khi ndần tới vô cực (n ), nếu lim 0.nnu L Kí hiệu: nlim hay u khi n + .nnu L L Chú ý: lim limn nnu u.2. Một số định lý: Định lí 1: Giả sử limnu L, khi đó: 33lim ,limn nu L u L Nếu 0, 0nu n L vàlimnu L Định lí 2: Giả sử lim ,lim ,n nu L v M c const lim( )n nu v L M lim( )n nu v L M lim( . ) .n nu v L M,lim . .nc u c L lim ( 0)nnuLMv M Định lí 3: Cho 3 dãy số ( ),( ),( )n n nu v w. Nếu,n n nu v w n vàlim lim limn n nu w L v L Định lí 4: Dãy số tăng và bị chặn trên thì có giới hạn. Dãy số giảm và bị chặn dưới thì có giới hạn.3. Tổng của cấp số nhân lùi vô hạn:S = u1+ u1q + u1q2+ … =11uq 1qII. DÃY SỐ CÓ GIỚI HẠN VÔ CỰC1. Dãy số có giới hạn :limnu mọi số hạng của dãy số đềulớn hơn một số dương tùy ý cho trước kể từ số hạng nào đó trở đi. 2. Dãy số có giới hạn :limnu mọi số hạng của dãy số đềunhỏ hơn một số âm tùy ý cho trước kể từ số hạng nào đó trở đi.  Chuyên đề: Giới hạn dãy số– Chương IV: Đại số và Giải tích 11Nguyễn Quốc Tuấn (Tổng biên tập của Xuctu.com)-090.567.1232 Trang số 2 Chú ý:lim lim( ) n nu u3. Một vài qui tắc tìm giới hạn vô cực: o Qui tắc 1: limnulimnvlim .n nu vo Qui tắc 2: limnuDấu củalimnv Llim .n nu vo Qui tắc 3: lim 0nu L Dấu của Llim 0, 0n nv v Dấu củalimnvlimnnuv+-
Chuyên đề: Giới hạn dãy số– Chương IV: Đại số và Giải tích 11Nguyễn Quốc Tuấn (Tổng biên tập của Xuctu.com)-090.567.1232 Trang số 2 Chú ý:lim lim( ) n nu u3. Một vài qui tắc tìm giới hạn vô cực: o Qui tắc 1: limnulimnvlim .n nu vo Qui tắc 2: limnuDấu củalimnv Llim .n nu vo Qui tắc 3: lim 0nu L Dấu của Llim 0, 0n nv v Dấu củalimnvlimnnuv+- Chuyên đề: Giới hạn dãy số– Chương IV: Đại số và Giải tích 11Nguyễn Quốc Tuấn (Tổng biên tập của Xuctu.com)-090.567.1232 Trang số 3 Loại 1: Giới hạn của dãy số hữu tỉPhương pháp: Xem xét bậc cao nhất của tư và mẫu. Sau đó, chia tử và mẫu cho bậc cao nhất của tử và mẫu. Hoặc cũng có thể đặt nhân tử caonhất của từ và mẫu để được những giới hạn cơ bản. Tính giới hạn này. Hướng dẫn giảia. Ta có biến đổi:33 232 3323 655 3 6lim lim4 74 3 73nn nn nn n nnn n 323 655lim4 733n nn n Vì khin thì323lim 06lim 04lim 07lim 0nnnnb. Ta có biến đổi:4 22 46 2 1lim1 5 3n nn n =44 22 42 444 22 166 2 1lim lim1 51 5 33nn nn nn nnn n 2 44 22 16lim1 53n nn n =-2Bài tập mẫu 1: Tính các giới hạn sau: a.3 22 35 3 6lim4 3 7n nn n n c.222 3lim3 2 1n nn n b.4 22 46 2 1lim1 5 3n nn n d.222 3 1lim1n nn e.24 2017lim4 1nn n f. n nn21 4lim3 2
Chuyên đề: Giới hạn dãy số– Chương IV: Đại số và Giải tích 11Nguyễn Quốc Tuấn (Tổng biên tập của Xuctu.com)-090.567.1232 Trang số 3 Loại 1: Giới hạn của dãy số hữu tỉPhương pháp: Xem xét bậc cao nhất của tư và mẫu. Sau đó, chia tử và mẫu cho bậc cao nhất của tử và mẫu. Hoặc cũng có thể đặt nhân tử caonhất của từ và mẫu để được những giới hạn cơ bản. Tính giới hạn này. Hướng dẫn giảia. Ta có biến đổi:33 232 3323 655 3 6lim lim4 74 3 73nn nn nn n nnn n 323 655lim4 733n nn n Vì khin thì323lim 06lim 04lim 07lim 0nnnnb. Ta có biến đổi:4 22 46 2 1lim1 5 3n nn n =44 22 42 444 22 166 2 1lim lim1 51 5 33nn nn nn nnn n 2 44 22 16lim1 53n nn n =-2Bài tập mẫu 1: Tính các giới hạn sau: a.3 22 35 3 6lim4 3 7n nn n n c.222 3lim3 2 1n nn n b.4 22 46 2 1lim1 5 3n nn n d.222 3 1lim1n nn e.24 2017lim4 1nn n f. n nn21 4lim3 2
