Download.vn Học tập Lớp 12
Bạn đang đọc: Chuyên đề góc và khoảng cách trong không gian
Chuyên đề góc và khoảng cách trong không gian Tài liệu ôn thi THPT Quốc gia 2019
Giới thiệu Tải về Bình luận
- 1
Mua tài khoản Download Pro để trải nghiệm website Download.vn KHÔNG quảng cáo & tải File cực nhanh chỉ từ 79.000đ. Tìm hiểu thêm Mua ngay
Chuyên đề góc và khoảng cách trong không gian là tài liệu cực kì hữu ích mà Download.vn muốn giới thiệu đến các bạn học sinh lớp 12 cùng tham khảo.
Tài liệu bao gồm 66 trang được biên soạn bởi thầy Nguyễn Hữu Nhanh Tiến hướng dẫn phương pháp giải các dạng toán chuyên đề góc và khoảng cách trong không gian. Nội dung chi tiết, mời các bạn cùng tham khảo và tải tài liệu tại đây.
Chuyên đề góc và khoảng cách trong không gian
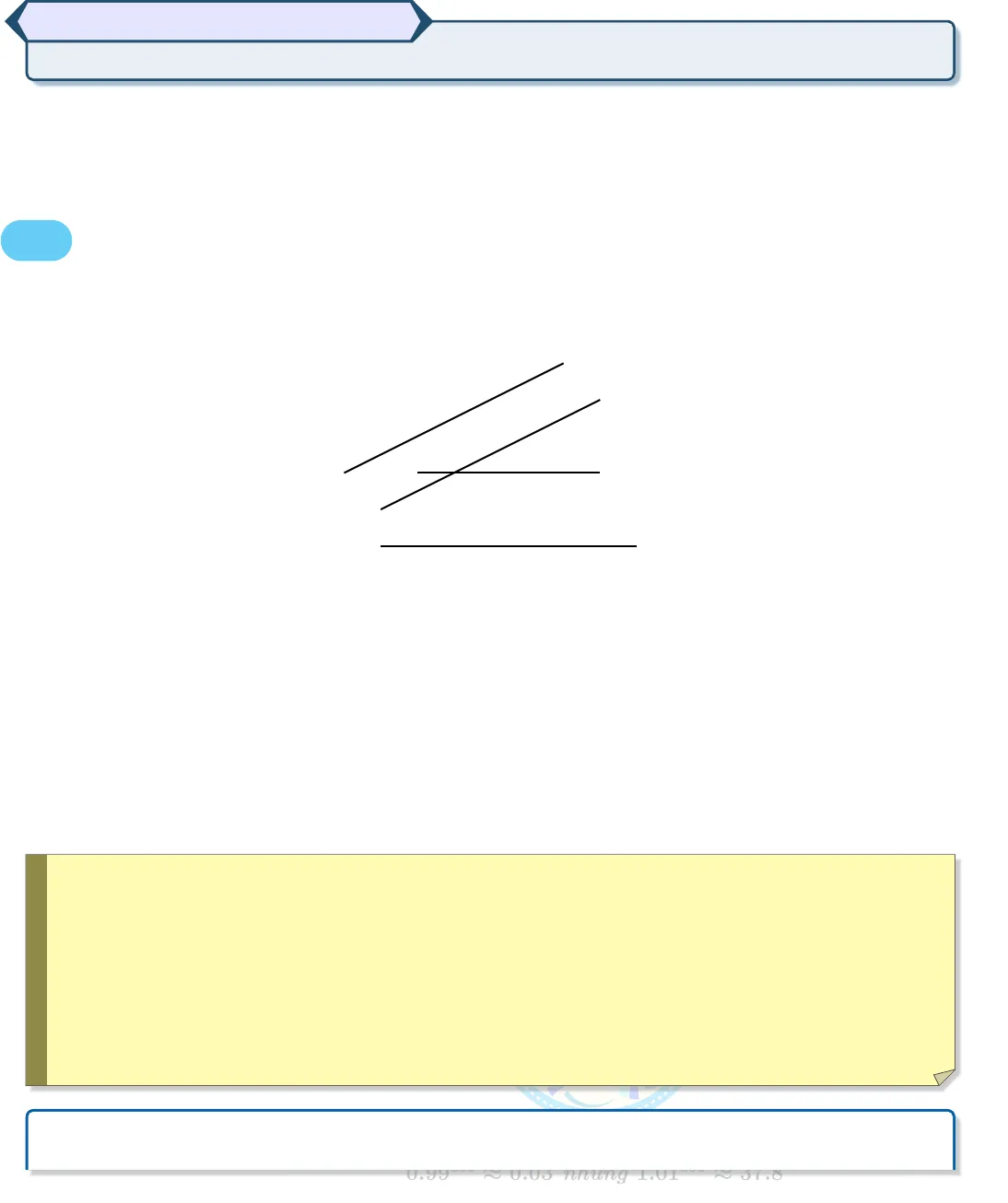Ð LATEX Hóa Nguyễn Hữu Nhanh Tiến h /ToanTienNhanhHướng tới kì thi THPTQG 2019GÓC – KHOẢNG CÁCH§1. Các dạng toán liên quan đến tính Góc1. 1 Góc giữa hai đường thẳngGóc giữa hai đường thẳng a và b trong không gian là góc giữa hai đường thẳng a0và b0cùng đi quamột điểm và lần lượt song song với a và b.aa0bb0OL Để xác định góc giữa hai đường thẳng a và b ta có thể lấy điểm O thuộc một trong hai đườngthẳng đó rồi vẽ một đường thẳng qua O và song song với đường thẳng còn lại.L Nếu#»u và#»v lần lượt là vec-tơ chỉ phương của a và b, đồng thời (#»u ,#»v ) = α thì góc giữa haiđường thẳng a và b bằng α nếu 0◦≤ α ≤ 90◦và bằng 180◦− α nếu 90◦ α ≤ 180◦.L Nếu a và b là hai đường thẳng song song hoặc trùng nhau thì góc giữa chúng bằng 0◦.!Xác định góc giữa hai đường thẳng trong không gian. Ta thường có hai phương pháp để giảiquyết cho dạng toán này.¹ Phương pháp 1: Sử dụng định nghĩa góc giữa hai đường thẳng, kết hợp sử dụng hệ thứclượng trong tam giác (định lý cos, công thức trung tuyến).¹ Phương pháp 2: Sử dụng tích vô hương của hai vec-tơ.Ví dụ 1.161 -Bùi Thị Xuân Tp Huế 1 TT Quốc Học Huế
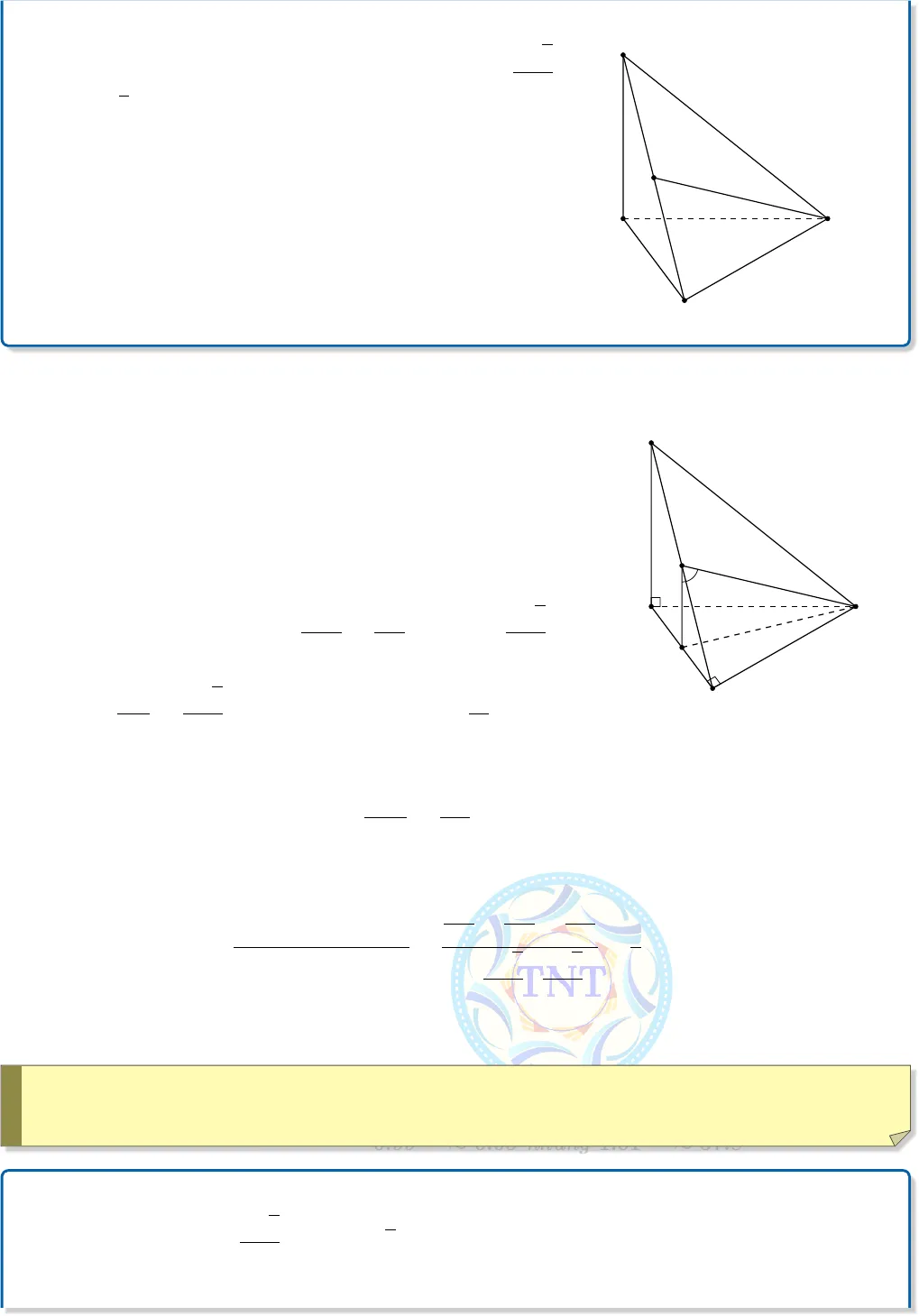Ð LATEX Hóa Nguyễn Hữu Nhanh Tiến h /ToanTienNhanhCho tứ diện ABCD có AB vuông góc với mặt phẳng(BCD). Biết tam giác BCD vuông tại C và AB =a√62,AC = a√2, CD = a. Gọi E là trung điểm của AC (thamkhảo hình vẽ bên). Góc giữa hai đường thẳng AB và DEbằngA. 45◦. B. 60◦. C. 30◦. D. 90◦.B DEAC Hướng dẫn giải:Gọi I là trung điểm của BC, suy ra EI k AB.Khi đó (AB, DE) = (EI, ED) =[IED.Ta cóDC ⊥ BC (giả thiết)DC ⊥ AB (AB ⊥ (BCD))⇒ DC ⊥ (ABC),suy ra DC vuông góc với EC. Do đóDE2= CD2+ EC2= CD2+AC24=3a22⇒ DE =a√62.Ta có IE =AB2=a√64và BC2= AC2− AB2=a22.Tam giác ICD vuông tại C nênDI2= CD2+ IC2= CD2+BC24=9a28.B DEACIÁp dụng định lý cô-sin cho tam giác IDE, ta cócos[IED =IE2+ DE2− CD22IE · DE=3a28+3a22−9a282 ·a√64·a√62=12⇒[IED = 60◦.Vậy góc giữa hai đường thẳng AB và DE bằng 60◦.!Có thể chứng minh EI vuông góc với mặt phẳng (BCD), suy ra tam giác EID vuông tại I đểtính góc[IED đơn giản hơn mà không cần sử dụng định lý cô-sin.Ví dụ 2. Cho tứ diện ABCD có AB vuông góc với mặt phẳng (BCD). Biết tam giác BCDvuông tại C và AB =a√62, AC = a√2, CD = a. Gọi E là trung điểm của AD (tham khảohình vẽ dưới đây).161 -Bùi Thị Xuân Tp Huế 2 TT Quốc Học Huế
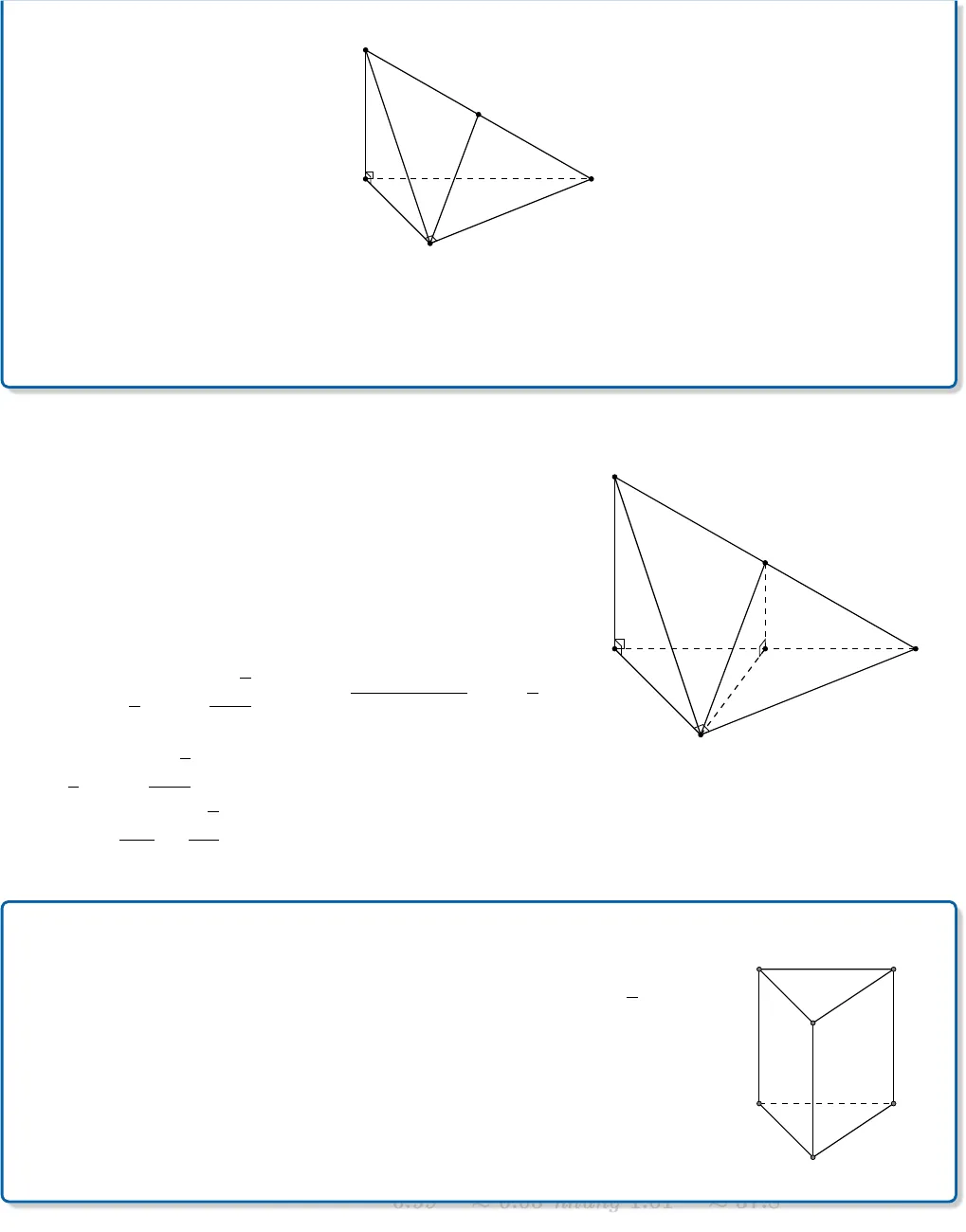Ð LATEX Hóa Nguyễn Hữu Nhanh Tiến h /ToanTienNhanhB DECAGóc giữa hai đường thẳng AB và CE bằngA. 60◦. B. 45◦. C. 30◦. D. 90◦. Hướng dẫn giải:Gọi F là trung điểm của BD, suy ra EF k AB nên(AB, CE) = (EF, CE).Do AB ⊥ (BCD) nên EF ⊥ (BCD), suy ra 4EF Cvuông tại F .Mặt khácCD ⊥ BCCD ⊥ AB⇒ CD ⊥ AC.Ta có EF =12AB =a√64, AD =√AC2+ CD2= a√3.4ACD vuông tại C và có E là trung điểm của AD nênCE =12AD =a√32.cos[CEF =EFEC=√22⇒[CEF = 45◦.Vậy (AB, CE) = (EF, CE) =[CEF = 45◦.B DECFAVí dụ 3.Cho hình lăng trụ đứng tam giác ABC.A0B0C0có đáy ABC là tamgiác cân AB = AC = a,[BAC = 120◦, cạnh bên AA0= a√2. Tínhgóc giữa hai đường thẳng AB0và BC (tham khảo hình vẽ bên).A. 90◦. B. 30◦. C. 45◦. D. 60◦.BCB0C0AA0 Hướng dẫn giải:161 -Bùi Thị Xuân Tp Huế 3 TT Quốc Học Huế