Download.vn Học tập Lớp 12
Bạn đang đọc: Chuyên đề hình học giải tích không gian
Chuyên đề hình học giải tích không gian Tài liệu ôn tập môn Toán lớp 12
Giới thiệu Tải về Bình luận
- 1
Mua tài khoản Download Pro để trải nghiệm website Download.vn KHÔNG quảng cáo & tải File cực nhanh chỉ từ 79.000đ. Tìm hiểu thêm Mua ngay
Mời quý thầy cô giáo cùng các bạn học sinh lớp 12 cùng tham khảo tài liệu Chuyên đề hình học giải tích không gian được Download.vn đăng tải ngay sau đây.
Chuyên đề hình học giải tích không gian là tài liệu cực kì hữu ích, gồm 59 trang tổng hợp toàn bộ phần lý thuyết, công thức, bài tập có đáp án và tuyển tập các bài hình học tọa độ không gian trong đề thi THPT Quốc gia. Hi vọng với tài liệu này các bạn có thêm nhiều tài liệu tham khảo để đạt được nhiều kết quả trong các bài thi học kì và thi THPT Quốc gia sắp tới.
Chuyên đề hình học giải tích không gian
GV.Lưu Huy Thưởng 0968.393.899 BỂ HỌC VÔ BỜ – CHUYÊN CẦN SẼ ĐẾN BẾNCHUYÊN ĐỀHÌNH HỌC GIẢI TÍCH TRONG KHÔNG GIANBÀI 1: MỞ ĐẦUI. VEC TƠ TRONG KHÔNG GIAN1. Định nghĩa và các phép toán • !”#$$#%&’( •)*+, -Qui tắc ba điểm:./0%12./34,AB BC AC+ = -Qui tắc hình bình hành:.5/5$12.64,AB AD AC+ = -Qui tắc hình hộp:.5712.6(1′2′.′6′4,’ ‘AB AD AA AC+ + = -Hê thức trung điểm đoạn thẳng:.89$*0%:;’12 =4, 0IA IB+ = > 2OA OB OI+ = -Hệ thức trọng tâm tam giác:.?9$@ %:%12.+( =4, 0; 3GA GB GC OA OB OC OG+ + = + + = -Hệ thức trọng tâm tứ diện:.?9$@ %:A“B12.6 =4, 0; 4GA GB GC GD OA OB OC OD OG+ + + = + + + = -Điều kiện hai vectơ cùng phương: ( 0) ! :≠ ⇔ ∃ ∈ = a vaø b cuøng phöông a k R b ka -Điểm M chia đoạn thẳng AB theo tỉ số kC≠D =4, ;1OA kOBMA kMB OMk−= =− 2. Sự đồng phẳng của ba vectơ •2@9$E’F*:GHIIJ%7%&’( •Điều kiện để ba vectơ đồng phẳng:./, ,a b c 4a vaø bH(K4,, ,a b c E’⇔∃L%∈M,c ma nb= + •./, ,a b c E’x*3+( K4, ∃L%∈M,x ma nb pc= + + 3. Tích vô hướng của hai vectơ • Góc giữa hai vectơ trong không gian: 0 0, ( , ) (0 180 )AB u AC v u v BAC BAC= = ⇒ = ≤ ≤ 
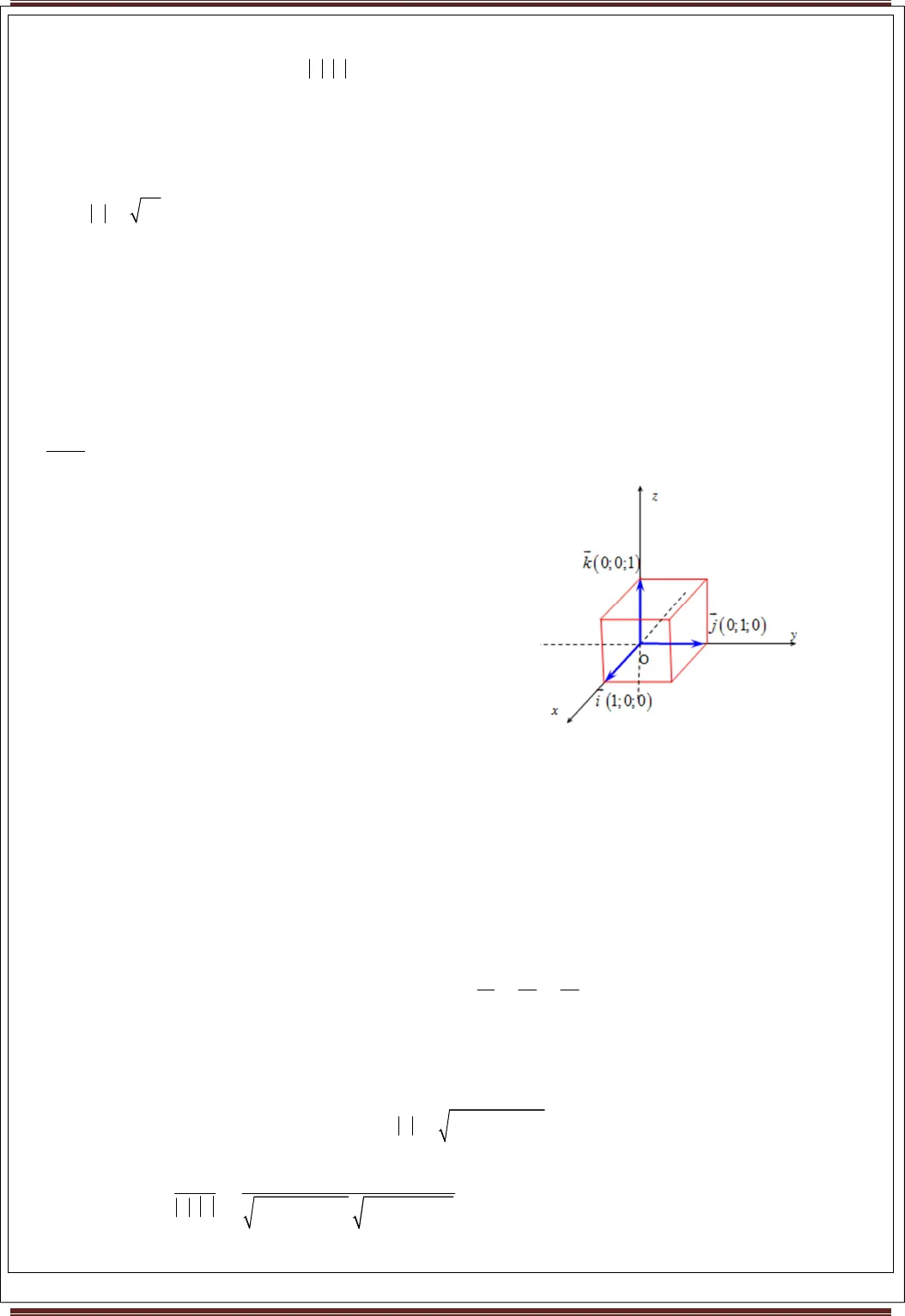GV.Lưu Huy Thưởng 0968.393.899 BỂ HỌC VÔ BỜ – CHUYÊN CẦN SẼ ĐẾN BẾNN •Tích vô hướng của hai vectơ trong không gian: -., 0u v ≠(K4,. . .cos( , )u v u v u v= -OJ 0 0u hoaëc v= = (P*J, . 0u v = - . 0u v u v⊥ ⇔ = -2u u= II. HỆ TỌA ĐỘ TRONG KHÔNG GIAN1. Hệ tọa độ Đêcac vuông góc trong không gian: ./Q
GV.Lưu Huy Thưởng 0968.393.899 BỂ HỌC VÔ BỜ – CHUYÊN CẦN SẼ ĐẾN BẾNY a) Định nghĩa:( ; ; ) ( ; ; )M x y z OM x y z⇔ = (x : hoành độ, y : tung độ, z : cao độ) Chú ý:•M∈(Oxy)⇔z = 0; M∈(Oyz)⇔x = 0; M∈(Oxz)⇔y = 0 ••••M ∈Ox⇔y = z = 0; M∈Oy⇔x = z = 0; M∈Oz⇔x = y = 0 b) Tính chất: .( ; ; ), ( ; ; )A A A B B BA x y z B x y z •( ; ; )B A B A B AAB x x y y z z= − − − •2 2 2( ) ( ) ( )B A B A B AAB x x y y z z= − + − + − •=;70%Z;12[ITk(k≠1): ; ;1 1 1A B A B A Bx kx y ky z kzMk k k − − − − − − •=;7*0%Z:;’12,; ;2 2 2A B A B A Bx x y y z zM + + + •=;7@ %?:%12., ; ;3 3 3A B C A B C A B Cx x x y y y z z zG + + + + + + •=;7@ %?:A”B12.6, ; ;4 4 4A B C D A B C D A B C Cx x x x y y y y z z z zG + + + + + + + + + 4. Tích có hướng của hai vectơ:(Chương trình nâng cao) a) Định nghĩa: Cho1 2 3( , , )a a a a=1 2 3( , , )b b b b=(( )2 3 3 1 1 22 3 3 2 3 1 1 3 1 2 2 12 3 3 1 1 2, ; ; ; ;a a a a a aa b a b a b a b a b a b a b a bb b b b b b = ∧ = = − − − Chú ý: Tích có hướng của hai vectơ là một vectơ, tích vô hướng của hai vectơ là một số. b) Tính chất: •, ; , ; ,i j k j k i k i j = = = •[ , ] ; [ , ]a b a a b b⊥ ⊥ •()[ , ] . .sin ,a b a b a b= •,a b H[ , ] 0a b⇔ = c) Ứng dụng của tích có hướng: •Điều kiện đồng phẳng của ba vectơ: ,a b $cE’⇔[ , ]. 0a b c= •Diện tích hình bình hành ABCD: ,ABCDS AB AD = ▱ •Diện tích tam giác ABC: 1,2ABCS AB AC∆ = •Thể tích khối hộp ABCD.A′′′′B′′′′C′′′′D′′′′: . ‘ ‘ ‘ ‘[ , ]. ‘ABCD A B C DV AB AD AA= 