Download.vn Học tập Lớp 10

Bạn đang đọc: Chuyên đề Hình học giải tích trong mặt phẳng

Chuyên đề Hình học giải tích trong mặt phẳng Tài liệu ôn tập môn Toán lớp 10

Giới thiệu Tải về Bình luận

• 1

Mua tài khoản Download Pro để trải nghiệm website Download.vn KHÔNG quảng cáo & tải File cực nhanh chỉ từ 79.000đ. Tìm hiểu thêm Mua ngay

Chuyên đề Hình học giải tích trong mặt phẳng là tài liệu vô cùng hữu ích mà Downoad.com.vn muốn giới thiệu đến quý thầy cô giáo cùng các em học sinh lớp 10, 11, và lớp 12 cùng theo dõi.

Tài liệu bao gồm 41 trang trình bày lý thuyết phần đường thẳng, đường tròn, Parabol; các bài tập liên quan đến đường thẳng và bài tập có nội dung thuộc Hình học giải tích trong mặt phẳng, kèm đáp án chi tiết giúp các em dễ dàng học tập và ôn tập, chuẩn bị cho kì thi sắp tới. Sau đây là nội dung chi tiết mời các bạn cùng theo dõi và tải tài liệu tại đây.

Chuyên đề Hình học giải tích trong mặt phẳng

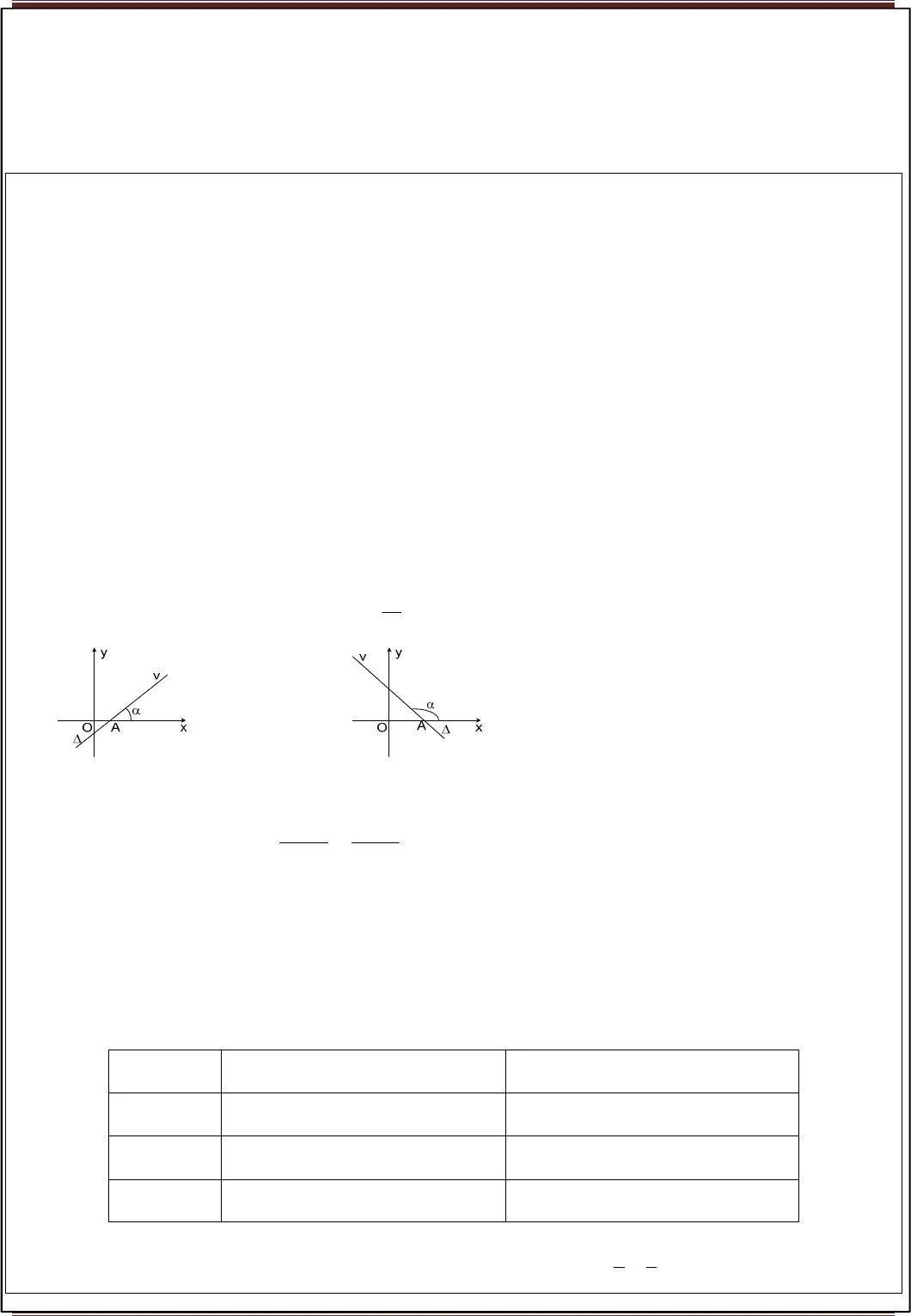GV.Lưu Huy Thưởng 0968.393.899 BỂ HỌC VÔ BỜ – CHUYÊN CẦN SẼ TỚI BẾN Page 1 CHUYÊN ĐỀHÌNH HỌC GIẢI TÍCH TRONG MẶT PHẲNG§1: PHƯƠNG TRÌNH ĐƯỜNG THẲNG1. Vectơ chỉ phương của đường thẳng Vectơ0u≠được gọi là vectơ chỉ phương của đường thẳng ∆ nếu giá của nó song song hoặc trùng với ∆. Nhận xét: – Nếu ulà một VTCP của∆thìku(k≠0) cũng là một VTCP của∆. – Một đường thẳng hoàn toàn được xác định nếu biết một điểm và một VTCP.2. Vectơ pháp tuyến của đường thẳng Vectơ0n≠được gọi là vectơ pháp tuyến của đường thẳng ∆ nếu giá của nó vuông góc với ∆. Nhận xét: – Nếu nlà một VTPT của∆thìkn(k≠0) cũng là một VTPT của∆. – Một đường thẳng hoàn toàn được xác định nếu biết một điểm và một VTPT. – Nếuulà một VTCP vànlà một VTPT của∆thìu n⊥ . 3. Phương trình tham số của đường thẳng Cho đường thẳng ∆ đi qua0 0 0( ; )M x yvà có VTCP1 2( ; )u u u=. Phương trình tham số của ∆:0 10 2= += +x x tuy y tu(1) ( t là tham số). Nhận xét: – M(x; y) ∈∆⇔∃t∈R:0 10 2= += +x x tuy y tu. – Gọi k là hệ số góc của ∆thì: + k = tanα, vớiα=xAv,α≠090. + k =21uu, với10u≠. 4. Phương trình chính tắc của đường thẳng Cho đường thẳng ∆ đi qua0 0 0( ; )M x yvà có VTCP1 2( ; )u u u=. Phương trình chính tắc của ∆:0 01 2x x y yu u− −=(2) (u1≠0, u2≠0). Chú ý: Trong trường hợp u1= 0 hoặc u2= 0 thì đường thẳng không có phương trình chính tắc. 5. Phương trình tham số của đường thẳng PT0ax by c+ + =với2 20a b+ ≠được gọi là phương trình tổng quát của đường thẳng. Nhận xét: – Nếu ∆có phương trình0ax by c+ + =thì∆có: VTPT là ( ; )n a b=và VTCP( ; )u b a= −hoặc( ; )u b a= −. – Nếu∆đi qua0 0 0( ; )M x yvà có VTPT( ; )n a b=thì phương trình của∆là:0 0( ) ( ) 0a x x b y y− + − = Các trường hợp đặc biệt: •∆đi qua hai điểm A(a; 0), B(0; b) (a, b≠0): Phương trình của∆:1x ya b+ =.Các hệ sốPhương trình đường thẳng ∆∆∆∆ Tính chất đường thẳng ∆∆∆∆ c = 00ax by+ =∆đi qua gốc toạ độ Oa = 00by c+ =∆// Ox hoặc∆≡Oxb = 00ax c+ =∆// Oy hoặc∆≡Oy GV.Lưu Huy Thưởng 0968.393.899 BỂ HỌC VÔ BỜ – CHUYÊN CẦN SẼ TỚI BẾN Page 2 (phương trình đường thẳng theo đoạn chắn) . •∆đi qua điểm0 0 0( ; )M x yvà có hệ số góc k: Phương trình của∆:0 0( )y y k x x− = − (phương trình đường thẳng theo hệ số góc)6. Vị trí tương đối của hai đường thẳng Cho hai đường thẳng ∆1:1 1 10a x b y c+ + =và ∆2:2 2 20a x b y c+ + =. Toạ độ giao điểm của ∆1và ∆2là nghiệm của hệ phương trình:1 1 12 2 200a x b y ca x b y c+ + =+ + =(1) • ∆1cắt ∆2⇔ hệ (1) có một nghiệm ⇔1 12 2a ba b≠(nếu 2 2 2, , 0a b c≠) • ∆1// ∆2⇔ hệ (1) vô nghiệm⇔1 1 12 2 2a b ca b c= ≠(nếu 2 2 2, , 0a b c≠) • ∆1≡ ∆2⇔ hệ (1) có vô số nghiệm⇔1 1 12 2 2a b ca b c= =(nếu 2 2 2, , 0a b c≠)7. Góc giữa hai đường thẳng Cho hai đường thẳng ∆1:1 1 10a x b y c+ + =(có VTPT1 1 1( ; )n a b=) và ∆2:2 2 20a x b y c+ + =(có VTPT2 2 2( ; )n a b=).01 2 1 21 20 01 2 1 2( , ) ( , ) 90( , )180 ( , ) ( , ) 90n n khi n nn n khi n n≤∆ ∆ =− >      1 2 1 2 1 21 2 1 22 2 2 21 21 1 2 2.cos( , ) cos( , )..n n a a b bn nn na b a b+∆ ∆ = = =+ +    Chú ý: •∆1⊥∆2⇔1 2 1 20a a b b+ =. •Cho∆1:1 1y k x m= +,∆2:2 2y k x m= +thì: +∆1//∆2⇔k1= k2 +∆1⊥∆2⇔k1. k2= –1. 8. Khoảng cách từ một điểm đến một đường thẳng •Khoảng cách từ một điểm đến một đường thẳng Cho đường thẳng ∆:0ax by c+ + =và điểm0 0 0( ; )M x y. 0 002 2( , )ax by cd Ma b+ +∆ =+•Vị trí tương đối của hai điểm đối với một đường thẳng Cho đường thẳng ∆:0ax by c+ + =và hai điểm( ; ), ( ; )M M N NM x y N x y∉ ∆. – M, N nằm cùng phía đối với ∆ ⇔( )( ) 0M M N Nax by c ax by c+ + + + >. – M, N nằm khác phía đối với ∆ ⇔( )( ) 0M M N Nax by c ax by c+ + + + <.>Phương trình các đường phân giác của các góc tạo bởi hai đường thẳng Cho hai đường thẳng ∆1:1 1 10a x b y c+ + =và ∆2:2 2 20a x b y c+ + =cắt nhau. Phương trình các đường phân giác của các góc tạo bởi hai đường thẳng ∆1và ∆2là: 1 1 1 2 2 22 2 2 21 1 2 2a x b y c a x b y ca b a b+ + + += ±+ + GV.Lưu Huy Thưởng 0968.393.899 BỂ HỌC VÔ BỜ – CHUYÊN CẦN SẼ TỚI BẾN Page 3 VẤN ĐỀ 1: Lập phương trình đường thẳng • Để lập phương trình tham số và phương trình chính tắc của đường thẳng ∆ta cần xác định một điểm0 0 0( ; )M x y∈∆và một VTCP1 2( ; )u u u=của∆. PTTS của∆:0 10 2x x tuy y tu= += +; PTCT của ∆:0 01 2x x y yu u− −=(u1≠0, u2≠0). • Để lập phương trình tổng quát của đường thẳng ∆ ta cần xác định một điểm0 0 0( ; )M x y∈∆và một VTPT( ; )n a b=của∆. PTTQ của∆:0 0( ) ( ) 0a x x b y y− + − = • Một số bài toán thường gặp: +∆đi qua hai điểm( ; ) , ( ; )A A B BA x y B x y(với ,A B A Bx x y y≠ ≠): PT của∆:A AB A B Ax x y yx x y y− −=− − +∆đi qua hai điểm A(a; 0), B(0; b) (a, b≠0): PT của∆:1x ya b+ =. +∆đi qua điểm0 0 0( ; )M x yvà có hệ số góc k: PT của∆:0 0( )y y k x x− = − Chú ý: Ta có thể chuyển đổi giữa các phương trình tham số, chính tắc, tổng quát của một đường thẳng.•Để tìm điểm M′đối xứng với điểm M qua đường thẳng d, ta có thể thực hiện như sau: Cách 1: – Viết phương trình đường thẳng∆qua M và vuông góc với d. – Xác định I = d∩∆(I là hình chiếu của M trên d). – Xác định M′sao cho I là trung điểm của MM′. Cách 2: Gọi I là trung điểm của MM′. Khi đó: M′đối xứng của M qua d⇔dMM uI d′⊥∈(sử dụng toạ độ)•Để viết phương trình đường thẳng d′đối xứng với đường thẳng d qua đường thẳng∆, ta có thể thực hiện như sau: – Nếu d //∆: + Lấy A∈d. Xác định A′đối xứng với A qua∆. + Viết phương trình đường thẳng d′qua A′và song song với d. – Nếu d∩∆= I: + Lấy A∈d (A≠I). Xác định A′đối xứng với A qua∆. + Viết phương trình đường thẳng d′qua A′và I.•Để viết phương trình đường thẳng d′đối xứng với đường thẳng d qua điểm I,∆, ta có thể thực hiện như sau: – Lấy A∈d. Xác định A′đối xứng với A qua I. – Viết phương trình đường thẳng d′qua A′và song song với d.