Download.vn Học tập Lớp 12
Bạn đang đọc: Chuyên đề khảo sát hàm số
Chuyên đề khảo sát hàm số Tài liệu ôn tập môn Toán lớp 12
Giới thiệu Tải về Bình luận
- 4
Mua tài khoản Download Pro để trải nghiệm website Download.vn KHÔNG quảng cáo & tải File cực nhanh chỉ từ 79.000đ. Tìm hiểu thêm Mua ngay
Chuyên đề khảo sát hàm số là tài liệu vô cùng hữu ích mà Download.vn muốn giới thiệu đến quý thầy cô giáo cùng các bạn học sinh lớp 12 cùng tham khảo.
Tài liệu gồm 177 trang hướng dẫn giải các dạng toán chuyên đề khảo sát hàm số, tài liệu do thầy Nguyễn Phú Khánh biên soạn. Nội dung tài liệu gồm 8 bài:
- Tính đơn điệu của hàm số;
- Cực trị hàm số;
- Tiệm cận của hàm số;
- Giá trị lớn nhất và nhỏ nhất của hàm số;
- Phép tịnh tiến và tâm đối xứng;
- Khảo sát sự biến thiên và vẽ đồ thị của hàm số;
- Giao điểm của hai đồ thị.
- Sự tiếp xúc của hai đường cong
Chuyên đề khảo sát hàm số
ŀNguyễn Phú Khánh – Đà Lạt Tài Liệu ôn thi Tú Tài Đại học theo cấu trúc BGD.5Chương 1ỨNG DỤNG CỦA ĐẠO HÀM ĐỂ KHẢO SÁTVÀ VẼ ĐỒ THỊ CỦA HÀM SỐBài 1: TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ1.1 TÓM TẮT LÝ THUYẾT1. Định nghĩa :Giả sửKlà một khoảng , một đoạn hoặc một nửa khoảng . Hàm sốfxác địnhtrênKđược gọi là•Đồng biến trênKnếu với mọi()()1 2 1 2 1 2, ,x x K x x f x f x∈ ⇒ ; •Nghịch biến trênKnếu với mọi()()1 2 1 2 1 2, ,x x K x x f x f x∈ ⇒ > . 2. Điều kiện cần để hàm số đơn điệu :Giả sử hàm sốfcó đạo hàm trên khoảngI•Nếu hàm sốfđồng biến trên khoảngIthì()’ 0f x≥với mọix I∈;•Nếu hàm sốfnghịch biến trên khoảngIthì()’ 0f x≤với mọix I∈.3. Điều kiện đủ để hàm số đơn điệu :Giả sửIlà một khoảng hoặc nửa khoảng hoặc một đoạn ,flà hàm số liên tụctrênIvà có đạo hàm tại mọi điểm trong củaI( tức là điểm thuộcInhưngkhông phải đầu mút củaI) .Khi đó : •Nếu()’ 0f x>với mọix I∈thì hàm sốfđồng biến trên khoảngI;•Nếu()’ 0f x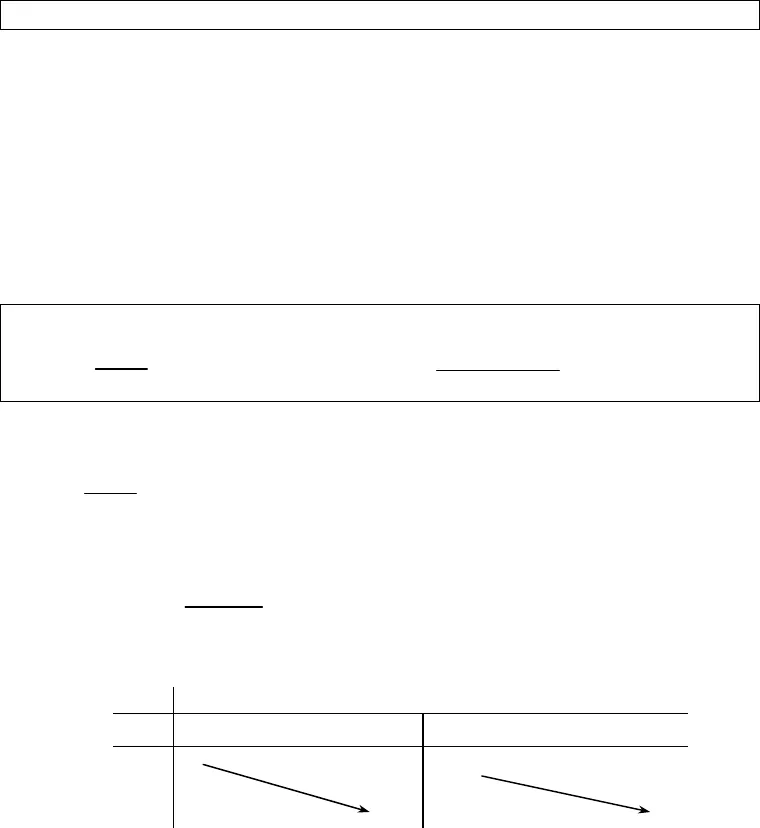
Nguyễn Phú Khánh – Đà Lạt Tài Liệu ôn thi Tú Tài Đại học theo cấu trúc BGD.6*Nếu hàm sốfnghịch biến trên khoảng();a bthì nó nghịch biến trên đoạn;a b .*Nếu hàm sốfkhông đổi trên khoảng();a bthì không đổi trên đoạn;a b .4. Định lý mở rộng Giả sử hàm sốfcó đạo hàm trên khoảngI.•Nếu'( ) 0f x≥vớix I∀ ∈và'( ) 0f x=chỉ tại một số hữu hạn điểm thuộcIthì hàm sốfđồng biến trên khoảngI;•Nếu'( ) 0f x≤vớix I∀ ∈và'( ) 0f x=chỉ tại một số hữu hạn điểm thuộcIthì hàm sốfnghịch biến trên khoảngI.1.2 DẠNG TOÁN THƯỜNG GẶPDạng 1 : Xét chiều biến thiên của hàm số .Xét chiều biến thiên của hàm số()y f x= ta thực hiện các bước sau: •Tìm tập xác địnhDcủa hàm số .•Tính đạo hàm()’ ‘y f x= . •Tìm các giá trị củaxthuộcDđể()’ 0f x=hoặc()’f xkhông xác định( ta gọi đó là điểm tới hạn hàm số ).•Xét dấu()’ ‘y f x= trên từng khoảng xthuộcD.•Dựa vào bảng xét dấu và điều kiện đủ suy ra khoảng đơn điệu của hàm số. Ví dụ 1: Xét chiều biến thiên của các hàm số sau: 21.1xyx+=−22 12.2x xyx − + −=+Giải:21.1xyx+=−*Hàm số đã cho xác định trên khoảng()();1 1;−∞ ∪ +∞.*Ta có:( )23′ 0, 11y xx-= ∀ ≠−*Bảng biến thiên: x−∞1+∞’y−−y1 −∞+∞1
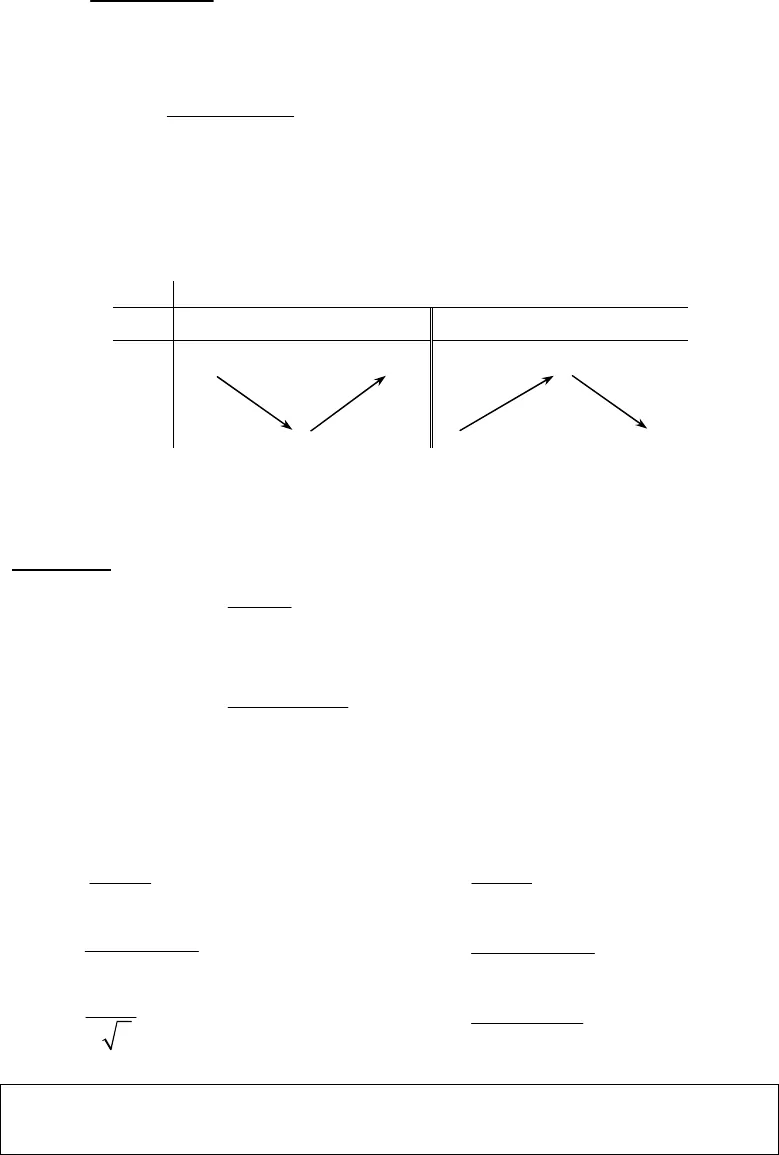Nguyễn Phú Khánh – Đà Lạt Tài Liệu ôn thi Tú Tài Đại học theo cấu trúc BGD.7Vậy hàm số đồng biến trên mỗi khoảng();1−∞ và ()1;+∞.22 12.2x xyx − + −=+*Hàm số đã cho xác định trên khoảng()(); 2 2;−∞ − ∪ − +∞.*Ta có:( )224 5′ , 22x xy xx− − += ∀ ≠ −+5′ 01xyx= −= ⇔=*Bảng biến thiên :x−∞5−2−1+∞’y−0+ +0−y+∞+∞−∞−∞Vậy, hàm số đồng biến trên các khoảng()5; 2− −và()2;1− , nghịch biến trên các khoảng(); 5−∞ −và()1;+∞.Nhận xét: * Đối với hàm số( . 0)ax by a ccx d+= ≠+luôn đồng biến hoặc luôn nghịchbiến trên từng khoảng xác định của nó.* Đối với hàm số2′ ‘ax bx cya x b+ +=+luôn có ít nhất hai khoảng đơn điệu.* Cả hai dạng hàm số trên không thể luôn đơn điệu trênℝ.Bài tập tương tự :Xét chiều biến thiên của các hàm số sau:2 11.1xyx −=+24 32.2x xyx+ +=+ 13.3xyx+= 234.1xyx=+ 224 35.2 2 4x xyx x− +=− − 222 26.2 1x xyx x+ +=+ + Ví dụ 2: Xét chiều biến thiên của các hàm số sau: 3 21. 3 24 26y x x x= − − + + 4 22. 6 8 1y x x x= − + +
admincd
Trả lời Hủy
- Assign a menu in Theme Options > Menus
-
Newsletter
WooCommerce not Found
