Download.vn Học tập Lớp 10

Bạn đang đọc: Chuyên đề phương trình đại số

Chuyên đề phương trình đại số Chuyên đề phương trình, bất phương trình và hệ phương trình đại số

Giới thiệu Tải về Bình luận

• 1

Mua tài khoản Download Pro để trải nghiệm website Download.vn KHÔNG quảng cáo & tải File cực nhanh chỉ từ 79.000đ. Tìm hiểu thêm Mua ngay

Nhằm đem đến cho các bạn có thêm nhiều tài liệu học tập Download.vn xin giới thiệu tài liệu Chuyên đề phương trình đại số lớp 10.

Đây là tài liệu cực kì hữu ích, gồm 23 trang trình bày đầy đủ các dạng toán phương trình, bất phương trình và hệ phương trình với các bài toán được giải chi tiết. Hy vọng với tài liệu này các bạn học sinh lớp 10 có thêm nhiều tài liệu tham khảo, củng cố kiến thức để đạt được điểm cao trong các bài thi học kì 1, kì 2. Mời các bạn cùng tham khảo và tải tài liệu tại đây.

Chuyên đề phương trình đại số

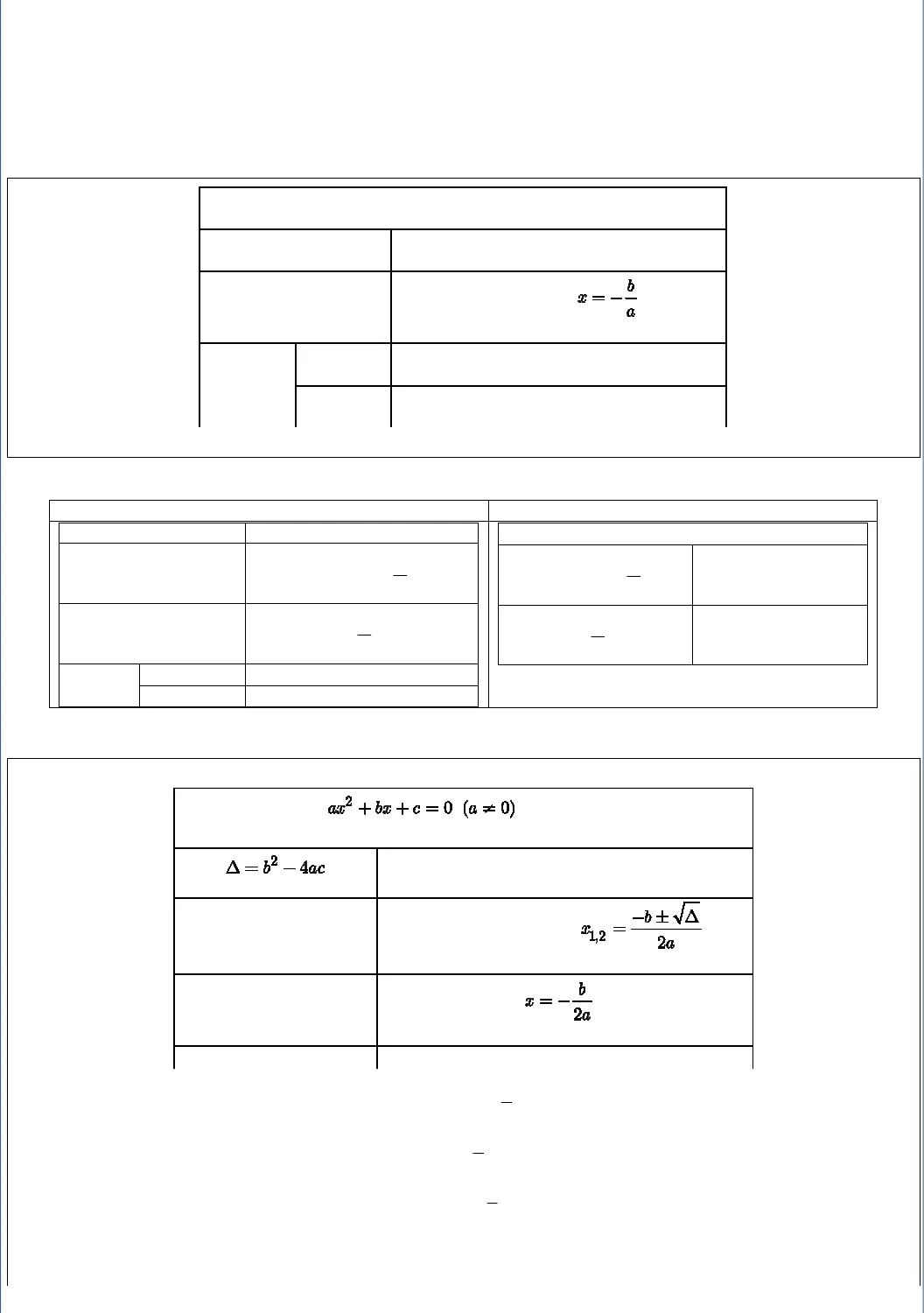GV.Lưu Huy Thưởng 0968.393.899 BỂ HỌC VÔ BỜ – CHUYÊN CẦN SẼ ĐẾN BẾN Page 1 CHUYÊN ĐỀ PHƯƠNG TRÌNH VÀ BẤT PHƯƠNG TRÌNHBÀI 1: ĐẠI CƯƠNG VỀ PHƯƠNG TRÌNH VÀ BẤT PHƯƠNG TRÌNHI. KIẾN THỨC CẦN NHỚ1. PHƯƠNG TRÌNH DẠNG:0ax b+ = Chú ý: Khi a ≠0 thì (1) được gọi là phương trình bậc nhất một ẩn.2. BẤT PHƯƠNG TRÌNH DẠNG0ax b+ Dấu nhị thức bậc nhấtĐiều kiện Kết quả tập nghiệm a > 0S =ba; −∞ −  a − +∞  a = 0b≥0 S = ∅b S = Rf(x) = ax + b (a≠0)x∈ba; −∞ −  a.f(x) − +∞  a.f(x) > 03. PHƯƠNG TRÌNH BẬC HAI:20ax bx c+ + =1. Cách giải Chú ý: – Nếu a + b + c = 0 thì (1) có hai nghiệm là x = 1 và x = ca. – Nếu a – b + c = 0 thì (1) có hai nghiệm là x = –1 và x =ca−. – Nếu b chẵn thì ta có thể dùng công thức thu gọn với2bb′=.2. Định lí Vi–et Hai số1 2,x xlà các nghiệm của phương trình bậc hai20ax bx c+ + =khi và chỉ khi chúng thoả mãn các hệ thức ax + b = 0 (1) Hệ số Kết luậna≠0(1) có nghiệm duy nhất a = 0b≠0(1) vô nghiệm b = 0 (1) nghiệm đúng với mọi x (1)Kết luận∆> 0(1) có 2 nghiệm phân biệt ∆= 0(1) có nghiệm kép ∆vô nghiệm GV.Lưu Huy Thưởng 0968.393.899 BỂ HỌC VÔ BỜ – CHUYÊN CẦN SẼ ĐẾN BẾN Page 2 1 2bS x xa= + = −và1 2cP x xa= =. 4. BẤT PHƯƠNG TRÌNH BẬC HAIXét dấu tam thức bậc hai Giải bất phương trình bậc haif(x) =2ax bx c+ +(a≠≠≠≠0)∆ a.f(x) > 0,∀x∈R∆= 0a.f(x) > 0,∀x∈2bRa    −   ∆> 0a.f(x) > 0,∀x∈(–∞; x1)∪(x2;+∞)a.f(x) ấu tam thức bậc hai để giảiII. CÁC DẠNG TOÁN 1. Dạng toán 1: Giải và biện luận phương trình và bất phương trìnhHT1. Giải và biện luận các phương trình sau theo tham số m: 1)2( 2) 2 3m x m x+ − = − 2)( ) 2m x m x m− = + − 3)( 3) ( 2) 6m x m m x− + = − + 4)2( 1) (3 2)m x m x m− + = − 5)2 2( ) 2 1m m x x m− = + − 6)2( 1) (2 5) 2m x m x m+ = + + +HT2. Giải các bất phương trình sau: 1)(2 5)( 2)04 3x xx− +>− + 2)3 51 2x xx x− +>+ − 3)3 1 25 3x xx x− − − 4)3 412xx−>− 5)2 512xx−≥ −− 6)2 51 2 1x x≤− −HT3. Giải và biện luận các bất phương trình sau: 1)( ) 1m x m x− ≤ − 2)6 2 3mx x m+ > + 3)( 1) 3 4m x m m+ + + 4)21mx m x+ > + 5)( 2)16 3 2m xx m x−− ++ > 6)23 2( ) ( 1)mx x m m− − − +HT4. Giải và biện luận các bất phương trình sau: 1)2 101x mx+ −>+ 2)101mx mx− + 3)1( 2) 0x x m− − + >HT5. Giải và biện luận các phương trình sau: 1)25 3 1 0x x m+ + − = 2)22 12 15 0x x m+ − = 3)2 22( 1) 0x m x m− − + = 4)2( 1) 2( 1) 2 0m x m x m+ − − + − = 5)2( 1) (2 ) 1 0m x m x− + − − = 6)22( 3) 1 0mx m x m− + + + =HT6. Giải và biện luận các bất phương trình sau: 1)23 0x mx m− + + > 2)2(1 ) 2 2 0m x mx m+ − + ≤ 3)22 4 0mx x− + >HT7. Trong các phương trình sau, tìm giá trị của tham số để phương trình: i) Có nghiệm duy nhất ii) Vô nghiệm iii) Nghiệm đúng với mọi x ∈ R. GV.Lưu Huy Thưởng 0968.393.899 BỂ HỌC VÔ BỜ – CHUYÊN CẦN SẼ ĐẾN BẾN Page 3 1)( 2) 1m x n− = − 2)2( 2 3) 1m m x m+ − = −3)2( 2)( 1) ( )mx x mx m x+ + = + 4)2 2( ) 2 1m m x x m− = + −HT8. Tìm m để các bất phương trình sau vô nghiệm: a)2 24 3m x m x m+ − + b)21 (3 2)m x m m x+ ≥ + − c)24mx m mx− > − d)23 2( ) ( 1)mx x m m− − − +2. Dạng toán 2: Dấu của nghiệm số phương trình bậc hai20 ( 0) (1)ax bx c a+ + = ≠•(1) có hai nghiệm trái dấu⇔P •(1) có hai nghiệm cùng dấu⇔00P∆ ≥>•(1) có hai nghiệm dương⇔000PS∆ ≥>> •(1) có hai nghiệm âm⇔000PS∆ ≥> Trong các trường hợp trên nếu yêu cầu hai nghiệm phân biệt thì ∆> 0.Bài tậpHT9. Xác định m để phương trình: i) có hai nghiệm trái dấu ii) có hai nghiệm âm phân biệt iii) có hai nghiệm dương phân biệt 1)25 3 1 0x x m+ + − = 2)22 12 15 0x x m+ − = 3)2 22( 1) 0x m x m− − + = 4)2( 1) 2( 1) 2 0m x m x m+ − − + − = 5)2( 1) (2 ) 1 0m x m x− + − − = 6)22( 3) 1 0mx m x m− + + + = 7)24 1 0x x m− + + = 8)2( 1) 2( 4) 1 0m x m x m+ + + + + =3. Dạng toán 3: Áp dụng định lý Vieta. Biểu thức đối xứng của các nghiệm số Ta sử dụng công thức1 2 1 2;b cS x x P x xa a= + = − = =để biểu diễn các biểu thức đối xứng của các nghiệm x1, x2theo S và P. Ví dụ:2 2 2 21 2 1 2 1 2( ) 2 2x x x x x x S P+ = + − = − 3 3 2 21 2 1 2 1 2 1 2( ) ( ) 3 ( 3 )x x x x x x x x S S P + = + + − = −   b. Hệ thức của các nghiệm độc lập đối với tham số Để tìm hệ thức của các nghiệm độc lập đối với tham số ta tìm: 1 2 1 2;b cS x x P x xa a= + = − = = (S, P có chứa tham số m). Khử tham số m giữa S và P ta tìm được hệ thức giữa x1và x2.c. Lập phương trình bậc hai Nếu phương trình bậc hai có các nghiệm u và v thì phương trình bậc hai có dạng: 20x Sx P− + =, trong đó S = u + v, P = uv.Bài tậpHT10. Gọi 1 2,x xlà các nghiệm của phương trình. Không giải phương trình, hãy tính: