Download.vn Học tập Lớp 11 Toán 11
Bạn đang đọc: Chuyên đề vectơ trong không gian, quan hệ vuông góc
Chuyên đề vectơ trong không gian, quan hệ vuông góc Tài liệu ôn tập môn Toán lớp 11
Giới thiệu Tải về Bình luận
- 1
Mua tài khoản Download Pro để trải nghiệm website Download.vn KHÔNG quảng cáo & tải File cực nhanh chỉ từ 79.000đ. Tìm hiểu thêm Mua ngay
Nhằm mang đến cho học sinh lớp 11 có thêm nhiều tài liệu học chương trình Hình học 11 chương 3, Download.vn xin giới thiệu tài liệu Chuyên đề vectơ trong không gian, quan hệ vuông góc.
Tài liệu gồm 99 trang với đầy đủ lý thuyết, dạng toán và bài tập chủ đề vectơ trong không gian, quan hệ vuông góc, sẽ giúp các em dễ dàng tiếp cận và học tốt hơn hình học không gian. Sau đây là nội dung chi tiết mời các em cùng tham khảo và tải tài liệu tại đây.
Chuyên đề vectơ trong không gian, quan hệ vuông góc
GV. TRGV. TRGV. TRGV. TRẦẦẦẦN QUN QUN QUN QUỐỐỐỐC NGHC NGHC NGHC NGHĨAĨAĨAĨA 1111VÉCTƠ TRONG KHÔNG GIANQUAN HỆ VUÔNG GÓCVấn đề 1. VÉCTƠ TRONG KHÔNG GIANI. Véctơtrongkhônggian①①①① Véctơ, giá và độ dài của véctơ. Véctơ trong không gian là một đoạn thẳng có hướng. Kí hiệu ABchỉ véctơ có điểm đầu A, điểm cuốiB. Véctơ còn được kí hiệua,b,c, … Giá của véctơ là đường thẳng đi qua điểm đầu và điểm cuối của véctơ đó. Hai véctơ được gọi là cùng phương nếu giá của chúng song song hoặc trùng nhau. Ngược lại, hai véctơ có giá cắt nhau được gọi là hai véctơ không cùng phương. Hai véctơ cùng phương thì có thể cùng hướng hoặc ngược hướng. Độ dài của véctơ là độ dài của đoạn thẳng có hai đầu mút là điểm đầu và điểm cuối của véctơ. Véctơ có độ dài bằng 1 gọi là véctơ đơn vị. Kí hiệu độ dài véctơ ABlàABNhư vậy: AB AB BA= =.②②②② Hai véctơ bằng nhau, đối nhau. Cho hai véctơ a,b(≠0) Hai véctơ avàbđược gọi là bằng nhau nếu chúng có cùng hướng và cùng độ dài. Kí hiệua b=và| | | |a ba ba b= ⇔=cuøng höôùng Hai véctơ avà được gọi là đối nhau nếu chúng ngược hướng và cùng độ dài. Kí hiệua b= −và| | | |a ba ba b= ⇔=cuøng höôùng③③③③ Véctơ – không. Véctơ – không là véctơ có điểm đầu và điểm cuối trùng nhau. Kí hiệu:0,… 0AA BB CC= = = = .Véctơ – không có phương, hướng tùy ý, có độ dài bằng không. Véctơ – không cùng phương, cùng hướng với mọi véctơ. II.Phépcộngvàphéptrừvéctơ①①①① Định nghĩa 1. Cho avàb. Trong không gian lấy một điểm A tùy ý, dựng AB a=,BC b=. VéctơACđược gọi là tổng của hai véctơ avàbvà được kí hiệu AC AB BC a b= + = + . ()a b a b− = + − ②②②② Tính chất 1. Tính chất giao hoán: a b b a+ = + Tính chất kết hợp: ()()a b c a b c+ + = + + Cộng với 0: 0 0a a a+ = + = Cộng với véctơ đối: ()0a a a a+ − = − + = abABCaba b+8Chủđề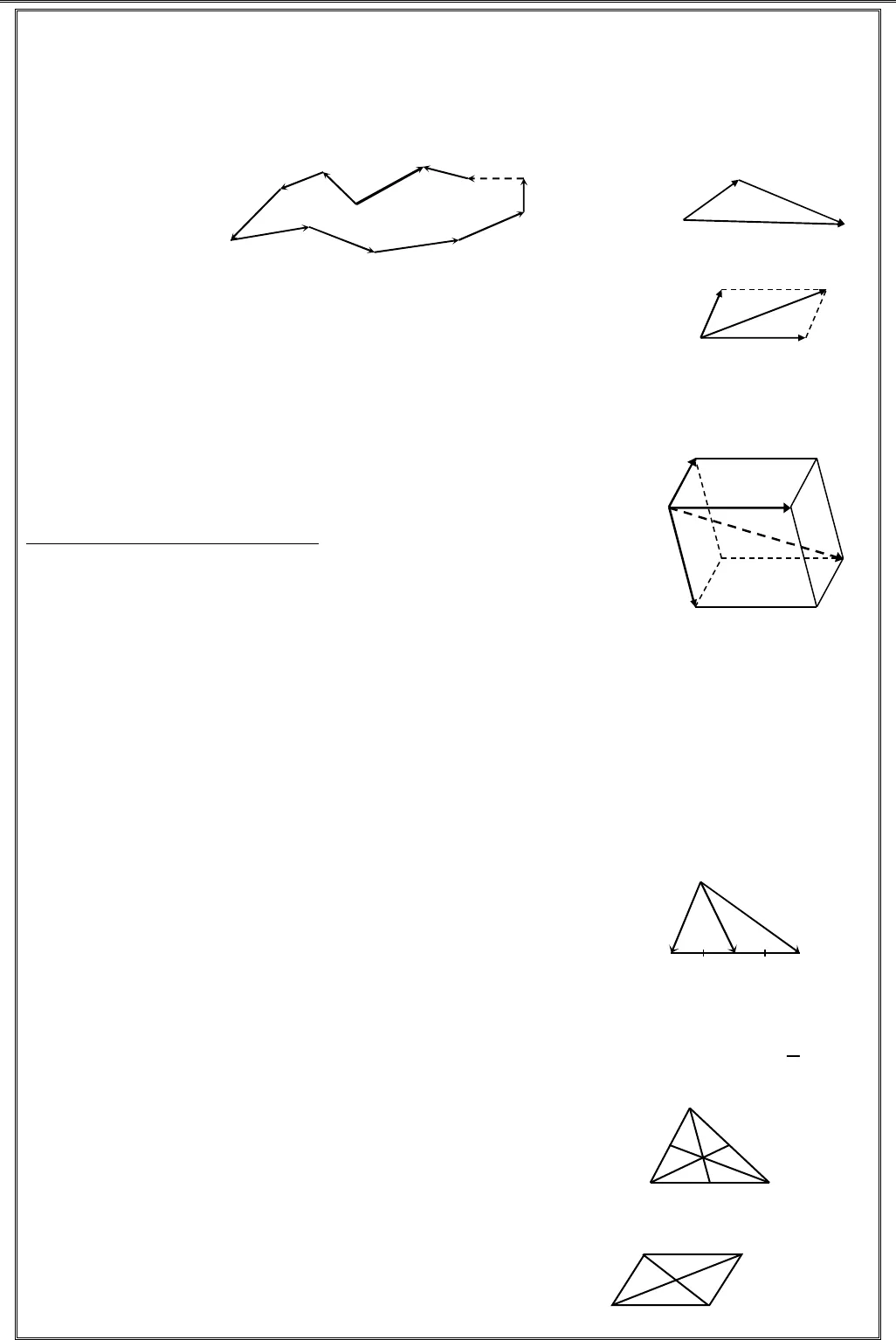
TÀI LITÀI LITÀI LITÀI LIỆỆỆỆU HU HU HU HỌỌỌỌC TC TC TC TẬẬẬẬP TOÁN 11P TOÁN 11P TOÁN 11P TOÁN 11––––HK2HK2HK2HK2 2222③③③③ Các qui tắc. Qui tắc ba điểm: Với ba điểm A,B,Cbất kì ta có: AC AB BC= + Mở rộng: Qui tắc đa giác khép kín Chonđiểm bất kì 1 2 3 –1, , , , , n nA A A A A…. Ta có:1 2 2 3 1 1n n nA A A A A A A A−+ + + = … Qui tắc trừ (ba điểm cho phép trừ): Với ba điểmA,B,Cbất kì ta có: AC BC BA= − Qui tắc hình bình hành: Với hình bình hànhABCDta có:AC AB AD= + vàDB AB AD= − Qui tắc hình hộp. Cho hình hộp .ABCD A B C D′ ′ ′ ′với AB,AD,AA′là ba cạnhcó chung đỉnhA vàAC′ là đường chéo, ta có:AC AB AD AA′ ′= + + III.Phépnhânmộtsốvớimộtvéctơ①①①① Định nghĩa 2. Cho0k≠và véctơ0a≠. Tích.k alà một véctơ: – Cùng hướng với anếu 0k>- Ngược hướng với anếu 0k②② Tính chất 2. Với a,bbất kì; ,m n R∈, ta có: ()m a b ma mb+ = + ()m n a ma na+ = + ()()m na mn a= 1.a a= ,()1 .a a− = − 0. 0a=;.0 0k= ③③③③ Điều kiện để hai véctơ cùng phương. Cho hai véctơavàb(0≠),0k≠:acùng phươngb⇔a kb=Hệ quả: điều kiện để ba điểm A,B,Cthẳng hàng làAB k AC= ④④④④ Một số tính chất. Tính chất trung điểm Cho đoạn thẳngABcóIlà trung điểm, ta có: 0IA IB+ = ;IA IB= − ;12AI IB AB= = 2MA MB MI+ = (Mbất kì) Tính chất trọng tâm. ChoABC∆,Glà trọng tâm, ta có:0GA GB GC+ + = 3MA MB MC MG+ + = (Mbất kì) Tính chất hình bình hành. Cho hình bình hànhABCDtâmO, ta có: 0OA OB OC OD+ + + = 4MA MB MC MD MO+ + + = 1A2A3A4A5A7A8A9A10An-1AnAABCABCDABCDA’B’C‘D’MAIBABCGABCDO
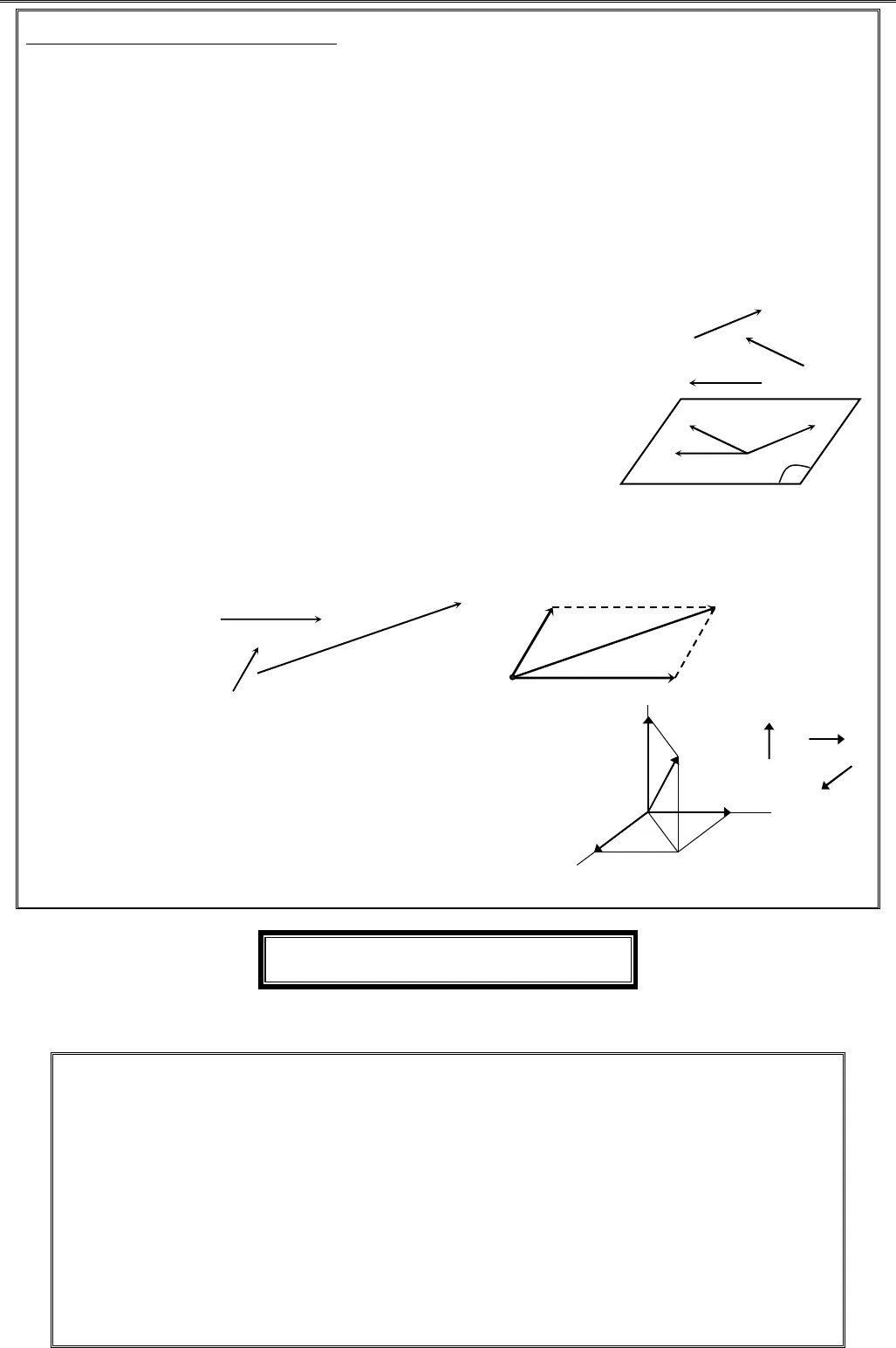GV. TRGV. TRGV. TRGV. TRẦẦẦẦN QUN QUN QUN QUỐỐỐỐC NGHC NGHC NGHC NGHĨAĨAĨAĨA 3333IV.Điềukiệnđểbavéctơđồngphẳng①①①① Khái niện về sự đồng phẳng của ba véctơ trong không gian. Cho ba véctơa,b,c (≠ 0) trong không gian. Từ một điểm O bất kì ta dựng OA a=,OB b=,OC c=. Khi đó xảy ra hai trường hợp: Các đường thẳng OA,OB,OCkhông cùng nằm trong một mặt phẳng thì ta nói ba véctơ a,b,ckhông đồng phẳng. Các đường thẳng OA,OB,OC cùng nằm trong một mặt phẳng thì ta nói ba véctơ a,b,cđồng phẳng. ②②②② Định nghĩa 3. Ba véctơ gọi là đồng phẳng nếu các giá của chúng cùng song song với một mặt phẳng.Trên hình bên, giá của các véctơa,b,ccùng song song với mặt phẳng (α) nên ba véctơ a,b,cđồng phẳng.③③③③ Điều kiện để ba véctơ đồng phẳng Định lí 1. Cho ba véctơa,b,c trong đó a vàb không cùng phương. Điều kiện cần và đủ để ba véctơa,b,cđồng phẳng là có duy nhất các số m,nsao choc ma nb= + .④④④④ Phân tích một véctơ theo ba véctơ không đồng phẳng Định lí 2. Nếu ba véctơa,b,c không đồng phẳng thì với mỗi véctơd, ta tìm được duy nhất các sốm,n,psao chod ma nb pc= + + .Dạng1.TínhtoánvéctơA. PHƯƠNG PHÁP GIẢI ①①①① Quy tắc ba điểm: AB AC CB= + (quy tắc cộng)AB CB CA= − (quy tắc trừ)②②②② Quy tắc hình bình hành: Với hình bình hành ABCDta luôn có:AC AB AD= + ③③③③ Quy tắc hình hộp: Cho hình hộp .ABCD A B C D′ ′ ′ ′, ta được:AC AB AD AA′ ′= + + ④④④④ Quy tắc trung điểm: Cho I là trung điểmAB,M là điển bất kỳ: 0IA IB+ = và2MA MB MI+ = ⑤⑤⑤⑤ Tính chất trọng tâm của tam giác: Glà trọng tâmABC∆,M∀ta có:0GA GB GC+ + = và 3MA MB MC MG+ + = abcOOBAcm.an.babcOAmanbpcdD’DOCABabcα