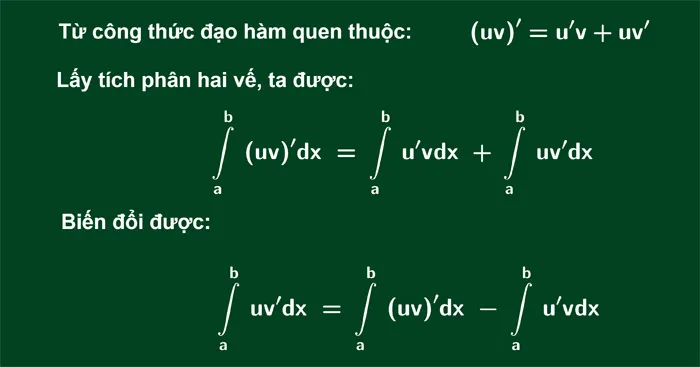Công thức Tích phân là những công thức quan trọng giúp các em lớp 12 ghi nhớ để vận dụng tính toán nhanh nhất các bài toán liên quan đến tích phân và cho ra kết quả chính xác.
Bạn đang đọc: Công thức Tích phân: Lý thuyết và bài tập
Trong kì thi THPT Quốc gia môn Toán thì số lượng công thức cần ghi nhớ là không hề nhỏ. Đối với các bài thi trắc nghiệm, điều cần thiết là các em học sinh cần nắm kiến thức rộng và có phương pháp giải nhanh hiệu quả để có thể ghi điểm nhiều nhất. Dưới đây tổng hợp toàn bộ kiến thức về dấu tích phân, bảng tích phân, ứng dụng kèm theo một số dạng bài tập. Hi vọng tài liệu này sẽ là người bạn đồng hành cùng các em trên con đường chinh phục 9+ môn Toán. Bên cạnh cách tính tích phân các bạn xem thêm bộ đề ôn thi THPT Quốc gia môn Toán, phân dạng câu hỏi và bài tập trong đề thi THPT Quốc gia môn Toán.
Công thức tích phân đầy đủ, chính xác nhất
I. Lý thuyết Tích phân
1. Tích phân là gì?
Là phép lấy tích phân là cách ta muốn biểu diễn quy trình ngược lại của phép lấy đạo hàm.
Ví dụ: Nếu ta biết rằng: và ta muốn biết hàm số nào đã đạo hàm ra được hàm số này?
Ta có là một nguyên hàm của
. Ngoài ra ta còn vô số nguyên hàm khác, chẳng hạn như:
Tổng quát, ta nói
là tích phân bất định (hay nguyên hàm) của
. Con số ? được gọi là hằng số tích phân.
2. Dấu tích phân
Ký hiệu ∫ hình thành bởi sự kéo dài ký tự “?” viết tắt của chữ “sum” (tổng) (Người Đức, Anh thời xưa viết chữ “?” giống với ký hiệu tích phân bây giờ). ∑ là ký hiệu của “tổng”. Nó được dùng cho tổng hữu hạn hay vô hạn. ∫ là ký hiệu của tổng hữu hạn các diện tích vô cùng nhỏ (hoặc các biến vô cùng nhỏ khác). Ký hiệu chữ “?” dài này được Lebniz giới thiệu khi ông phát triển một số khái niệm của tích phân.
3. Tích phân hằng số
(? và ? là các hằng số).
4. Tích phân lũy thừa của ?
Công thức này đúng khi ? ≠ −1. Khi tích phân lũy thừa của ?, ta thêm 1 vào lũy thừa và chia biến lũy thừa mới cho giá trị lũy thừa mới.
II. Bảng tích phân
1. Tích phân cơ bản
2. Tích phân từng phần
Công thức tính tích phân từng phần:
Theo qui tắc lấy đạo hàm một tích:
Lấy tích phân cả hai vế ta được:
Từ đây ta có công thức sau:
3. Tích phân lượng giác
Giả sử ta cần tính tích phân
trong đó R là hàm hữu tỉ của hai đối số. Ta có thể hữu tỉ hoá tích phân trên bằng cách đặt .
Thật vậy:
Do đó, có thể đưa ra tích phân I về dạng:
4. Tích phân xác định
Cách tính tích phân xác định:
- ?(?) là nguyên hàm của ?(?).
- ?(?) là giá trị nguyên hàm ứng với cận trên ? = ?.
- ?(?) là giá trị nguyên hàm ứng với cận dưới ? = ?.
Biểu thức này gọi là tích phân xác định.
5. Tích phân không xác định
Họ tất cả các nguyên hàm của hàm f trên một khoảng I nào đó được gọi là tích phân không xác định của hàm này trên khoảng I và được kí hiệu là f (x) dx:
trong đó A là hằng số
6. Tích phân hàm số hữu tỉ
Các phân thức hữu tỉ đơn giản nhất là các phân thức có dạng
trong đó A,M,N,p,q là các số thực, k = 2,3,4…, còn tam thức bậc hai không có nghiệm thực, tức là . Bây giờ ta hãy khảo sát tích phân các phân thức hữu tỉ trên:
a) Dạng I:
b) Dạng II:
c) Dạng III:
Ta xét tích phân thứ hai ở vế phải. Đặt
Ta có:
d) Dạng IV:
III. Ứng dụng tích phân
1. Ứng dụng Công
Trong vật lý, công được hình thành khi một lực tác động vào một vật và gây ra sự dịch chuyển, ví dụ như lái xe đạp.
Nếu có một lực biến thiên, thay đổi, ta dùng tích phân để tính công sinh ra bởi lực này. Ta dùng: với F(x) là lực.
2. Ứng dụng giá trị trung bình
Giá trị trung bình của hàm ?(?) trong miền ? = ? đến ? = ? được xác định bởi: Trung bình =
3. Ứng dụng quãng đường
Nếu ta biết biểu thức vận tốc ? theo thời gian ?, ta có thể biết quãng đường ? của một vật thể khi đi từ thời gian ? = ? đến ? = ? bằng tích phân như sau:
Chú ý: Bạn có thể thấy từ những ứng dụng của tích phân trong công, tính giá trị trung bình, tính quãng đường, tích phân xác định không chỉ đơn thuần dùng để tích diện tích dưới đường cong.
IV. Bài tập tích phân
Câu 1: Cho f(x) là hàm số liên tục trên đoạn [a ; b] và Tìm mệnh đề đúng
trong các mệnh đề sau.
Câu 2: Cho hàm số y=f(x) liên tục trên khoàng K và a, b, c in K. Mệnh đề nào sau đây sai?
Câu 3: Cho hàm số f(t) liên tục trên K và a,, F(t) là một nguyên hàm của f(t) trên K. Chọn khẳng định sai trong các khẳng định sau.
Câu 4: Cho hai tích phân và
. Giá trị của tích phân
là:
A. m-n.
B. n-m.
C. m+n.
D. Không thể xác định.
Câu 5: Cho tích phân và
. Tích phân
có giá trị là:
A. m+n.
B. m-n
C. -m-n.
D. Không thể xác định.
Câu 6: Tích phân được phân tích thành:
Câu 7: Cho . Tính tích phân
A. -9.
B. -3.
C. 3 .
D. 5 .