ĐỀ THI TUYỂN SINH SAU ĐẠI HỌC VIỆN TOÁN HỌC ĐỢT THÁNG 9 – 2012
Bạn đang đọc: Đề thi cao học Viện Toán năm 2012 – Môn thi: Đại số và Giải tích
MÔN THI: GIẢI TÍCH
Câu 1: Chứng minh rằng phương trình:
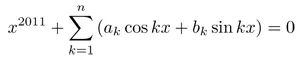
Có it nhất một nghiệm thuộc đoạn [-π, π], n là một số nguyên dương
Câu 2: Tìm cực trị của hàm số:
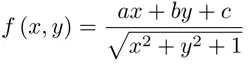
theo a, b, c, biết rằng c # 0
Câu 3: Xét sự hội tụ đều của chuỗi hàm:
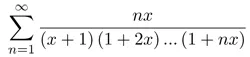trong miền [0; ε], ε > 0
Câu 4: Cho (X, d1), (Y, d2) là các không gian metric và A là một tập hợp hoàn toàn bị chặn trong X. Chứng minh rằng nếu ánh xạ f: X -> Y liên tục đều trên X thì f(A) là tập hợp bị chặn trong Y.
Câu 5: Giả sử A là một toán tử tuyến tính giới nội từ không gian tuyến tính định chuẩn X vào không gian tuyến tính định chuẩn Y và A* là toán tử liên hợp của nó. Chứng minh rằng:
a. Nếu A* là một toàn ánh thì A là một đơn ánh
b. Nếu A* là một đơn ánh thì A(X) là một tập trù mật trong Y
Câu 6: Giả sử {en} là một có ở trực chuẩn trong không gian Hilbert H. Y là một không gian Banach, A : H –> Y là một toán tử tuyến tính giới nội và chuỗi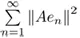 
hội tụ. Chứng minh rằng A là một toán tử compact.
MÔN THI: ĐẠI SỐ
Bài 1: Trong không gian R3 cho hệ vecto S = {x1 = (1; k; 5), x2 = (2; – 1; k), z = (3; -1; 3)}
1. Xét tính độc lập tuyến tính và phụ thuộc tuyến tính của hệ trên theo tham số k.
2. Cho k = 2; Hãy xét xem hệ vecto b = (2; 3; 4) có thuộc không gian con sinh bởi hệ S không?
Bài 2: Cho ánh xạ tuyến tính f: X–>Y
1. Chứng minh rằng ảnh của một hệ phụ thuộc tuyến tính thì phụ thuộc tuyến tính. Kết luận tương tự với hệ độc lập tuyến tính có đúng không? Giải thích?
2. Nếu X và Y là những không gian vecto có cùng số chiều hữu hạn thì f là đơn cấu khi và chỉ khi nó là toàn cấu
Bài 3: Cho X là một nhóm xyclic hữu hạn cấp n
1. Chứng minh rằng mọi nhóm con của X đều là xyclic.
2. Chứng minh rằng X đẳng cấu với nhóm cộng Zn
Download tài liệu để xem thêm chi tiết
