Đề thi chọn đội tuyển học sinh giỏi Toán lớp 12 năm 2011 – 2012

ĐỀ CHÍNH THỨC

Bài 1: (4 điểm)
Giải hệ phương trình sau:

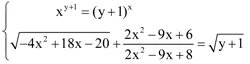
Bài 2: (4 điểm)
Cho hai đường tròn và cắt nhau tại A và B. Trên tia đối của tia AB lấy điểm M. Cát tuyến qua B cắt (O₁) và (O₂) lần lượt tại C và D (B nằm giữa C và D). Đường thẳng MC cắt (O₁) tại P khác C. Đường thẳng MD cắt (O₂) tại Q khác D. Gọi O là tâm đường tròn ngoại tiếp tam giác ACD, E là giao điểm của PB và AC, F là giao điểm của QB và AD. Chứng minh rằng MO vuông góc với EF .

Bài 3: (4 điểm)
Cho a, b, c là các số thực dương, chứng minh rằng:

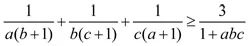
Bài 4: (4 điểm)
Cho đa thức P(x) = x²⁰¹² – mx²⁰¹⁰ + m (m#0). Giả sử P(x) có đủ 2012 nghiệm thực. Chứng minh rằng trong các nghiệm của P(x) có ít nhất một nghiệm x₀ thoả mãn |x₀|

Bài 5: (4 điểm)
Cho các số nguyên x, y. Biết rằng: x² – 2xy + y² – 5x + 7y và x² – 3xy + 2y² + x – y đều chia hết cho 17.
Chứng minh rằng: xy – 12x + 15y chia hết cho 17.

Download tài liệu để xem thêm chi tiết