| BỘ GIÁO DỤC VÀ ĐÀO TẠO ĐỀ THI CHÍNH THỨC |
KỲ THI CHỌN HỌC SINH GIỎI QUỐC GIA THPT NĂM 2013 MÔN: TOÁN Thời gian: 180 phút (không kể thời gian giao đề) Ngày thi thứ nhất: 11/01/2013 |
Bài 1: Giải hệ phương trình (5 điểm)
Bạn đang đọc: Đề thi chọn học sinh giỏi Quốc gia THPT môn Toán năm 2013 – Ngày thứ nhất
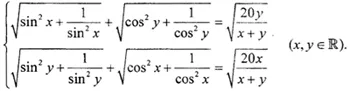
Bài 2: (5 điểm) Cho dãy số thực (an) xác định bởi:
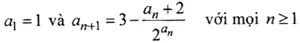
Chứng minh rằng dãy (an) có giới hạn hữu hạn. Hãy tìm giới hạn đó
Bài 3: (5 điểm). Cho tam giác không cân ABC. Ký hiệu (I) là đường tròn tâm I nội tiếp tam giác ABC và D, E, F lần lượt là tiếp điểm của đường tròn (I) với các cạnh BC, CA, AB. Đường thẳng đi qua E và vuông góc với BI cắt (I) tại K (K#E), đường thẳng đi qua F và vuông góc với CI cắt (I) tại L (L # F). Gọi J là trung điểm của KL.
a. Chứng minh rằng D, I, J thẳng hàng
b. Giả sử các đỉnh B và C cố định, đỉnh A thay đổi sao cho tỷ số AB/AC = k (k không đổi). Gọi M, N tương ứng là các giao điểm của IE, IF với (I) (M # E, N # F). MN cắt IB, IC lần lượt tại P, Q. Chứng minh rằng trung trực của PQ luôn đi qua một điểm cố định.
Bài 4: (5 điểm). Cho trước một số tự nhiên được viết trên một đường thẳng. Ta thực hiện các bước điền số lên đường thẳng như sau: tại mỗi bước, trước tiên xác định tất cả các cặp số kề nhau hiện có trên đường thẳng theo thứ tự từ trái qua phải, sau đó điền vào giữa mỗi cặp một số bằng tổng của hai số thuộc cặp đó. Hỏi sau 2013 bước, số 2013 xuất hiện bao nhiêu lần trên đường thẳng trong các trường hợp sau:
a. Các số cho trước là: 1 và 1000?
b. Các số cho trước là: 1, 2, …, 1000 và được xếp theo thứ tự tăng dần từ trái qua phải?
Download tài liệu để xem thêm chi tiết

