Đề thi học sinh giỏi giải toán trên máy tính cầm tay năm học 2011

(Đề thi chính thức)

(Thời gian làm bài 90 phút không kể thời gian giao đề)
Ngày thi: 05/02/2012

Chú ý:

– Các giá trị phải tính ra số thập phân, lấy chính xác 5 chữ số thập phân không làm tròn.

– Thí sinh phải ghi tóm tắt cách giải hay công thức tính.

Câu 1.

Biết x, y là nghiệm của hệ phương trình: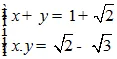

Tính giá trị biểu thức A = x³ + y³

Câu 2.

Tìm ba số thực a, b, c biết Parabol (P): y = ax² + bx + c có đỉnh nằm trên trục hoành và đi qua hai điểm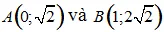

Câu 3.

Cho tam giác ABC, gọi M là điểm xác định bởi BM = BC – 3AB, N là điểm xác định bởi CN = m.AC -BC. Tìm giá trị m để ba điểm A, M, N thẳng hàng.

Câu 4.

Giải phương trình: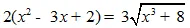

Câu 5.

Cho tam giác ABC có độ dài ba đường trung tuyến bằng 15; 18; 21. Tính diện tích của tam giác ABC.

Câu 6.

Cho đa thức f(x) = x5 + x2 + 1 có năm nghiệm x₁, x₂, x₃, x₄, x₅

Kí hiệu p(x) = x² – 81. Hãy tìm tích A = p(x₁).p(x₂).p(x₃).p(x₄).p(x₅)

Câu 7.

Giải hệ phương trình: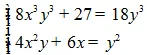

Câu 8.

Cho tam giác ABC có chu vi 58cm, góc B = 57⁰18′, góc C = 82⁰35′ . Tính cạnh BC.

Câu 9.

Tính giá trị gần đúng của biểu thức:

Câu 10.

Cho ba số thực a, b, c đều dương và thỏa mãn điều kiện a+b+c=1. Hãy tìm giá trị lớn nhất của biểu thức P = abc(a+b)(b+c)(c+a).

Download tài liệu để xem thêm chi tiết

Đề thi học sinh giỏi giải toán trên máy tính cầm tay năm học 2011 – 2012 môn Toán khối 10