Đề thi học sinh giỏi lớp 9 THCS tỉnh Quảng Bình môn Toán (năm học 2010 – 2011)

Câu 1: (2.5 điểm) Cho biểu thức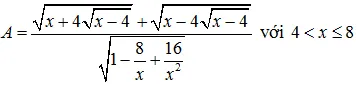

a) Rút gọn biểu thức A.

b) Tìm x nguyên để A có giá trị nguyên.

Câu 2: (2.5 điểm)

Số đo hai cạnh góc vuông của một tam giác là nghiệm của phương trình bậc hai (m – 2)x² – 2(m – 1)x + m = 0. Xác định m để số đo đường cao ứng với cạnh huyền của tam giác đã cho là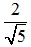

Câu 3: (3.0 điểm)

Cho hai đường tròn (O) và (O’) cắt nhau tại hai điểm A và B. Tiếp tuyến chung gần B của hai đường tròn lần lượt tiếp xúc (O) và (O’) tại C và D. Qua A kẻ đường thẳng song song CD cắt (O) và (O’) lần lượt tại M và N. Các đường thẳng BC, BD lần lượt cắt MN tại P và Q. Các đường thẳng CM, DN cắt nhau tại E. Chứng minh rằng:

a) Các đường thẳng AE và CD vuông góc nhau.

b) Tam giác EPQ cân.

Câu 4: (1.0 điểm) Cho x, y, z > 0 thỏa mãn: x² + y² + z² = 3. Chứng minh: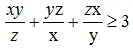

Câu 5: (1.0 điểm) Cho a, b, c, d là các số nguyên thỏa mãn: a⁵ + b⁵ = 4(c⁵ + d⁵)
Chứng minh rằng: a + b + c + d chia hết cho 5.

Download tài liệu để xem thêm chi tiết