| SỞ GIÁO DỤC VÀ ĐÀO TẠO NINH THUẬN Bạn đang đọc: Đề thi học sinh giỏi tỉnh Ninh Thuận môn Toán cấp THPT năm học 2011 – 2012 (Đề thi chính thức) |
KỲ THI CHỌN HỌC SINH GIỎI CẤP TỈNH NĂM HỌC 2011 – 2012 Khóa ngày: 17 / 11 / 2011 Môn thi: TOÁN Cấp: THPT Thời gian làm bài: 180 phút (Không kể thời gian phát đề) |
Bài 1 (5,0 điểm).
Tìm m để phương trình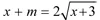 
có nghiệm
Bài 2 (4,0 điểm).
Có bao nhiêu số nguyên dương gồm 6 chữ số mà tích các chữ số của số này bằng 3500?
Bài 3 (5,0 điểm).
Cho góc vuông xOy và điểm A (A ≠ O) cố định trên đường phân giác Om của góc ấy. Một đường tròn (C ) thay đổi luôn đi qua hai điểm A, O cố định và cắt Ox tại M, cắt Oy tại N.
a) Chứng minh rằng khi đường tròn (C ) thay đổi thì tổng OM + ON có giá trị không đổi.
b) Tìm tập hợp các điểm I là trung điểm của đoạn thẳng MN khi đường tròn (C ) thay đổi.
Bài 4 (3,0 điểm).
Cho ba số dương a, b, c thỏa mãn điều kiện 2a + 3b + 4c = 1.
Chứng minh rằng: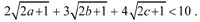 
Bài 5 (3,0 điểm).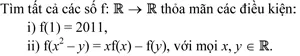
Download tài liệu để xem thêm chi tiết
